Πρώτη Μέρα, 13 Μαρτίου 2016, 11η τάξη.
Πρόβλημα 1. Σε σκακιστικό τουρνουά 12 συμμετεχόντων ο καθένας έπαιξε ακριβώς από μια παρτίδα με τους υπόλοιπους. Για την νίκη δινόταν 1 βαθμός, για την ισοπαλία ½ βαθμοί και για την ήττα 0 βαθμοί. Ο Βασίλης έχασε μόνο μια παρτίδα αλλά, κατέλαβε την τελευταία θέση, συγκεντρώνοντας τους λιγότερους βαθμούς. Ο Πέτρος κατέλαβε την πρώτη θέση, συγκεντρώνοντας τους περισσότερους βαθμούς. Πόσους βαθμούς υπολείφθηκε ο Βασίλης από τον Πέτρο;
Πρόβλημα 2. Υπάρχει τιμή του
 για την οποία ικανοποιείτε η ισότητα
για την οποία ικανοποιείτε η ισότητα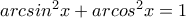 ;
;Πρόβλημα 3. Στο εσωτερικό τραπεζίου
 με βάσεις
με βάσεις  και
και  δίνονται σημεία
δίνονται σημεία  και
και  τέτοια, ώστε
τέτοια, ώστε  ,
,  και τα τετράπλευρα
και τα τετράπλευρα 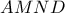 και
και  είναι εγγράψιμα. Να αποδείξετε, ότι η ευθεία
είναι εγγράψιμα. Να αποδείξετε, ότι η ευθεία  είναι παράλληλη των βάσεων του τραπεζίου.
είναι παράλληλη των βάσεων του τραπεζίου.Πρόβλημα 4. Στην εσπερίδα του αγγλικού συλλόγου συγκεντρώθηκαν
 μέλη του (
μέλη του ( 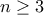 ). Σύμφωνα με την παράδοση του συλλόγου ο καθένας φέρνει το ποτό της προτίμησής του, σε ποσότητα που σκοπεύει να πιεί κατά την διάρκεια της εσπερίδας. Κατά τον κανονισμό του συλλόγου, οποιαδήποτε στιγμή οποιαδήποτε τρία μέλη του μπορούν να καθίσουν σε ένα τραπέζι και να πιούν το ποτό τους (ο καθένας το δικό του) σε οποιαδήποτε ποσότητα αλλά και οι τρεις την ίδια. Να αποδείξετε ότι, αναγκαία και ικανή συνθήκη, έτσι ώστε όλα τα μέλη κατά την διάρκεια της εσπερίδας να πιούν όλο το ποτό που έφεραν μαζί τους είναι: η ποσότητα του ποτού που έφερε ο καθένας να μην υπερβαίνει το ένα τρίτο της ποσότητας που συνολικά καταναλώθηκε.
). Σύμφωνα με την παράδοση του συλλόγου ο καθένας φέρνει το ποτό της προτίμησής του, σε ποσότητα που σκοπεύει να πιεί κατά την διάρκεια της εσπερίδας. Κατά τον κανονισμό του συλλόγου, οποιαδήποτε στιγμή οποιαδήποτε τρία μέλη του μπορούν να καθίσουν σε ένα τραπέζι και να πιούν το ποτό τους (ο καθένας το δικό του) σε οποιαδήποτε ποσότητα αλλά και οι τρεις την ίδια. Να αποδείξετε ότι, αναγκαία και ικανή συνθήκη, έτσι ώστε όλα τα μέλη κατά την διάρκεια της εσπερίδας να πιούν όλο το ποτό που έφεραν μαζί τους είναι: η ποσότητα του ποτού που έφερε ο καθένας να μην υπερβαίνει το ένα τρίτο της ποσότητας που συνολικά καταναλώθηκε. Πρόβλημα 5. Είναι άραγε δυνατόν με τέσσερα επίπεδα να κόψουμε κύβο ακμής 1 σε κομμάτια έτσι, ώστε για το καθένα από τα κομμάτια η απόσταση μεταξύ δυο οποιονδήποτε σημείων του να είναι α) μικρότερη του 4/5 ; β) μικρότερη του 4/7; . Υποθέτουμε ότι τα επίπεδα φέρονται ταυτόχρονα, ο κύβος και τα κομμάτια μένουν ακίνητα.
Πρόβλημα 6. Από την αριστερή όχθη στην δεξιά ενός ποταμού μεταφέρονται
 ιθαγενείς με την βοήθεια μιας βάρκας. Κάθε φορά στο ταξίδι προς την αριστερή όχθη επιβαίνουν δυο αλλά στην επιστροφή ένας. Αρχικά ο καθένας τους ήξερε από ένα ανέκδοτο, ο καθένας το δικό του. Στις όχθες δεν έλεγαν ανέκδοτα μεταξύ τους, αλλά κατά την διάρκεια του ταξιδιού στην βάρκα ο καθένας εξιστορούσε όλα τα ανέκδοτα που ήξερε εκείνη την χρονική στιγμή. Για κάθε φυσικό αριθμό
ιθαγενείς με την βοήθεια μιας βάρκας. Κάθε φορά στο ταξίδι προς την αριστερή όχθη επιβαίνουν δυο αλλά στην επιστροφή ένας. Αρχικά ο καθένας τους ήξερε από ένα ανέκδοτο, ο καθένας το δικό του. Στις όχθες δεν έλεγαν ανέκδοτα μεταξύ τους, αλλά κατά την διάρκεια του ταξιδιού στην βάρκα ο καθένας εξιστορούσε όλα τα ανέκδοτα που ήξερε εκείνη την χρονική στιγμή. Για κάθε φυσικό αριθμό  να βρείτε την ελάχιστη δυνατή τιμή του
να βρείτε την ελάχιστη δυνατή τιμή του  , για την οποία μπορεί να συμβεί το εξής: στο τέλος της μεταφοράς ο κάθε ιθαγενείς να ξέρει, εξαιρουμένου του δικού του, τουλάχιστον άλλα
, για την οποία μπορεί να συμβεί το εξής: στο τέλος της μεταφοράς ο κάθε ιθαγενείς να ξέρει, εξαιρουμένου του δικού του, τουλάχιστον άλλα  ανέκδοτα.
ανέκδοτα.Μέρα Δεύτερη, 19 Μαρτίου 2016, 11η τάξη.
Πρόβλημα 1. Να βρείτε τον μικρότερο φυσικό αριθμό το τετράγωνο του οποίου, στη δεκαδική μορφή, λήγει σε 2016.
Πρόβλημα 2. Δίνεται ζυγαριά δυο ζυγών, η οποία ισορροπεί, αν η διαφορά μάζας στους ζυγούς δεν υπερβαίνει το 1 κιλό. Καθώς και σταθμά μάζας
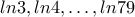 κιλών. Μπορούμε να τοποθετήσουμε όλα αυτά τα σταθμά στους ζυγούς της ζυγαριάς έτσι, ώστε η ζυγαριά να ισορροπεί;
κιλών. Μπορούμε να τοποθετήσουμε όλα αυτά τα σταθμά στους ζυγούς της ζυγαριάς έτσι, ώστε η ζυγαριά να ισορροπεί;Πρόβλημα 3. Είναι δυνατόν να διαλέξουμε
 κορυφές ενός κανονικού 14-γωνου έτσι, ώστε οποιοδήποτε τετράπλευρο με κορυφές αυτά τα σημεία, που έχει δυο πλευρές παράλληλες, να είναι ορθογώνιο αν α)
κορυφές ενός κανονικού 14-γωνου έτσι, ώστε οποιοδήποτε τετράπλευρο με κορυφές αυτά τα σημεία, που έχει δυο πλευρές παράλληλες, να είναι ορθογώνιο αν α)  , β)
, β) 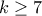 ;
;Πρόβλημα 4. Για κάποιο χρονικό διάστημα ένα παιδί έκανε βόλτα με το ποδήλατο, ακέραιο αριθμό φορών, την περίμετρο ενός σχολείου τετραγωνικού σχήματος προς την ίδια φορά με σταθερή κατά μέτρο ταχύτητα 10χμ/ώρα. Κατά το ίδιο χρονικό διάστημα ο πατέρας του παιδιού περπατούσε κατά την περίμετρο του σχολείου με ταχύτητα 5 χμ/ώρα αλλά μπορούσε και να αλλάξει φορά. Ο πατέρας έβλεπε το παιδί του μόνο εκείνες τις χρονικές στιγμές που βρισκόταν στην ίδια πλευρά του σχολείου. Θα μπορούσε να έβλεπε ο πατέρας το παιδί περισσότερο από το μισό της χρονικής διάρκειας της κοινής τους βόλτας;
Πρόβλημα 5. Για το μονικό πολυώνυμο
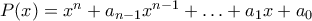
με πραγματικούς συντελεστές είναι γνωστό ότι για κάποιο φυσικό
 το πολυώνυμο
το πολυώνυμο 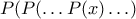 (
(  φορές)
φορές)έχει πραγματικές ρίζες και μάλιστα μόνο θετικές. Οποσδήποτε και το πολυώνυμο
 θα έχει πραγματικές ρίζες και μάλιστα μόνο θετικές;
θα έχει πραγματικές ρίζες και μάλιστα μόνο θετικές;Υγ. Στη δεύτερη μέρα συμμετέχουν μόνο οι μαθητές που έλυσαν τουλάχιστον δυο προλήματα την πρώτη.
Σημείωση: Σύμφωνα με την πηγή που είναι η επίσημη σελίδα της ολυμπιάδας εδώ. «Τα θέματα και οι λύσεις διατίθενται ελεύθερα για μη εμπορική χρήση (με επιθυμητή την αναφορά στην πηγή κατά την ανατύπωση)».

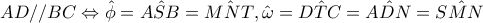 ,λόγω των εγγραψίμων τετραπλεύρων
,λόγω των εγγραψίμων τετραπλεύρων 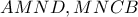
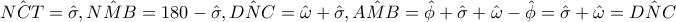
 είναι ίσα συνεπώς
είναι ίσα συνεπώς 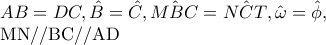
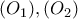 οι περιγγεγραμμένοι κύκλοι στα εγγράψιμα τετράπλευρα
οι περιγγεγραμμένοι κύκλοι στα εγγράψιμα τετράπλευρα 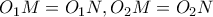
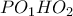 είναι μεσοκάθετος της
είναι μεσοκάθετος της 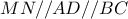
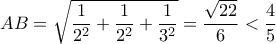
 είναι το 6, ο αριθμός που ζητάμε μπορεί να λήγει μόνο σε 4 ή 6.
είναι το 6, ο αριθμός που ζητάμε μπορεί να λήγει μόνο σε 4 ή 6.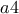 τότε το ψηφίο των δεκάδων του
τότε το ψηφίο των δεκάδων του 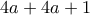 , άρα πρέπει
, άρα πρέπει  ή
ή  .
.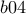 ή
ή  . Αποκλείεται η δεύτερη περίπτωση , γιατί τότε το ψηφίο των εκατοντάδων του
. Αποκλείεται η δεύτερη περίπτωση , γιατί τότε το ψηφίο των εκατοντάδων του 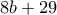 , που είναι περιττός (άθροισμα άρτιου και περιττού) άρα δεν μπορεί να είναι 0.
, που είναι περιττός (άθροισμα άρτιου και περιττού) άρα δεν μπορεί να είναι 0. .
.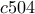 . Οι τιμές που μπορεί να πάρει το
. Οι τιμές που μπορεί να πάρει το  είναι 6 ή 9.
είναι 6 ή 9. .
.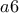 τότε το ψηφίο των δεκάδων του
τότε το ψηφίο των δεκάδων του 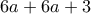 , άρα πρέπει
, άρα πρέπει 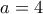 ή
ή  .
.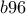 ή
ή 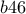 . Αποκλείεται η δεύτερη περίπτωση , γιατί τότε το ψηφίο των εκατοντάδων του
. Αποκλείεται η δεύτερη περίπτωση , γιατί τότε το ψηφίο των εκατοντάδων του 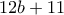 , που είναι περιττός (άθροισμα άρτιου και περιττού) άρα δεν μπορεί να είναι 0.
, που είναι περιττός (άθροισμα άρτιου και περιττού) άρα δεν μπορεί να είναι 0.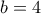 ή
ή  .
.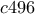 ή
ή 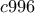 . Οι τιμές που μπορεί να πάρει το
. Οι τιμές που μπορεί να πάρει το  ή
ή ή
ή 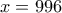 ή
ή 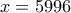 .
.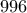 και είναι
και είναι  .
.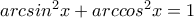 ;
;![\displaystyle{x \in \left[ { - 1,1} \right]} \displaystyle{x \in \left[ { - 1,1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/690ed97edebc27b407d2af36defb8457.png) τέτοιο, ώστε
τέτοιο, ώστε  Θέτουμε
Θέτουμε ![\displaystyle{u = \arcsin x \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]} \displaystyle{u = \arcsin x \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/3de18d189b4a1baac90e4ee80252b60b.png) και
και ![\displaystyle{v = \arccos x \in \left[ {0,\pi } \right].} \displaystyle{v = \arccos x \in \left[ {0,\pi } \right].}](/forum/ext/geomar/texintegr/latexrender/pictures/7e5a57b5409aece2c2878a9c15139d15.png) Τότε, είναι
Τότε, είναι 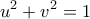
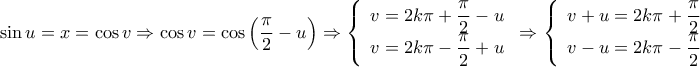
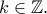
![\displaystyle{v + u \in \left[ { - \frac{\pi }{2},\frac{{3\pi }}{2}} \right]} \displaystyle{v + u \in \left[ { - \frac{\pi }{2},\frac{{3\pi }}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/2f9fff0ac66034a46a8ece6088789178.png) και
και ![\displaystyle{v - u \in \left[ { - \frac{\pi }{2},\frac{{3\pi }}{2}} \right]} \displaystyle{v - u \in \left[ { - \frac{\pi }{2},\frac{{3\pi }}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/bb09254d2a9d98a9bde1be37577c8cea.png) έχουμε τις περιπτώσεις
έχουμε τις περιπτώσεις 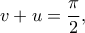
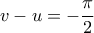 και
και 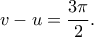 Καθεμιά, όμως από αυτές οδηγεί σε άτοπο, αφού αντιφάσκει (αντίστοιχα) με τις ανισότητες
Καθεμιά, όμως από αυτές οδηγεί σε άτοπο, αφού αντιφάσκει (αντίστοιχα) με τις ανισότητες 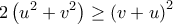 και
και 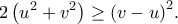
 παίκτες έπαιξαν
παίκτες έπαιξαν 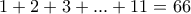 παρτίδες (από
παρτίδες (από  ο καθένας) και συγκέντρωσαν συνολικά
ο καθένας) και συγκέντρωσαν συνολικά  βαθμούς.
βαθμούς. βαθμούς (
βαθμούς ( από την ήττα και
από την ήττα και  ισοπαλίες), άρα οι
ισοπαλίες), άρα οι 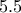 βαθμούς ο καθένας , οπότε Βασίλης και οι
βαθμούς ο καθένας , οπότε Βασίλης και οι 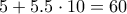 βαθμούς. Άρα για τον Πέτρο απομένουν το πολύ
βαθμούς. Άρα για τον Πέτρο απομένουν το πολύ 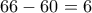 βαθμοί.
βαθμοί.  ακριβώς βαθμούς και ο Πέτρος
ακριβώς βαθμούς και ο Πέτρος  ακριβώς βαθμούς.
ακριβώς βαθμούς.  ) βαθμό.
) βαθμό.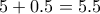 βαθμοί
βαθμοί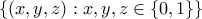 . Θεωρούμε το σύνολο
. Θεωρούμε το σύνολο 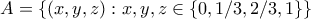 από
από  σημεία του κύβου. Είναι γνωστό ότι
σημεία του κύβου. Είναι γνωστό ότι  χωρία. Άρα
χωρία. Άρα  επίπεδα μπορούν να χωρίσουν τον κύβο το πολύ σε
επίπεδα μπορούν να χωρίσουν τον κύβο το πολύ σε  χωρία. Οπότε τουλάχιστον ένα από τα χωρία θα έχει τουλάχιστον
χωρία. Οπότε τουλάχιστον ένα από τα χωρία θα έχει τουλάχιστον  .
. το σύνολο αυτών των
το σύνολο αυτών των 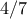 .
.  ή κατά
ή κατά 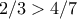 , άτοπο.
, άτοπο.  -συντεταγμένες και το πολύ δύο διαφορετικές
-συντεταγμένες και το πολύ δύο διαφορετικές  -συντεταγμένες.
-συντεταγμένες.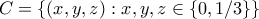 .
. σημεία του
σημεία του  , δύο από αυτά θα είναι αντιδιαμετρικά και άρα θα έχουν απόσταση
, δύο από αυτά θα είναι αντιδιαμετρικά και άρα θα έχουν απόσταση 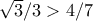 .
.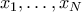 ανέκδοτα αντίστοιχα, τότε σε αυτήν την φάση δίνω την τιμή
ανέκδοτα αντίστοιχα, τότε σε αυτήν την φάση δίνω την τιμή 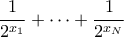
 .
. . Πράγματι έστω ότι στην διαδρομή μετακινήθηκαν άτομα που ξέρουν
. Πράγματι έστω ότι στην διαδρομή μετακινήθηκαν άτομα που ξέρουν  και
και  ανέκδοτα αντίστοιχα. Μπορούμε να υποθέσουμε ότι
ανέκδοτα αντίστοιχα. Μπορούμε να υποθέσουμε ότι  .
. τότε μετά την διαδρομή ξέρουν από
τότε μετά την διαδρομή ξέρουν από 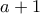 ανέκδοτα και η μείωση της τιμής είναι ακριβώς
ανέκδοτα και η μείωση της τιμής είναι ακριβώς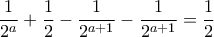
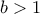 τότε η μείωση είναι αυστηρά μικρότερη από
τότε η μείωση είναι αυστηρά μικρότερη από
 διαδρομές στο τέλος η τιμή θα είναι τουλάχιστον
διαδρομές στο τέλος η τιμή θα είναι τουλάχιστον 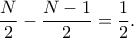
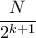
 και άρα
και άρα  .
. επιτυγχάνεται. Έστω π.χ. ότι
επιτυγχάνεται. Έστω π.χ. ότι  με
με  . Στην πρώτη διαδρομή πάνε ο
. Στην πρώτη διαδρομή πάνε ο  . Αυτοί τώρα ξέρουν από
. Αυτοί τώρα ξέρουν από  και ύστερα επιστρέφει ο
και ύστερα επιστρέφει ο  ώστε όλοι να ξέρουν από
ώστε όλοι να ξέρουν από  στην αντίπερα όχθη θα ξέρουν επαγωγικά από
στην αντίπερα όχθη θα ξέρουν επαγωγικά από  ανέκδοτα. Τώρα
ανέκδοτα. Τώρα  από αυτούς επιστρέφουν ένας ένας για να πάρουν από ένα από τους υπόλοιπους
από αυτούς επιστρέφουν ένας ένας για να πάρουν από ένα από τους υπόλοιπους  ιθαγενείς που ξέρουν από
ιθαγενείς που ξέρουν από 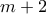 ανέκδοτα ενώ οι υπόλοιποι
ανέκδοτα ενώ οι υπόλοιποι 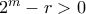 θα ξέρουν από
θα ξέρουν από