ΑΡΧΙΜΗΔΗΣ 2013-2014
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
ΑΡΧΙΜΗΔΗΣ 2013-2014
Έστω και καθυστερημένα, καλή επιτυχία στους διαγωνιζόμενους σήμερα!
Αν κάποιος διαθέτει τα θέματα ας τα ανεβάσει στο forum να τα δούμε! Ευχαριστώ!
Φιλικά,
Αχιλλέας
Αν κάποιος διαθέτει τα θέματα ας τα ανεβάσει στο forum να τα δούμε! Ευχαριστώ!
Φιλικά,
Αχιλλέας
- S.E.Louridas
- Δημοσιεύσεις: 5956
- Εγγραφή: Σάβ Μαρ 21, 2009 10:53 am
- Τοποθεσία: Aegaleo.
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
achilleas έγραψε: ...Αν κάποιος διαθέτει τα θέματα ας τα ανεβάσει στο forum να τα δούμε! Ευχαριστώ!
Φιλικά,
Αχιλλέας
Συμφωνώ απολύτως.
ΚΑΛΗ ΕΠΙΤΥΧΙΑ και από εμένα στους Διαγωνιζόμενους,
S.E.Louridas
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
1.Μιλώ, μόνο όταν έχω να πώ κάτι καλύτερο από την σιωπή (Πυθαγόρας).
2.Οι αξίες αντανακλώνται, Δεν επιβάλλονται.
3.Είναι Κορυφαία η κάθε στιγμή επίλυσης ενός Μαθηματικού προβλήματος.
-
Δημήτρης Τσιτσέλας
- Δημοσιεύσεις: 2
- Εγγραφή: Πέμ Ιαν 20, 2011 9:42 pm
-
kostas_zervos
- Δημοσιεύσεις: 1156
- Εγγραφή: Πέμ Μαρ 25, 2010 8:26 am
- Τοποθεσία: Κέρκυρα
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Πρόβλημα 1
Βρείτε όλα τα πολυώνυμα με πραγματικούς συντελεστές που ικανοποιούν την ισότητα
με πραγματικούς συντελεστές που ικανοποιούν την ισότητα  για κάθε
για κάθε  .
.


Για έχουμε
έχουμε  , για
, για 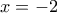 έχουμε
έχουμε  , για
, για  έχουμε
έχουμε  .
.
Άρα .
.
Τότε , άρα
, άρα

 για κάθε
για κάθε  , επομένως
, επομένως
 , άρα
, άρα  , δηλαδή
, δηλαδή  και
και  .
.
Άρα για κάθε
για κάθε  , επομένως
, επομένως
 .
.
Τότε όμως για κάθε
για κάθε  , δηλαδή το
, δηλαδή το 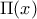 είναι σταθερό , έστω
είναι σταθερό , έστω 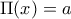 , άρα
, άρα
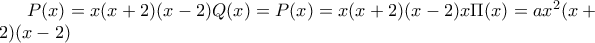 που επαληθεύει.
που επαληθεύει.
Βρείτε όλα τα πολυώνυμα
 με πραγματικούς συντελεστές που ικανοποιούν την ισότητα
με πραγματικούς συντελεστές που ικανοποιούν την ισότητα  για κάθε
για κάθε  .
.

Για
 έχουμε
έχουμε  , για
, για 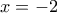 έχουμε
έχουμε  , για
, για  έχουμε
έχουμε  .
.Άρα
 .
.Τότε
 , άρα
, άρα
 για κάθε
για κάθε  , επομένως
, επομένως  , άρα
, άρα  , δηλαδή
, δηλαδή  και
και  .
.Άρα
 για κάθε
για κάθε  , επομένως
, επομένως  .
.Τότε όμως
 για κάθε
για κάθε  , δηλαδή το
, δηλαδή το 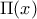 είναι σταθερό , έστω
είναι σταθερό , έστω 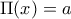 , άρα
, άρα 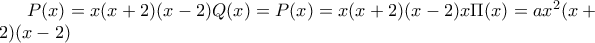 που επαληθεύει.
που επαληθεύει.
τελευταία επεξεργασία από kostas_zervos σε Σάβ Φεβ 22, 2014 2:52 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Κώστας Ζερβός
- ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
- Επιμελητής
- Δημοσιεύσεις: 4658
- Εγγραφή: Κυρ Μαρ 13, 2011 9:11 pm
- Τοποθεσία: Βρυξέλλες
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Πρόβλημα 4
Από το Θεώρημα του Pascal για το εκφυλισμένο εγγεγραμμένο στον κύκλο εξάγωνο
εξάγωνο  προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία
 είναι συνευθειακά. Από τους κύκλους
είναι συνευθειακά. Από τους κύκλους  προκύπτει ότι
προκύπτει ότι  ως
ως
το ριζικό τους κέντρο και προφανώς το μέσο της
το μέσο της  . Από το πλήρες τετράπλευρο
. Από το πλήρες τετράπλευρο 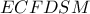 προκύπτει ότι η
προκύπτει ότι η  είναι η ευθεία
είναι η ευθεία  (με
(με  μέσο της
μέσο της  )
)
[attachment=0]1.png[/attachment]
και συνεπώς είναι το μέσο της
είναι το μέσο της  και με
και με  το μέσο της
το μέσο της  από το Θέωρημα της κεντρικής δέσμης
από το Θέωρημα της κεντρικής δέσμης  προκύπτει ότι
προκύπτει ότι

 εγγράψιμο και το ζητούμενο έχει αποδειχθεί.
εγγράψιμο και το ζητούμενο έχει αποδειχθεί.
Στάθης
Από το Θεώρημα του Pascal για το εκφυλισμένο εγγεγραμμένο στον κύκλο
 εξάγωνο
εξάγωνο  προκύπτει ότι τα σημεία
προκύπτει ότι τα σημεία  είναι συνευθειακά. Από τους κύκλους
είναι συνευθειακά. Από τους κύκλους  προκύπτει ότι
προκύπτει ότι  ως
ως το ριζικό τους κέντρο και προφανώς
 το μέσο της
το μέσο της  . Από το πλήρες τετράπλευρο
. Από το πλήρες τετράπλευρο 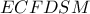 προκύπτει ότι η
προκύπτει ότι η  είναι η ευθεία
είναι η ευθεία  (με
(με  μέσο της
μέσο της  )
) [attachment=0]1.png[/attachment]
και συνεπώς
 είναι το μέσο της
είναι το μέσο της  και με
και με  το μέσο της
το μέσο της  από το Θέωρημα της κεντρικής δέσμης
από το Θέωρημα της κεντρικής δέσμης  προκύπτει ότι
προκύπτει ότι
 εγγράψιμο και το ζητούμενο έχει αποδειχθεί.
εγγράψιμο και το ζητούμενο έχει αποδειχθεί.Στάθης
- Συνημμένα
-
- 1.png (47.69 KiB) Προβλήθηκε 7357 φορές
τελευταία επεξεργασία από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ σε Σάβ Φεβ 22, 2014 4:40 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Τι περιμένετε λοιπόν ναρθεί , ποιόν καρτεράτε να σας σώσει.
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
-
Παύλος Μαραγκουδάκης
- Επιμελητής
- Δημοσιεύσεις: 1513
- Εγγραφή: Παρ Ιαν 30, 2009 1:45 pm
- Τοποθεσία: Πειραιάς
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Πρόβλημα 2
Βρείτε τις τιμές του ακέραιου για τις οποίες ο αριθμός
για τις οποίες ο αριθμός  ισούται με τον κύβο ρητού αριθμού.
ισούται με τον κύβο ρητού αριθμού.
Αν είναι ο Μ.Κ.Δ. των
είναι ο Μ.Κ.Δ. των  τότε ο
τότε ο  είναι διαιρέτης του
είναι διαιρέτης του 
Ας είναι όπου
όπου  ακέραιοι πρώτοι μεταξύ τους. Τότε
ακέραιοι πρώτοι μεταξύ τους. Τότε  και
και  Απαλείφοντας το
Απαλείφοντας το  βρίσκουμε
βρίσκουμε  με
με 
 Για
Για  είναι
είναι  Οι μόνοι κύβοι που διαφέρουν κατά
Οι μόνοι κύβοι που διαφέρουν κατά  είναι τα ζεύγη
είναι τα ζεύγη  και
και  Μόνο η πρώτη περίπτωση οδηγεί στη λύση
Μόνο η πρώτη περίπτωση οδηγεί στη λύση 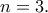
 Για
Για  είναι
είναι  Δεν υπάρχουν κύβοι που να διαφέρουν κατά
Δεν υπάρχουν κύβοι που να διαφέρουν κατά 
 Για
Για  είναι
είναι  Δεν υπάρχουν κύβοι που να διαφέρουν κατά
Δεν υπάρχουν κύβοι που να διαφέρουν κατά 
 Για
Για  είναι
είναι  Οι μόνοι κύβοι να διαφέρουν κατά
Οι μόνοι κύβοι να διαφέρουν κατά  είναι τα ζεύγη
είναι τα ζεύγη  και
και  που δεν οδηγούν σε λύση.
που δεν οδηγούν σε λύση.
Βρείτε τις τιμές του ακέραιου
 για τις οποίες ο αριθμός
για τις οποίες ο αριθμός  ισούται με τον κύβο ρητού αριθμού.
ισούται με τον κύβο ρητού αριθμού. Αν
 είναι ο Μ.Κ.Δ. των
είναι ο Μ.Κ.Δ. των  τότε ο
τότε ο  είναι διαιρέτης του
είναι διαιρέτης του 
Ας είναι
 όπου
όπου  ακέραιοι πρώτοι μεταξύ τους. Τότε
ακέραιοι πρώτοι μεταξύ τους. Τότε  και
και  Απαλείφοντας το
Απαλείφοντας το  βρίσκουμε
βρίσκουμε  με
με 
 Για
Για  είναι
είναι  Οι μόνοι κύβοι που διαφέρουν κατά
Οι μόνοι κύβοι που διαφέρουν κατά  είναι τα ζεύγη
είναι τα ζεύγη  και
και  Μόνο η πρώτη περίπτωση οδηγεί στη λύση
Μόνο η πρώτη περίπτωση οδηγεί στη λύση 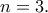
 Για
Για  είναι
είναι  Δεν υπάρχουν κύβοι που να διαφέρουν κατά
Δεν υπάρχουν κύβοι που να διαφέρουν κατά 
 Για
Για  είναι
είναι  Δεν υπάρχουν κύβοι που να διαφέρουν κατά
Δεν υπάρχουν κύβοι που να διαφέρουν κατά 
 Για
Για  είναι
είναι  Οι μόνοι κύβοι να διαφέρουν κατά
Οι μόνοι κύβοι να διαφέρουν κατά  είναι τα ζεύγη
είναι τα ζεύγη  και
και  που δεν οδηγούν σε λύση.
που δεν οδηγούν σε λύση.Στάλα τη στάλα το νερό το μάρμαρο τρυπά το,
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
εκείνο που μισεί κανείς γυρίζει κι αγαπά το.
-
nickthegreek
- Δημοσιεύσεις: 412
- Εγγραφή: Δευ Μαρ 01, 2010 2:07 pm
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Πολύ ωραία και φέτος τα προβλήματα. Εύχομαι καλή επιτυχία σε όλα τα παιδιά και στους γνωστούς μου που συμμετέχουν. Μου άρεσε το πρώτο πρόβλημα και θα παρουσιάσω μια διαφορετική σκέψη.
Παρατηρήστε ότι τα classic tricks με τα degrees των πολυωνύμων δεν λειτουργούν εδώ, καθώς ο βαθμός και των δύο πολυωνύμων εκατέρωθεν της ισότητας είναι , όπου
, όπου  . Άρα θέλουμε μια διαφορετική στρατηγική.
. Άρα θέλουμε μια διαφορετική στρατηγική.
Θέτω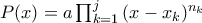 ,που είναι ουσιαστικά το πιο ισχυρό πράγμα που μπορούμε να θεωρήσουμε από το Polynomial condition, όπου οι ρίζες
,που είναι ουσιαστικά το πιο ισχυρό πράγμα που μπορούμε να θεωρήσουμε από το Polynomial condition, όπου οι ρίζες  .Τότε αν
.Τότε αν  τα πολυώνυμα
τα πολυώνυμα  αντιστοίχως είναι ίσα έχουμε ότι το άθροισμα των ριζών τους, counted with multiplicities, θα είναι το ίδιο.
αντιστοίχως είναι ίσα έχουμε ότι το άθροισμα των ριζών τους, counted with multiplicities, θα είναι το ίδιο.
Άρα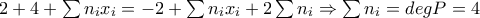 και άρα το πολυώνυμο είναι τετάρτου βαθμού. Τα υπόλοιπα είναι εύκολα.
και άρα το πολυώνυμο είναι τετάρτου βαθμού. Τα υπόλοιπα είναι εύκολα.
Παρατηρήστε ότι τα classic tricks με τα degrees των πολυωνύμων δεν λειτουργούν εδώ, καθώς ο βαθμός και των δύο πολυωνύμων εκατέρωθεν της ισότητας είναι
 , όπου
, όπου  . Άρα θέλουμε μια διαφορετική στρατηγική.
. Άρα θέλουμε μια διαφορετική στρατηγική.Θέτω
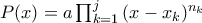 ,που είναι ουσιαστικά το πιο ισχυρό πράγμα που μπορούμε να θεωρήσουμε από το Polynomial condition, όπου οι ρίζες
,που είναι ουσιαστικά το πιο ισχυρό πράγμα που μπορούμε να θεωρήσουμε από το Polynomial condition, όπου οι ρίζες  .Τότε αν
.Τότε αν  τα πολυώνυμα
τα πολυώνυμα  αντιστοίχως είναι ίσα έχουμε ότι το άθροισμα των ριζών τους, counted with multiplicities, θα είναι το ίδιο.
αντιστοίχως είναι ίσα έχουμε ότι το άθροισμα των ριζών τους, counted with multiplicities, θα είναι το ίδιο.Άρα
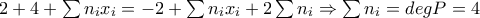 και άρα το πολυώνυμο είναι τετάρτου βαθμού. Τα υπόλοιπα είναι εύκολα.
και άρα το πολυώνυμο είναι τετάρτου βαθμού. Τα υπόλοιπα είναι εύκολα.Νίκος Αθανασίου
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
- Παναγιώτης Χ.
- Δημοσιεύσεις: 37
- Εγγραφή: Παρ Νοέμ 01, 2013 6:25 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Συγχαρητήρια σε όλους τους διαγωνιζόμενους και καλά αποτελέσματα  . Μήπως υπάρχουν οι λύσεις για τα θέματα του γυμνασίου (μικρών);
. Μήπως υπάρχουν οι λύσεις για τα θέματα του γυμνασίου (μικρών);
Παναγιώτης Χαλιμούρδας
- Παναγιώτης Χ.
- Δημοσιεύσεις: 37
- Εγγραφή: Παρ Νοέμ 01, 2013 6:25 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Τα θέματα των μικρών στο συνημμένο.
- Συνημμένα
-
- IMG_3306.JPG (120.49 KiB) Προβλήθηκε 7078 φορές
Παναγιώτης Χαλιμούρδας
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Για το 4ο των μικρών:
Έχουμε το σύνολο , το οποίο αποτελείται από τους αριθμούς που βάφουμε άσπρους, και
, το οποίο αποτελείται από τους αριθμούς που βάφουμε άσπρους, και  από τους αριθμούς που βάφουμε μαύρους.
από τους αριθμούς που βάφουμε μαύρους.
Χωρίς βλάβη της γενικότητας, τοποθετούμε το στο σύνολο
στο σύνολο  .
.
Έτσι όλοι οι άρτιοι πρέπει να βρίσκονται στο , αλλιώς ο μέγιστος κοινός διαιρέτης θα είναι τουλάχιστον
, αλλιώς ο μέγιστος κοινός διαιρέτης θα είναι τουλάχιστον  .
.
Ομοίως, θα ανήκουν στο οι αριθμοί
οι αριθμοί  , αφού ανήκουν στο
, αφού ανήκουν στο  οι αριθμοί
οι αριθμοί  .
.
Έτσι, όλοι οι αριθμοί εκτός από τους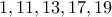 , ανήκουν στο
, ανήκουν στο  .
.
Επειδή το έχει ένα τουλάχιστον στοιχείο, οι
έχει ένα τουλάχιστον στοιχείο, οι  αριθμοί μπορούν να μοιραστούν στα δύο σύνολα με
αριθμοί μπορούν να μοιραστούν στα δύο σύνολα με  τρόπους (ή
τρόπους (ή  ).
).
Ομοίως αν θεωρήσουμε ότι το ανήκει στο
ανήκει στο  , θα έχουμε άλλους
, θα έχουμε άλλους  .
.
Έτσι έχουμε συνολικά τρόπους.
τρόπους.
*** Κατά τη γνώμη πολύ καλό πρόβλημα.
Έχουμε το σύνολο
 , το οποίο αποτελείται από τους αριθμούς που βάφουμε άσπρους, και
, το οποίο αποτελείται από τους αριθμούς που βάφουμε άσπρους, και  από τους αριθμούς που βάφουμε μαύρους.
από τους αριθμούς που βάφουμε μαύρους.Χωρίς βλάβη της γενικότητας, τοποθετούμε το
 στο σύνολο
στο σύνολο  .
.Έτσι όλοι οι άρτιοι πρέπει να βρίσκονται στο
 , αλλιώς ο μέγιστος κοινός διαιρέτης θα είναι τουλάχιστον
, αλλιώς ο μέγιστος κοινός διαιρέτης θα είναι τουλάχιστον  .
.Ομοίως, θα ανήκουν στο
 οι αριθμοί
οι αριθμοί  , αφού ανήκουν στο
, αφού ανήκουν στο  οι αριθμοί
οι αριθμοί  .
.Έτσι, όλοι οι αριθμοί εκτός από τους
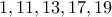 , ανήκουν στο
, ανήκουν στο  .
.Επειδή το
 έχει ένα τουλάχιστον στοιχείο, οι
έχει ένα τουλάχιστον στοιχείο, οι  αριθμοί μπορούν να μοιραστούν στα δύο σύνολα με
αριθμοί μπορούν να μοιραστούν στα δύο σύνολα με  τρόπους (ή
τρόπους (ή  ).
).Ομοίως αν θεωρήσουμε ότι το
 ανήκει στο
ανήκει στο  , θα έχουμε άλλους
, θα έχουμε άλλους  .
.Έτσι έχουμε συνολικά
 τρόπους.
τρόπους.*** Κατά τη γνώμη πολύ καλό πρόβλημα.
Τσιντσιλίδας Δημήτρης
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Μετά από την τετράωρη δοκιμασία, καθώς και το μάθημα διαρκείας μιάμισης ώρας που την ακολούθησε, επιτέλους έχω τη δυνατότητα να σχολιάσω, πιο ψύχραιμα τώρα, τα θέματα του λυκείου. Σαν γενική διαπίστωση, έχω να πω πως μου φάνηκαν αισθητά δυσκολότερα, συγκριτικά με τα τελευταία χρόνια. Έχω λύσει μόνο το πρώτο θέμα ολόκληρο, όπου βρήκα το ίδιο αποτέλεσμα με αυτό που προέκυψε στις λύσεις που δόθηκαν. Μονάχα, θα ήθελα να εκφράσω μία απορία. Για να δείξουμε στο τέλος πως πολυώνυμο που μένει είναι σταθερό, δεν πρέπει να αναφερθούμε και στο σύνολο των μιγαδικών; Συγκεκριμένα, διέκρινα δύο περιπτώσεις, να είναι το μηδενικό πολυώνυμο (προφανής λύση) και είναι μη σταθερό. Στη δεύτερη περίπτωση κατέληξα σε σχέση της μορφής  . Εκεί, το δικαιολόγησα λέγοντας πως εάν έχει ρίζα έναν μιγαδικό αριθμό θα έχει ως ρίζα οποιοδήποτε μιγαδικό της μορφής
. Εκεί, το δικαιολόγησα λέγοντας πως εάν έχει ρίζα έναν μιγαδικό αριθμό θα έχει ως ρίζα οποιοδήποτε μιγαδικό της μορφής  , πράγμα αδύνατο για ένα μη μηδενικό πολυώνυμο, γεγονός που μας εξασφαλίζει πως
, πράγμα αδύνατο για ένα μη μηδενικό πολυώνυμο, γεγονός που μας εξασφαλίζει πως  . Έτσι κατέληξα πως λύση αποτελούν τα πολυώνυμα της οικογένειας
. Έτσι κατέληξα πως λύση αποτελούν τα πολυώνυμα της οικογένειας  , όπου για
, όπου για  έχουμε το μηδενικό πολυώνυμο της πρώτης περίπτωσης.
έχουμε το μηδενικό πολυώνυμο της πρώτης περίπτωσης.
Τώρα, όσον αφορά στα υπόλοιπα θέματα, ομολογώ πως αντιμετώπησα δυσκολίες. Η θεωρία αριθμών δεν είναι το φόρτε μου, όποτε δεν μπόρω να αντιμετωπίσω το θέμα στο σύνολό του. Μόνο μερικές τυχαίες σκέψεις έγραψα, οι οποίες αμφιβάλλω όμως εάν μου δώσουν μονάδες. Το τρίτο το βρήκα αρκετά ενδιαφέρον, και γι' αυτό το πάλεψα και νομίζω πως μέχρι εκεί που έγραψα ήταν σωστές οι ενέργειές μου. Συγκεκριμένα είπα πως πρέπει , και αφού
, και αφού  έχουμε
έχουμε  , το οποίο δίνει
, το οποίο δίνει  . Εκεί σταμάτησα. Δεν μπόρεσα να προχωρήσω παραπέρα, αλλά θα με ενδιέφερε να δω την πλήρη λύση.
. Εκεί σταμάτησα. Δεν μπόρεσα να προχωρήσω παραπέρα, αλλά θα με ενδιέφερε να δω την πλήρη λύση.
Πάμε τώρα και στη γεωμετρία. Ομολογώ πως εκεί περίμενα πως κατάφερνα κάτι, καθώς είχα ασχοληθεί παραπάνω με τη γεωμετρία τον τελευταίο καιρό, ελπίζοντας πως με την εξάσκηση θα βελτιωνόμουν. Οι δε επιδόσεις μου τόσο στο πρόβλημα του Θαλή, όσο και σε εκείνο του Ευκλείδη ήταν πολύ καλές. Παρ' όλα αυτά όμως δεν στάθηκα τυχερός, καθώς το πρόβλημα απ' ό,τι φαίνεται ήταν αισθητά απαιτητικότερο από αντίστοιχα των προηγούμενων ετών, με συνέπεια να περιοριστώ σε κάποιες λίγες σκέψεις, που πιστεύω τουλάχιστον πως είναι στη σωστή κατεύθυνση. Πάντως η αύξηση της δυσκολίας είναι ένα στοιχείο θεωρώ θετικό, καθώς ένα τέταρτο θέμα γεωμετρίας πρέπει προσεγγίζει το επίπεδο δυσκολίας των προβλημάτων των ολυμπιάδων και να απευθύνεται μόνος στους άριστους, που έχουν ιδιαίτερη σχέση με το αντικείμενο. Θα με ενδιέφερε, ωστόσο, να δω μία προσέγγιση του θέματος με πιο στοιχειώδη μέσα, μιας και αμφιβάλλω εάν ο κατασκευαστής του προβλήματος είχε στο νου του λύση με θεωρήματα όπως αυτά που χρησιμοποιεί ο κύριος Κούτρας στη λύση του.
Γενικά, με υπολογίζω κοντά στο 1,5 θέμα, αν και πιστεύω πως θα μπορούσα να είχα πάει και καλύτερα...
 . Εκεί, το δικαιολόγησα λέγοντας πως εάν έχει ρίζα έναν μιγαδικό αριθμό θα έχει ως ρίζα οποιοδήποτε μιγαδικό της μορφής
. Εκεί, το δικαιολόγησα λέγοντας πως εάν έχει ρίζα έναν μιγαδικό αριθμό θα έχει ως ρίζα οποιοδήποτε μιγαδικό της μορφής  , πράγμα αδύνατο για ένα μη μηδενικό πολυώνυμο, γεγονός που μας εξασφαλίζει πως
, πράγμα αδύνατο για ένα μη μηδενικό πολυώνυμο, γεγονός που μας εξασφαλίζει πως  . Έτσι κατέληξα πως λύση αποτελούν τα πολυώνυμα της οικογένειας
. Έτσι κατέληξα πως λύση αποτελούν τα πολυώνυμα της οικογένειας  , όπου για
, όπου για  έχουμε το μηδενικό πολυώνυμο της πρώτης περίπτωσης.
έχουμε το μηδενικό πολυώνυμο της πρώτης περίπτωσης.Τώρα, όσον αφορά στα υπόλοιπα θέματα, ομολογώ πως αντιμετώπησα δυσκολίες. Η θεωρία αριθμών δεν είναι το φόρτε μου, όποτε δεν μπόρω να αντιμετωπίσω το θέμα στο σύνολό του. Μόνο μερικές τυχαίες σκέψεις έγραψα, οι οποίες αμφιβάλλω όμως εάν μου δώσουν μονάδες. Το τρίτο το βρήκα αρκετά ενδιαφέρον, και γι' αυτό το πάλεψα και νομίζω πως μέχρι εκεί που έγραψα ήταν σωστές οι ενέργειές μου. Συγκεκριμένα είπα πως πρέπει
 , και αφού
, και αφού  έχουμε
έχουμε  , το οποίο δίνει
, το οποίο δίνει  . Εκεί σταμάτησα. Δεν μπόρεσα να προχωρήσω παραπέρα, αλλά θα με ενδιέφερε να δω την πλήρη λύση.
. Εκεί σταμάτησα. Δεν μπόρεσα να προχωρήσω παραπέρα, αλλά θα με ενδιέφερε να δω την πλήρη λύση.Πάμε τώρα και στη γεωμετρία. Ομολογώ πως εκεί περίμενα πως κατάφερνα κάτι, καθώς είχα ασχοληθεί παραπάνω με τη γεωμετρία τον τελευταίο καιρό, ελπίζοντας πως με την εξάσκηση θα βελτιωνόμουν. Οι δε επιδόσεις μου τόσο στο πρόβλημα του Θαλή, όσο και σε εκείνο του Ευκλείδη ήταν πολύ καλές. Παρ' όλα αυτά όμως δεν στάθηκα τυχερός, καθώς το πρόβλημα απ' ό,τι φαίνεται ήταν αισθητά απαιτητικότερο από αντίστοιχα των προηγούμενων ετών, με συνέπεια να περιοριστώ σε κάποιες λίγες σκέψεις, που πιστεύω τουλάχιστον πως είναι στη σωστή κατεύθυνση. Πάντως η αύξηση της δυσκολίας είναι ένα στοιχείο θεωρώ θετικό, καθώς ένα τέταρτο θέμα γεωμετρίας πρέπει προσεγγίζει το επίπεδο δυσκολίας των προβλημάτων των ολυμπιάδων και να απευθύνεται μόνος στους άριστους, που έχουν ιδιαίτερη σχέση με το αντικείμενο. Θα με ενδιέφερε, ωστόσο, να δω μία προσέγγιση του θέματος με πιο στοιχειώδη μέσα, μιας και αμφιβάλλω εάν ο κατασκευαστής του προβλήματος είχε στο νου του λύση με θεωρήματα όπως αυτά που χρησιμοποιεί ο κύριος Κούτρας στη λύση του.
Γενικά, με υπολογίζω κοντά στο 1,5 θέμα, αν και πιστεύω πως θα μπορούσα να είχα πάει και καλύτερα...
τελευταία επεξεργασία από ArgirisM σε Σάβ Φεβ 22, 2014 5:26 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Αν κάτι μπορεί να πάει στραβά, θα πάει!
Νόμος του Μέρφυ
Νόμος του Μέρφυ
-
panagiotis99
- Δημοσιεύσεις: 133
- Εγγραφή: Δευ Φεβ 04, 2013 8:24 pm
- Τοποθεσία: Αθηνα
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Στο τέταρτο θέμα έχω δωσει την ιδια λυση με τον Δημήτρη.
Τώρα για το τρίτο θέμα των μικρών
Αν κάνουμε απαλοιφή παρονομαστών και στις τρεις σχέσεις και μετά τις προσθέσουμε κατα μέλη και μετά απο λίγες πράξεις καταλήγουμε στην ισότητα

Η λύση χ=y=z=0 απορριπτεται διότι δεν ικανοποιούνται οι περιορισμοί
αρα έχουμε χyz = -1
Τέλος ισχυεί για κάθε τριάδα πραγματικών αριθμών που έχουν γινόμενο -1
Τώρα για το τρίτο θέμα των μικρών
Αν κάνουμε απαλοιφή παρονομαστών και στις τρεις σχέσεις και μετά τις προσθέσουμε κατα μέλη και μετά απο λίγες πράξεις καταλήγουμε στην ισότητα

Η λύση χ=y=z=0 απορριπτεται διότι δεν ικανοποιούνται οι περιορισμοί
αρα έχουμε χyz = -1
Τέλος ισχυεί για κάθε τριάδα πραγματικών αριθμών που έχουν γινόμενο -1
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Εγώ την έβαλα ως λύση αφού ορίζεται το κλάσμαpanagiotis99 έγραψε:Στο τέταρτο θέμα έχω δωσει την ιδια λυση με τον Δημήτρη.
Τώρα για το τρίτο θέμα των μικρών
Αν κάνουμε απαλοιφή παρονομαστών και στις τρεις σχέσεις και μετά τις προσθέσουμε κατα μέλη και μετά απο λίγες πράξεις καταλήγουμε στην ισότητα
Η λύση χ=y=z=0 απορριπτεται διότι δεν ικανοποιούνται οι περιορισμοί
αρα έχουμε χyz = -1
Τέλος ισχυεί για κάθε τριάδα πραγματικών αριθμών που έχουν γινόμενο -1
 . Κάνω λάθος;;
. Κάνω λάθος;;Τσιντσιλίδας Δημήτρης
-
nickthegreek
- Δημοσιεύσεις: 412
- Εγγραφή: Δευ Μαρ 01, 2010 2:07 pm
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Επειδή πέρασε πολύς καιρός από τότε που ασχολήθηκα με ευκλείδεια γεωμετρία και ομολογουμένως μου έλειψε , ας δούμε και μια πιο στοιχειώδη προσέγγιση για το τέταρτο θέμα, μόνο με κυνήγι γωνιών και αναλογίες.
Αρχικά παρατηρώ ότι οι γωνίες είναι ίσες, διότι
είναι ίσες, διότι  από τις εφαπτόμενες ευθείες και επίσης
από τις εφαπτόμενες ευθείες και επίσης  από το εγγράψιμο. Αφαιρώ κατά ζεύγη και φτάνω στο ζητούμενο.
από το εγγράψιμο. Αφαιρώ κατά ζεύγη και φτάνω στο ζητούμενο.
Στόχος μου είναι να δείξω ότι τα τρίγωνα είναι όμοια , από όπου το ζητούμενο προκύπτει κατευθείαν. Για να το καταφέρω αυτό, εφ' όσον έχω το ένα ζεύγος γωνιών ίσα από το προηγούμενο επιχείρημα, προσπαθώ να δείξω ότι και οι αντίστοιχες πλευρές είναι ανάλογες. Αν G το σημείο τομής της
είναι όμοια , από όπου το ζητούμενο προκύπτει κατευθείαν. Για να το καταφέρω αυτό, εφ' όσον έχω το ένα ζεύγος γωνιών ίσα από το προηγούμενο επιχείρημα, προσπαθώ να δείξω ότι και οι αντίστοιχες πλευρές είναι ανάλογες. Αν G το σημείο τομής της  με τον κύκλο
με τον κύκλο  , τότε από δύναμη σημείου αρκεί να δείξω ότι
, τότε από δύναμη σημείου αρκεί να δείξω ότι  .
.
Ας μου επιτραπεί σε αυτό το σημείο μια γενική συμβουλή-σχόλιο για τον τρόπο αντιμετώπισης αυτών των γεωμετρικών προβλημάτων σε hide:
Φέρω την . Τα τρίγωνα
. Τα τρίγωνα  είναι ίσα διότι έχουν δύο γωνίες ίσες και μια πλευρά κοινή.
είναι ίσα διότι έχουν δύο γωνίες ίσες και μια πλευρά κοινή.
Αρχικά παρατηρώ ότι οι γωνίες
 είναι ίσες, διότι
είναι ίσες, διότι  από τις εφαπτόμενες ευθείες και επίσης
από τις εφαπτόμενες ευθείες και επίσης  από το εγγράψιμο. Αφαιρώ κατά ζεύγη και φτάνω στο ζητούμενο.
από το εγγράψιμο. Αφαιρώ κατά ζεύγη και φτάνω στο ζητούμενο. Στόχος μου είναι να δείξω ότι τα τρίγωνα
 είναι όμοια , από όπου το ζητούμενο προκύπτει κατευθείαν. Για να το καταφέρω αυτό, εφ' όσον έχω το ένα ζεύγος γωνιών ίσα από το προηγούμενο επιχείρημα, προσπαθώ να δείξω ότι και οι αντίστοιχες πλευρές είναι ανάλογες. Αν G το σημείο τομής της
είναι όμοια , από όπου το ζητούμενο προκύπτει κατευθείαν. Για να το καταφέρω αυτό, εφ' όσον έχω το ένα ζεύγος γωνιών ίσα από το προηγούμενο επιχείρημα, προσπαθώ να δείξω ότι και οι αντίστοιχες πλευρές είναι ανάλογες. Αν G το σημείο τομής της  με τον κύκλο
με τον κύκλο  , τότε από δύναμη σημείου αρκεί να δείξω ότι
, τότε από δύναμη σημείου αρκεί να δείξω ότι  .
.Ας μου επιτραπεί σε αυτό το σημείο μια γενική συμβουλή-σχόλιο για τον τρόπο αντιμετώπισης αυτών των γεωμετρικών προβλημάτων σε hide:
Φέρω την
 . Τα τρίγωνα
. Τα τρίγωνα  είναι ίσα διότι έχουν δύο γωνίες ίσες και μια πλευρά κοινή.
είναι ίσα διότι έχουν δύο γωνίες ίσες και μια πλευρά κοινή.Νίκος Αθανασίου
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
- Παναγιώτης Χ.
- Δημοσιεύσεις: 37
- Εγγραφή: Παρ Νοέμ 01, 2013 6:25 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Η δική μου λύση για το θέμα 2 των μικρών:

Για έχουμε:
έχουμε:  \displaystyle{5=m^3+3m^2+m \Leftrightarrow}
\displaystyle{5=m^3+3m^2+m \Leftrightarrow} . Άρα
. Άρα  ή
ή 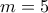 (άτοπο). Άρα
(άτοπο). Άρα  .
.
Για καταλήγουμε σε άτοπο.
καταλήγουμε σε άτοπο.

Για
 έχουμε:
έχουμε:  \displaystyle{5=m^3+3m^2+m \Leftrightarrow}
\displaystyle{5=m^3+3m^2+m \Leftrightarrow} . Άρα
. Άρα  ή
ή 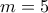 (άτοπο). Άρα
(άτοπο). Άρα  .
.Για
 καταλήγουμε σε άτοπο.
καταλήγουμε σε άτοπο.Παναγιώτης Χαλιμούρδας
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Καλησπέρα...να ρωτήσω ξέρει κανείς ποτε θα ανακοινωθούν οι επιτυχόντες...??? 
- Παναγιώτης Χ.
- Δημοσιεύσεις: 37
- Εγγραφή: Παρ Νοέμ 01, 2013 6:25 pm
- Τοποθεσία: Θεσσαλονίκη
- Επικοινωνία:
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Κι εγώ αυτό περιμένω... Αλλά πρέπει να δώσουμε και λίγο χρόνο στην ΕΜΕ γιατί διορθώνουν όλη την ημέρα!dimfous4 έγραψε:Καλησπέρα...να ρωτήσω ξέρει κανείς πότε θα ανακοινωθούν οι επιτυχόντες...???
Παναγιώτης Χαλιμούρδας
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
ok...απλώς αν πλώς αν μπoρεi κάποιος μολις βγουν να βάλει to λινκ ή να μας ειΠαναγιώτης Χ. έγραψε:Κι εγώ αυτό περιμένω... Αλλά πρέπει να δώσουμε και λίγο χρόνο στην ΕΜΕ γιατί διορθώνουν όλη την ημέρα!dimfous4 έγραψε:Καλησπέρα...να ρωτήσω ξέρει κανείς πότε θα ανακοινωθούν οι επιτυχόντες...???
-
nickthegreek
- Δημοσιεύσεις: 412
- Εγγραφή: Δευ Μαρ 01, 2010 2:07 pm
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
To 3o πρόβλημα είναι κατά τη γνώμη μου δυνατό-δύσκολο και η ύπαρξή του στον διαγωνισμό θα ξεχωρίσει τους μαθητές που είχαν εξαιρετική επίδοση από αυτούς που είχαν άριστη επίδοση. Ας δούμε μια λύση.
Έστω τέτοιο ώστε
τέτοιο ώστε 
Από εδώ συνάγουμε ότι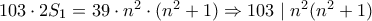 . Η κρίσιμη παρατήρηση σε αυτό το σημείο του προβλήματος είναι ότι το
. Η κρίσιμη παρατήρηση σε αυτό το σημείο του προβλήματος είναι ότι το  δεν είναι τετραγωνικό κατάλοιπο
δεν είναι τετραγωνικό κατάλοιπο  , διότι
, διότι  (γνωστό θεώρημα στη θεωρία αριθμών, όποιος ενδιαφέρεται ας διαβάσει για το σύμβολο Legendre εδώ: http://en.wikipedia.org/wiki/Legendre_symbol). Κατά συνέπεια
(γνωστό θεώρημα στη θεωρία αριθμών, όποιος ενδιαφέρεται ας διαβάσει για το σύμβολο Legendre εδώ: http://en.wikipedia.org/wiki/Legendre_symbol). Κατά συνέπεια  και άρα
και άρα 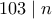 , αφού ο
, αφού ο  είναι πρώτος. Τελικά , λαμβάνουμε ένα necessary condition:
είναι πρώτος. Τελικά , λαμβάνουμε ένα necessary condition:

Iσχυρίζομαι ότι για κάθε τέτοιο υπάρχει μια κατάλληλη τοποθέτηση. Εδώ παρατηρούμε ότι ήδη η σκακιέρα μας είναι πολύ μεγάλη! Συνεπώς, μια κατασκευαστική απόδειξη θα ήταν πολύ δύσκολη. Θα προσπαθήσουμε λοιπόν να αποδείξουμε έμμεσα ότι μια τέτοια τοποθέτηση υπάρχει. Ξαναγράφουμε το πρόβλημά μας στην εξής ισοδύναμη μορφή:
υπάρχει μια κατάλληλη τοποθέτηση. Εδώ παρατηρούμε ότι ήδη η σκακιέρα μας είναι πολύ μεγάλη! Συνεπώς, μια κατασκευαστική απόδειξη θα ήταν πολύ δύσκολη. Θα προσπαθήσουμε λοιπόν να αποδείξουμε έμμεσα ότι μια τέτοια τοποθέτηση υπάρχει. Ξαναγράφουμε το πρόβλημά μας στην εξής ισοδύναμη μορφή:
" Έχουμε τους αριθμούς . Να αποδείξετε ότι υπάρχουν
. Να αποδείξετε ότι υπάρχουν 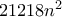 διαφορετικοί ανά δύο αριθμοί οι οποίοι έχουν άθροισμα
διαφορετικοί ανά δύο αριθμοί οι οποίοι έχουν άθροισμα  " . Θέτω
" . Θέτω 
Ας δούμε ποια είναι η ελάχιστη και η μέγιστη τιμή που μπορεί να έχουμε. Η ελάχιστη είναι και η μέγιστη είναι
και η μέγιστη είναι  . Παρατηρούμε ότι η τιμή
. Παρατηρούμε ότι η τιμή  είναι ανάμεσα στη μέγιστη και στην ελάχιστη τιμή (για να το δω αυτό, διαιρώ τη μέγιστη και ελάχιστη τιμή με
είναι ανάμεσα στη μέγιστη και στην ελάχιστη τιμή (για να το δω αυτό, διαιρώ τη μέγιστη και ελάχιστη τιμή με  και παρατηρώ ότι τα αντίστοιχα κλάσματα είναι πολύ κοντά στο
και παρατηρώ ότι τα αντίστοιχα κλάσματα είναι πολύ κοντά στο  αντίστοιχα) .
αντίστοιχα) .
Ισχυρίζομαι ότι κάθε ακέραιος αριθμός ανάμεσα στα είναι εφικτός ως άθροισμα. Ας υποθέσουμε ότι έχω
είναι εφικτός ως άθροισμα. Ας υποθέσουμε ότι έχω 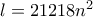 αριθμούς
αριθμούς
 με
με  . Θα ξεκινήσω από την
. Θα ξεκινήσω από την  άδα
άδα  και θα αποδείξω επαγωγικά ότι μπορώ να πετύχω μια
και θα αποδείξω επαγωγικά ότι μπορώ να πετύχω μια  άδα με άθροισμα κατά ένα μεγαλύτερο της προηγούμενης.
άδα με άθροισμα κατά ένα μεγαλύτερο της προηγούμενης.
Διαλέγω το . Αν
. Αν  τότε παίρνω την
τότε παίρνω την  άδα
άδα  . Αν
. Αν  τότε κοιτάζω το
τότε κοιτάζω το  κ.ο.κ. Αν δεν μπορώ να κουνήσω κανένα στοιχείο σημαίνει ότι έχω ήδη φτάσει στη μέγιστη τιμή , οπότε τελείωσα.
κ.ο.κ. Αν δεν μπορώ να κουνήσω κανένα στοιχείο σημαίνει ότι έχω ήδη φτάσει στη μέγιστη τιμή , οπότε τελείωσα.
Το ζητούμενο έπεται.
Έστω
 τέτοιο ώστε
τέτοιο ώστε 
Από εδώ συνάγουμε ότι
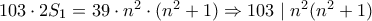 . Η κρίσιμη παρατήρηση σε αυτό το σημείο του προβλήματος είναι ότι το
. Η κρίσιμη παρατήρηση σε αυτό το σημείο του προβλήματος είναι ότι το  δεν είναι τετραγωνικό κατάλοιπο
δεν είναι τετραγωνικό κατάλοιπο  , διότι
, διότι  (γνωστό θεώρημα στη θεωρία αριθμών, όποιος ενδιαφέρεται ας διαβάσει για το σύμβολο Legendre εδώ: http://en.wikipedia.org/wiki/Legendre_symbol). Κατά συνέπεια
(γνωστό θεώρημα στη θεωρία αριθμών, όποιος ενδιαφέρεται ας διαβάσει για το σύμβολο Legendre εδώ: http://en.wikipedia.org/wiki/Legendre_symbol). Κατά συνέπεια  και άρα
και άρα 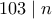 , αφού ο
, αφού ο  είναι πρώτος. Τελικά , λαμβάνουμε ένα necessary condition:
είναι πρώτος. Τελικά , λαμβάνουμε ένα necessary condition:
Iσχυρίζομαι ότι για κάθε τέτοιο
 υπάρχει μια κατάλληλη τοποθέτηση. Εδώ παρατηρούμε ότι ήδη η σκακιέρα μας είναι πολύ μεγάλη! Συνεπώς, μια κατασκευαστική απόδειξη θα ήταν πολύ δύσκολη. Θα προσπαθήσουμε λοιπόν να αποδείξουμε έμμεσα ότι μια τέτοια τοποθέτηση υπάρχει. Ξαναγράφουμε το πρόβλημά μας στην εξής ισοδύναμη μορφή:
υπάρχει μια κατάλληλη τοποθέτηση. Εδώ παρατηρούμε ότι ήδη η σκακιέρα μας είναι πολύ μεγάλη! Συνεπώς, μια κατασκευαστική απόδειξη θα ήταν πολύ δύσκολη. Θα προσπαθήσουμε λοιπόν να αποδείξουμε έμμεσα ότι μια τέτοια τοποθέτηση υπάρχει. Ξαναγράφουμε το πρόβλημά μας στην εξής ισοδύναμη μορφή:" Έχουμε τους αριθμούς
 . Να αποδείξετε ότι υπάρχουν
. Να αποδείξετε ότι υπάρχουν 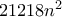 διαφορετικοί ανά δύο αριθμοί οι οποίοι έχουν άθροισμα
διαφορετικοί ανά δύο αριθμοί οι οποίοι έχουν άθροισμα  " . Θέτω
" . Θέτω 
Ας δούμε ποια είναι η ελάχιστη και η μέγιστη τιμή που μπορεί να έχουμε. Η ελάχιστη είναι
 και η μέγιστη είναι
και η μέγιστη είναι  . Παρατηρούμε ότι η τιμή
. Παρατηρούμε ότι η τιμή  είναι ανάμεσα στη μέγιστη και στην ελάχιστη τιμή (για να το δω αυτό, διαιρώ τη μέγιστη και ελάχιστη τιμή με
είναι ανάμεσα στη μέγιστη και στην ελάχιστη τιμή (για να το δω αυτό, διαιρώ τη μέγιστη και ελάχιστη τιμή με  και παρατηρώ ότι τα αντίστοιχα κλάσματα είναι πολύ κοντά στο
και παρατηρώ ότι τα αντίστοιχα κλάσματα είναι πολύ κοντά στο  αντίστοιχα) .
αντίστοιχα) . Ισχυρίζομαι ότι κάθε ακέραιος αριθμός ανάμεσα στα
 είναι εφικτός ως άθροισμα. Ας υποθέσουμε ότι έχω
είναι εφικτός ως άθροισμα. Ας υποθέσουμε ότι έχω 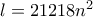 αριθμούς
αριθμούς με
με  . Θα ξεκινήσω από την
. Θα ξεκινήσω από την  άδα
άδα  και θα αποδείξω επαγωγικά ότι μπορώ να πετύχω μια
και θα αποδείξω επαγωγικά ότι μπορώ να πετύχω μια  άδα με άθροισμα κατά ένα μεγαλύτερο της προηγούμενης.
άδα με άθροισμα κατά ένα μεγαλύτερο της προηγούμενης.Διαλέγω το
 . Αν
. Αν  τότε παίρνω την
τότε παίρνω την  άδα
άδα  . Αν
. Αν  τότε κοιτάζω το
τότε κοιτάζω το  κ.ο.κ. Αν δεν μπορώ να κουνήσω κανένα στοιχείο σημαίνει ότι έχω ήδη φτάσει στη μέγιστη τιμή , οπότε τελείωσα.
κ.ο.κ. Αν δεν μπορώ να κουνήσω κανένα στοιχείο σημαίνει ότι έχω ήδη φτάσει στη μέγιστη τιμή , οπότε τελείωσα. Το ζητούμενο έπεται.
τελευταία επεξεργασία από nickthegreek σε Κυρ Φεβ 23, 2014 1:28 pm, έχει επεξεργασθεί 4 φορές συνολικά.
Νίκος Αθανασίου
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
Μεταδιδακτορικός ερευνητής, τμήμα μαθηματικών- Πανεπιστήμιο Κρήτης
Re: ΑΡΧΙΜΗΔΗΣ 2013-2014
Θερμά συγχαρητήρια σε όσους συμμετείχαν και σε όσους διακρίθηκαν.
Τα αποτελέσματα ανακοινώθηκαν.
Φιλικά,
Αχιλλέας
Τα αποτελέσματα ανακοινώθηκαν.
Φιλικά,
Αχιλλέας
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες

 δεν εμπλέκεται πλέον άμεσα στην άσκηση, οπότε στον διαγωνισμό καλό είναι να γίνει σε αυτό το σημείο ένα νέο σχήμα, μόνο με τα απαραίτητα σημεία
δεν εμπλέκεται πλέον άμεσα στην άσκηση, οπότε στον διαγωνισμό καλό είναι να γίνει σε αυτό το σημείο ένα νέο σχήμα, μόνο με τα απαραίτητα σημεία  . Εξάλλου στη γεωμετρία ο στόχος είναι μέσα στο χαοτικό διάγραμμα να βρεις ποια είναι τα "connected" κατά κάποιον τρόπο μικρότερα σχήματα και να εστιάσεις σε αυτά.
. Εξάλλου στη γεωμετρία ο στόχος είναι μέσα στο χαοτικό διάγραμμα να βρεις ποια είναι τα "connected" κατά κάποιον τρόπο μικρότερα σχήματα και να εστιάσεις σε αυτά.