 .
.2. Η μικρότερη γωνία ενός τριγώνου είναι το μισό της μεγαλύτερης του, τα μέτρα των πλευρών του είναι διαδοχικοί ακέραιοι.
Να βρεθούν τα μέτρα των πλευρών του.
3. Θεωρούμε το μέσον του ύψους που άγεται από την κορυφή
 κανονικού τετραέδρου, το οποίο ενώνουμε με τις υπόλοιπες κορυφές.
κανονικού τετραέδρου, το οποίο ενώνουμε με τις υπόλοιπες κορυφές. Να αποδειχθεί οτι το σχηματιζόμενο με αυτόν τον τρόπο τετράεδρο, έχει μια τρίεδρο στερεά γωνία τρισορθογώνια.
edit's
διόρθωση τίτλου (αντικατάσταση του ΠΜΔΜ από το Π.Μ.Δ.Μ.)
τσεκάρισμα των εκθετών στο 1ο από άλλη πηγή

 .Έστω ότι
.Έστω ότι  όπου
όπου  θετικός ακέραιος.
θετικός ακέραιος. .
. που είναι ισοδύναμο με
που είναι ισοδύναμο με  .
.  που δε γίνεται δεκτή γιατί η μικρότερη πλευρά του τριγώνου προκύπτει με αρνητικό μήκος ,
που δε γίνεται δεκτή γιατί η μικρότερη πλευρά του τριγώνου προκύπτει με αρνητικό μήκος ,  που δίνει τη λύση στο θέμα
που δίνει τη λύση στο θέμα .
.
 το κανονικό τετράεδρο και
το κανονικό τετράεδρο και  το μήκος της ακμής του,
το μήκος της ακμής του,  η προβολή του
η προβολή του  στη βάση
στη βάση  και
και  το μέσο του
το μέσο του  . Το σημείο
. Το σημείο  , όπου
, όπου  το μέσο της ακμής
το μέσο της ακμής  βρίσκουμε,
βρίσκουμε, 
 , βρίσκουμε
, βρίσκουμε  . Άρα
. Άρα  .
.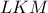 , έχουμε
, έχουμε  .
. (
( κάθετο στο επίπεδο της βάσης και
κάθετο στο επίπεδο της βάσης και  ).
). και
και  είναι ισοσκελή ορθογώνια και το ίδιο θα είναι και το τρίγωνο
είναι ισοσκελή ορθογώνια και το ίδιο θα είναι και το τρίγωνο  με
με  . Ομοίως βρίσκουμε ότι και
. Ομοίως βρίσκουμε ότι και  ,
,  .
.  είναι τρισορθογώνια, όπως αναζητούσαμε.
είναι τρισορθογώνια, όπως αναζητούσαμε. , το ύψος του
, το ύψος του  το μέσο του ύψους αυτού.
το μέσο του ύψους αυτού.  είναι ίσα, αν
είναι ίσα, αν  είναι το μέσον του
είναι το μέσον του 
 Όμοια έχουμε:
Όμοια έχουμε: 
 . Οπότε η αρχική παίρνει την μορφή:
. Οπότε η αρχική παίρνει την μορφή: 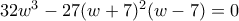 .
. . (1)
. (1) .
. .
. και
και  .
. και
και  .
.
 .
. και λύσεις
και λύσεις  .
. (διπλή ρίζα) και η
(διπλή ρίζα) και η  .
.