 είναι ρητός.
είναι ρητός.2. Δίνεται τρίγωνο
 με περίκεντρο
με περίκεντρο  και
και  τα μέσα των πλευρών
τα μέσα των πλευρών  αντίστοιχα.
αντίστοιχα. Θεωρούμε τα σημεία
 έτσι ώστε
έτσι ώστε  και
και  και με
και με  .
. Να αποδείξετε ότι οι ευθείες
 συντρέχουν.
συντρέχουν.3. Αν οι μη αρνητικοί πραγματικοί
 έχουν άθροισμα 2, να αποδείξετε ότι
έχουν άθροισμα 2, να αποδείξετε ότι  .
. Για ποιες τιμές των
 ισχύει η ισότητα;
ισχύει η ισότητα;4. Δίνονται οι διαφορετικοί μεταξύ τους μιγαδικοί
 των οποίων οι εικόνες
των οποίων οι εικόνες 
είναι διαδοχικά σημεία του κύκλου με κέντρο
 και ακτίνα
και ακτίνα 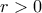 .
. Αν w είναι μια λύση της εξίσωσης
 και ισχύουν οι σχέσεις:
και ισχύουν οι σχέσεις: (Ι)
(Ι) (ΙΙ)
(ΙΙ)να αποδείξετε ότι:
α)το τρίγωνο
 είναι ισόπλευρο,
είναι ισόπλευρο,β)


 άρα:
άρα:
 θα είναι ο μεγαλύτερος εκ των
θα είναι ο μεγαλύτερος εκ των 

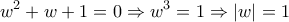
 και κυκλικά άρα
και κυκλικά άρα 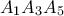 ισόπλευρο ομοίως το
ισόπλευρο ομοίως το 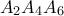
 ισόπλευρο και
ισόπλευρο και  σημείο του μικρού τόξου
σημείο του μικρού τόξου  του περιγεγραμμένου κύκλου τότε
του περιγεγραμμένου κύκλου τότε  που σημαίνει ότι
που σημαίνει ότι 
 χορδές με ίσες αντίστοιχες επίκεντρες γωνίες άρα
χορδές με ίσες αντίστοιχες επίκεντρες γωνίες άρα  και κυκλικά το ζητούμενο
και κυκλικά το ζητούμενο το ορθόκεντρο του
το ορθόκεντρο του  τέμνει την
τέμνει την  στο
στο  και κυκλικά για τις
και κυκλικά για τις 
 το οποίο είναι δύναμη του
το οποίο είναι δύναμη του  . Επομένως, για να είναι ο
. Επομένως, για να είναι ο  ρητός πρέπει να υπάρχουν φυσικοί
ρητός πρέπει να υπάρχουν φυσικοί  ώστε να συμβαίνει ένα από τα πιο κάτω
ώστε να συμβαίνει ένα από τα πιο κάτω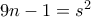 και
και 
 και
και  .
.  αλλά
αλλά  . Πρέπει λοιπόν
. Πρέπει λοιπόν  περιττός, έστω
περιττός, έστω  . Άρα
. Άρα 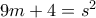 και
και  το οποίο δίνει
το οποίο δίνει  . Τότε
. Τότε 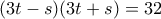 και επειδή
και επειδή 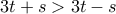 πρέπει να ισχύει ένα από τα πιο κάτω:
πρέπει να ισχύει ένα από τα πιο κάτω:

 .
. που δίνουν
που δίνουν  και το (γ) δίνει
και το (γ) δίνει  που δίνουν
που δίνουν  . Και στις δύο περιπτώσεις ο Α είναι ρητός. (
. Και στις δύο περιπτώσεις ο Α είναι ρητός. ( στην πρώτη περίπτωση και
στην πρώτη περίπτωση και  στην δεύτερη.)
στην δεύτερη.)