Καλησπέρα σε όλους!
Ολοκληρώθηκε χθες η 40ή Βαλκανική Μαθηματική Ολυμπιάδα στην Αττάλεια της Τουρκίας και σήμερα επιστρέφουμε στην Ελλάδα! Η εμφάνιση των μαθητών μας εξαιρετική, οι διακρίσεις τους πολλές (όλοι τους πήραν μετάλλιο), η γενική κατάταξη της χώρας υψηλή (4η ανάμεσα σε 23 χώρες που συμμετείχαν επίσημα ή ανεπίσημα στο διαγωνισμό) και υψηλότερη από παραδοσιακά δυνατές χώρες στα Μαθηματικά (Σερβία, Ηνωμένο Βασίλειο, Ιταλία, Γαλλία κλπ...).
Τα θέματα ιδιαίτερα απαιτητικά (το 4ο λύθηκε πλήρως μόνο από 1 παιδί ενώ περισσότερες από 1/10 μονάδες πήραν μόλις 8 από τους συνολικά 131 μαθητές που συμμετείχαν) αλλά οι μαθητές μας ανταποκρίθηκαν επάξια.
Αξίζει να σημειωθεί ότι το χρυσό μετάλλιο έπαιρνε όποιος μαθητής είχε βαθμολογία μεγαλύτερη του 31/40 (δηλαδή 3 πλήρως λυμένα θέματα και τουλάχιστον 2 μονάδες από το 4ο θέμα), το αργυρό για όποιο μαθητή είχε βαθμολογία 31/40 μονάδες (ναι! εκεί ΔΕΝ υπήρχε εύρος βαθμών. Μόνο όσοι πήραν 31 ακριβώς, πήραν αργυρό μετάλλιο) και το χάλκινο ήταν για όσους μαθητές πήραν βαθμολογία μεγαλύτερη του 16. Τρεις μαθητές μας πήραν αργυρό με βαθμολογία 31/40 (!!) χάνοντας το χρυσό για 1 μόλις πόντο, και 3 μαθητές μας πήραν χάλκινο με βαθμολογίες 30/40, 21/40, 20/40.
Αξίζει επίσης να σημειωθεί ότι το 3ο πρόβλημα του διαγωνισμού ήταν ελληνική πρόταση και το κατασκεύασαν από κοινού δύο παλαιότερα μέλη των αποστολών μας σε διαγωνισμούς: Ο Minos Margaritis και ο Jason Prodromidis. Έτσι, η Ελληνική Αποστολή στην Τουρκία είχε επιπλέον να διορθώσει τα γραπτά των δύο ομάδων της Τουρκίας (η διοργανώτρια χώρα συμμετέχει πάντοτε με δύο ομάδες μαθητών εκ των οποίων μόνο μία συμμετέχει επίσημα). Το πρόβλημα πολύ όμορφο αλλά αρκετά δύσκολο. Τέσσερα μέλη της αποστολής μας το έλυσαν πλήρως!
Έτσι, τα αποτελέσματα της

Ελληνικής Αποστολής

έχουν ως εξής:
Παναγιώτης Λιάμπας: Αργυρό Μετάλλιο 
Ορέστης Λιγνός: Αργυρό Μετάλλιο 
Γιώργος Τζαχρήστας: Αργυρό Μετάλλιο 
Πρόδρομος Φωτιάδης: Χάλκινο Μετάλλιο 
Κυριάκος Τσουρέκας: Χάλκινο Μετάλλιο 
Γιάννης Μαυρίκος: Χάλκινο Μετάλλιο 
Παιδιά για άλλη μία φορά ήταν τιμή μου που ήμουν μαζί σας σε αυτή τη διοργάνωση και σας εύχομαι από καρδιάς καλή πρόοδο σε ό,τι αποφασίσετε να κάνετε!
Τέλος, ευχαριστώ και τον Θάνο Μάγκο, υπαρχηγό της Ελληνικής Αποστολής με τον οποίο συνεργαστήκαμε καθ' όλη τη διάρκεια της ΒΜΟ, μοιραστήκαμε το άγχος και τις δυσκολίες κυρίως στη διαδικασία της διόρθωσης και υποστήριξης των γραπτών των μαθητών μας. Θα ήταν παράλειψή μου αν δεν ευχαριστούσα τον δικό μας Δημήτρη Χριστοφίδη, τον αρχηγό της Κύπρου για τη βοήθειά του στη διαδικασία της διόρθωσης των γραπτών της Ελλάδας αλλά και στη βοήθειά του κατά τη διάρκεια διόρθωσης των γραπτών της Τουρκίας.
 τέτοιες, ώστε για κάθε
τέτοιες, ώστε για κάθε  να ισχύει ότι
να ισχύει ότι .
. , του οποίου ο εγγεγραμμένος κύκλος εφάπτεται στις πλευρές
, του οποίου ο εγγεγραμμένος κύκλος εφάπτεται στις πλευρές  στα σημεία
στα σημεία 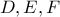 αντίστοιχα. Δίνεται επιπλέον ότι υπάρχει σημείο
αντίστοιχα. Δίνεται επιπλέον ότι υπάρχει σημείο  στην ευθεία
στην ευθεία  τέτοιο, ώστε
τέτοιο, ώστε  . Έστω
. Έστω  το μέσο του τόξου
το μέσο του τόξου  του περιγεγραμμένου κύκλου του τριγώνου
του περιγεγραμμένου κύκλου του τριγώνου  το οποίο δεν περιέχει το σημείο
το οποίο δεν περιέχει το σημείο  . Να αποδείξετε ότι η ευθεία
. Να αποδείξετε ότι η ευθεία 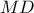 διέρχεται από το σημείο
διέρχεται από το σημείο  ή από το σημείο
ή από το σημείο  .
. , συμβολίζουμε με
, συμβολίζουμε με  το πλήθος των διακεκριμένων πρώτων διαιρετών του
το πλήθος των διακεκριμένων πρώτων διαιρετών του  (για παράδειγμα,
(για παράδειγμα,  και
και  ). Να προσδιορίσετε όλα τα πολυώνυμα
). Να προσδιορίσετε όλα τα πολυώνυμα  με ακέραιους συντελεστές τέτοια, ώστε όταν ο
με ακέραιους συντελεστές τέτοια, ώστε όταν ο  είναι θετικός ακέραιος με
είναι θετικός ακέραιος με  , τότε ο
, τότε ο  είναι επίσης θετικός ακέραιος με
είναι επίσης θετικός ακέραιος με  .
. για τον οποίο ισχύει το εξής: Οποτεδήποτε η Αλίκη χρωματίσει κόκκινους,
για τον οποίο ισχύει το εξής: Οποτεδήποτε η Αλίκη χρωματίσει κόκκινους,  ακριβώς αριθμούς από το σύνολο
ακριβώς αριθμούς από το σύνολο  , ο Βασίλης μπορεί να χρωματίσει μπλε, κάποιους από τους υπόλοιπους αχρωμάτιστους αριθμούς έτσι, ώστε το άθροισμα όλων των κόκκινων αριθμών να είναι ίσο με το άθροισμα όλων των μπλε αριθμών.
, ο Βασίλης μπορεί να χρωματίσει μπλε, κάποιους από τους υπόλοιπους αχρωμάτιστους αριθμούς έτσι, ώστε το άθροισμα όλων των κόκκινων αριθμών να είναι ίσο με το άθροισμα όλων των μπλε αριθμών.
 τέτοιες, ώστε για κάθε
τέτοιες, ώστε για κάθε  τη δοσμένη συνθήκη. Επίσης παρατηρώ ότι η μηδενική συνάρτηση είναι λύση οπότε θα υποθέσω ότι
τη δοσμένη συνθήκη. Επίσης παρατηρώ ότι η μηδενική συνάρτηση είναι λύση οπότε θα υποθέσω ότι 
 .
.
 είναι
είναι  .
. με
με  .
.


 .
. .
.
 ,
,  παίρνουμε
παίρνουμε 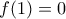 .
.


 .
. , τότε
, τότε 



 , τότε
, τότε 
 ,
,  , άτοπο.
, άτοπο. , οπότε στην πάνω είναι
, οπότε στην πάνω είναι  και ο ισχυρισμός ολοκληρώθηκε.
και ο ισχυρισμός ολοκληρώθηκε.
 οπότε για μη-μηδενικά
οπότε για μη-μηδενικά  :
: .
. ικανοποιεί τη ζητούμενη συνθήκη οπότε έχουμε ότι οι μη-μηδενικές λύσεις της εξίσωσης είναι οι:
ικανοποιεί τη ζητούμενη συνθήκη οπότε έχουμε ότι οι μη-μηδενικές λύσεις της εξίσωσης είναι οι: