Τεστ Εξάσκησης (54), Μικροί

#1

ΘΕΜΑ 1
Θεωρούμε τετράγωνο ABCD.

Έστω

σημείο του περιγεγραμμένου κύκλου του τετραγώνου ABCD

που βρίσκεται στο κυρτογώνιο τόξο

(διαφορετικό από τα

και

). Έστω

το σημείο τομής της

με τη διαγώνιο

και

το σημείο τομής της

με την

Να δείξετε ότι $MN \parallel BD.$

ΘΕΜΑ 2
Να βρεθούν όλες οι τριάδες (p,x,y)

τέτοιες ώστε p^x=y^4+4

, όπου

πρώτος και x,y

μη αρνητικοί ακέραιοι.

ΘΕΜΑ 3
Σε ένα τουρνουά σκάκι συμμετέχουν άνδρες και γυναίκες. Κάθε δύο συμμετέχοντες έπαιξαν μεταξύ τους ακριβώς μία φορά.
Σε περίπτωση νίκης, ο νικητής κερδίζει 1 βαθμό ενώ ο ηττημένος 0 βαθμούς. Σε περίπτωση ισοπαλίας, και οι δύο παίκτες παίρνουν από 0.5 βαθμό.
Παρατηρήθηκε ότι κάθε παίκτης (είτε άνδρας είτε γυναίκα) κέρδισε τον ίδιο αριθμό βαθμών στα παιχνίδια με τους άνδρες και στα παιχνίδια με τις γυναίκες. Να δείξετε ότι ο συνολικός αριθμός των συμμετεχόντων είναι τέλειο τετράγωνο ακεραίου.

ΘΕΜΑ 4
Να βρεθεί η ελάχιστη τιμή της σταθεράς

έτσι ώστε

$\displaystyle {a\left(\frac{x}{z}+\frac{y}{x}+\frac{z}{y}\right)\geq \frac{1}{x}+\frac{1}{y}+\frac{1}{z}+4(x+y+z)},$

για κάθε x,y,z>0

με

#2

socrates έγραψε: ↑
Δευ Μαρ 20, 2023 1:15 am
ΘΕΜΑ 1
Θεωρούμε τετράγωνο Έστω σημείο του περιγεγραμμένου κύκλου του τετραγώνου που βρίσκεται στο κυρτογώνιο τόξο (διαφορετικό από τα και ). Έστω το σημείο τομής της με τη διαγώνιο και το σημείο τομής της με την
Να δείξετε ότι $MN \parallel BD.$

: Μικροί(54).png (17.17 KiB) Προβλήθηκε 398 φορές

$\displaystyle C\widehat AB = D\widehat PC = 45^\circ,$ άρα το APNM

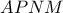είναι εγγράψιμο, οπότε $\displaystyle A\widehat MN = A\widehat PN = 90^\circ .$

Αλλά, $\displaystyle A\widehat OB = 90^\circ ,$ που σημαίνει ότι $\boxed{MN||BD}$

2nisic · #3

socrates έγραψε: ↑
Δευ Μαρ 20, 2023 1:15 am
ΘΕΜΑ 2
Να βρεθούν όλες οι τριάδες τέτοιες ώστε , όπου πρώτος και μη αρνητικοί ακέραιοι.

θα λύσουμε το εξής:
Να βρεθούν όλες οι τετράδες (p,x,y,z)

τέτοιες ώστε p^z=x^4+4y^4

, όπου

πρώτος και x,y,z

μη αρνητικοί ακέραιοι.
Έστω (x,y)=1

τότε:

οπότε τα

είναι δύναμης του

και επειδή
$(x-y)^2+y^2<(x+y)^2+y^2\Rightarrow (x-y)^2+y^2|(x+y)^2+y^2\Rightarrow (x-y)^2+y^2|4xy$
Όμως επειδή (x,y)=1

βρίσκουμε ότι ((x-y)^2+y^2,y)=1

και ότι

.
Οπότε $(x-y)^2+y^2|4xy\Rightarrow (x-y)^2+y^2|8\Rightarrow (x-y)^2+y^2=1,2,4,8$

Διακρίνοντας της περίπτωσης έχουμε της λύσης: (x,y,z,p)=(0,2^a,4a+2,2),(r^a,0,4a,r)(5^a,5^a,4a+1,5)

Τεστ Εξάσκησης (54), Μικροί

Τεστ Εξάσκησης (54), Μικροί

Re: Τεστ Εξάσκησης (54), Μικροί

Re: Τεστ Εξάσκησης (54), Μικροί

Μέλη σε σύνδεση