Παραθέτω τα θέματα του διαγωνισμού:
Πρόβλημα 1. Η τράπεζα του Όσλο εκδίδει δύο τύπους νομισμάτων: αλουμινίου (τύπου Α) και χαλκού (τύπου Β). Η Μαριάννα διαθέτει
 νομίσματα από αλουμίνιο και
νομίσματα από αλουμίνιο και  νομίσματα από χαλκό τοποθετημένα σε σειρά, σε μία τυχαία διάταξη. Μία αλυσίδα είναι μία υπακολουθία συνεχόμενων νομισμάτων του ίδιου τύπου. Δοθέντος ενός θετικού ακεραίου
νομίσματα από χαλκό τοποθετημένα σε σειρά, σε μία τυχαία διάταξη. Μία αλυσίδα είναι μία υπακολουθία συνεχόμενων νομισμάτων του ίδιου τύπου. Δοθέντος ενός θετικού ακεραίου  , η Μαριάννα εκτελεί επαναλαμβανόμενα την ακόλουθη πράξη: προσδιορίζει τη μεγαλύτερη αλυσίδα που περιέχει το
, η Μαριάννα εκτελεί επαναλαμβανόμενα την ακόλουθη πράξη: προσδιορίζει τη μεγαλύτερη αλυσίδα που περιέχει το  οστό νόμισμα από τα αριστερά και τοποθετεί όλα τα νομίσματα της αλυσίδας στα αριστερά της σειράς. Ένα παράδειγμα για
οστό νόμισμα από τα αριστερά και τοποθετεί όλα τα νομίσματα της αλυσίδας στα αριστερά της σειράς. Ένα παράδειγμα για  και
και 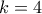 με την αρχική διάταξη
με την αρχική διάταξη  είναι το εξής:
είναι το εξής:
Να βρείτε όλα τα ζεύγη
 με
με  τέτοια ώστε για οποιαδήποτε αρχική διάταξη σε καποια στιγμή της διαδικασίας, τα πιο αριστερά
τέτοια ώστε για οποιαδήποτε αρχική διάταξη σε καποια στιγμή της διαδικασίας, τα πιο αριστερά  να είναι του ίδιου τύπου.
να είναι του ίδιου τύπου.Πρόβλημα 2. Έστω
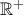 το σύνολο των θετικών πραγματικών αριθμών. Να βρείτε όλες τις συναρτήσεις
το σύνολο των θετικών πραγματικών αριθμών. Να βρείτε όλες τις συναρτήσεις  τέτοιες ώστε για κάθε
τέτοιες ώστε για κάθε  , υπάρχει ακριβώς ένας
, υπάρχει ακριβώς ένας  που ικανοποιεί την:
που ικανοποιεί την: 
Πρόβλημα 3. Έστω
 ένας θετικός ακέραιος και
ένας θετικός ακέραιος και  ένα πεπερασμένο σύνολο περιττών πρώτων αριθμών. Να δείξετε ότι υπάρχει το πολύ ένας τρόπος (με περιστροφές και συμμετρίες) να τοποθετηθούν τα στοιχεία του
ένα πεπερασμένο σύνολο περιττών πρώτων αριθμών. Να δείξετε ότι υπάρχει το πολύ ένας τρόπος (με περιστροφές και συμμετρίες) να τοποθετηθούν τα στοιχεία του  σε έναν κύκλο έτσι ώστε το γινόμενο οποιονδήποτε δύο γειτονικών να είναι της μορφής
σε έναν κύκλο έτσι ώστε το γινόμενο οποιονδήποτε δύο γειτονικών να είναι της μορφής  , για κάποιον θετικό ακέραιο
, για κάποιον θετικό ακέραιο  .
.Πρόβλημα 4. Έστω
 ένα κυρτό πεντάγωνο τέτοιο ώστε
ένα κυρτό πεντάγωνο τέτοιο ώστε  . Υποθέτουμε ότι υπάρχει ένα σημείο
. Υποθέτουμε ότι υπάρχει ένα σημείο  στο εσωτερικό του
στο εσωτερικό του  για το οποίο
για το οποίο  και
και  . Έστω ότι η ευθεία
. Έστω ότι η ευθεία  τέμνει τις
τέμνει τις  και
και  στα σημεία
στα σημεία  και
και  , αντίστοιχα. Υποθέτουμε ότι τα σημεία
, αντίστοιχα. Υποθέτουμε ότι τα σημεία  βρίσκονται πάνω στην ευθεία τους με αυτή τη σειρά. Έστω ότι η ευθεία
βρίσκονται πάνω στην ευθεία τους με αυτή τη σειρά. Έστω ότι η ευθεία  τέμνει τις
τέμνει τις  και
και 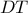 στα σημεία
στα σημεία  και
και  , αντίστοιχα. Υποθέτουμε ότι τα σημεία
, αντίστοιχα. Υποθέτουμε ότι τα σημεία  βρίσκονται πάνω στην ευθεία τους με αυτή τη σειρά. Να αποδείξετε ότι τα σημεία
βρίσκονται πάνω στην ευθεία τους με αυτή τη σειρά. Να αποδείξετε ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.Πρόβλημα 5. Να βρείτε όλες τις τριάδες
 θετικών ακεραίων με
θετικών ακεραίων με  πρώτο για τις οποίες:
πρώτο για τις οποίες:
Πρόβλημα 6. Έστω
 ένας θετικός ακέραιος. Ένα Σκανδιναβικό τετράγωνο είναι ένας πίνακας
ένας θετικός ακέραιος. Ένα Σκανδιναβικό τετράγωνο είναι ένας πίνακας  που περιέχει όλους τους θετικούς ακεραίους από το
που περιέχει όλους τους θετικούς ακεραίους από το  έως το
έως το  , έτσι ώστε κάθε κελί να περιέχει ακριβώς έναν αριθμό. Δύο διαφορετικά τετράγωνα θεωρούνται γειτονικά, αν έχουν μία κοινή πλευρά. Κάθε κελί που είναι γειτονικό μόνο με κελιά που περιέχουν μεγαλύτερους αριθμούς ονομάζεται κοιλάδα. Ένα ανηφορικό μονοπάτι είναι μία ακολουθία ενός ή περισσότερων κελιών έτσι ώστε:
, έτσι ώστε κάθε κελί να περιέχει ακριβώς έναν αριθμό. Δύο διαφορετικά τετράγωνα θεωρούνται γειτονικά, αν έχουν μία κοινή πλευρά. Κάθε κελί που είναι γειτονικό μόνο με κελιά που περιέχουν μεγαλύτερους αριθμούς ονομάζεται κοιλάδα. Ένα ανηφορικό μονοπάτι είναι μία ακολουθία ενός ή περισσότερων κελιών έτσι ώστε:(i) το πρώτο κελί στην ακολουθία να είναι κοιλάδα,
(ii) κάθε κελί της ακολουθίας είναι γειτονικό με το προηγούμενο κελί και
(iii) οι αριθμοί που είναι γραμμένοι στην ακολουθία βρίσκονται σε αύξουσα σειρά.
Να βρείτε, ως συνάρτηση του
 , τον ελάχιστο αριθμό ανηφορικών μονοπατιών σε ένα Σκανδιναβικό τετράγωνο.
, τον ελάχιστο αριθμό ανηφορικών μονοπατιών σε ένα Σκανδιναβικό τετράγωνο.Αρχηγός της αποστολής είναι ο κύριος Ανάργυρος Φελλούρης και υπαρχηγός ο Σιλουανός Μπραζιτίκος.


 , για κάθε
, για κάθε 
 για κάθε
για κάθε  (άμεσο π.χ. από AM-GM) και
(άμεσο π.χ. από AM-GM) και  (με ισότητα) για μία μοναδική τιμή, την
(με ισότητα) για μία μοναδική τιμή, την  .
.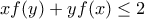 μπορεί ισοδύναμα να εκφραστεί ως εξής: υπάρχει μία καλά ορισμένη συνάρτηση
μπορεί ισοδύναμα να εκφραστεί ως εξής: υπάρχει μία καλά ορισμένη συνάρτηση  που δίνεται από τη σχέση
που δίνεται από τη σχέση  , το
, το  της παραπάνω.
της παραπάνω. 
 (δηλαδή, την
(δηλαδή, την  ) δίνει ότι υπάρχει μοναδικό
) δίνει ότι υπάρχει μοναδικό  τέτοιο ώστε
τέτοιο ώστε  , συνεπώς:
, συνεπώς:
 (λόγω της
(λόγω της  , άρα η συνάρτηση
, άρα η συνάρτηση  είναι involution (άρα και αμφιμονοσήμαντη/ bijective)
είναι involution (άρα και αμφιμονοσήμαντη/ bijective) ταυτοτικά (το οποίο ισχύει για τη λύση,
ταυτοτικά (το οποίο ισχύει για τη λύση, 
 είναι ολόκληρο το πεδίο ορισμού.
είναι ολόκληρο το πεδίο ορισμού. δεν είναι σταθερό σημείο, δηλαδή
δεν είναι σταθερό σημείο, δηλαδή  .
. (γίνεται καθώς
(γίνεται καθώς  , δηλαδή
, δηλαδή  .
. (ειδάλλως
(ειδάλλως 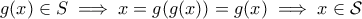 ) οπότε:
) οπότε:


 , π.χ. από την ανισότητα αριθμητικού-γεωμετρικού μέσου.
, π.χ. από την ανισότητα αριθμητικού-γεωμετρικού μέσου. για κάθε
για κάθε  .
.
 στη σχέση
στη σχέση  , λαμβάνουμε για κάθε
, λαμβάνουμε για κάθε 
 (είτε από αριστερά ή από δεξιά, το αποτέλεσμα είναι το ίδιο) σε αυτή την παράσταση λαμβάνουμε ότι:
(είτε από αριστερά ή από δεξιά, το αποτέλεσμα είναι το ίδιο) σε αυτή την παράσταση λαμβάνουμε ότι:
 , και συνδυάζοντας αυτό το αποτέλεσμα με την παραπάνω σχέση
, και συνδυάζοντας αυτό το αποτέλεσμα με την παραπάνω σχέση  όπως θέλαμε, η οποία ικανοποιεί.
όπως θέλαμε, η οποία ικανοποιεί. 
 άρτιος τότε πρέπει:
άρτιος τότε πρέπει: και
και 
 άρτιος και
άρτιος και 
 που δεν δίνει ακέραιες λύσεις.
που δεν δίνει ακέραιες λύσεις. οπότε η
οπότε η  παίρνει τις τιμές:
παίρνει τις τιμές: 
 από τις δυνατές περιπτώσεις, διότι για
από τις δυνατές περιπτώσεις, διότι για  το αποτέλεσμα λήγει σε
το αποτέλεσμα λήγει σε  δηλαδή δεν είναι τέλειο τετράγωνο. Επομένως, έχουμε την τριάδα
δηλαδή δεν είναι τέλειο τετράγωνο. Επομένως, έχουμε την τριάδα  .
. που απορρίπτεται.
που απορρίπτεται.
 τότε
τότε  που απορρίπτεται.
που απορρίπτεται. τότε
τότε  ομοίως δεν δίνει ακέραιες λύσεις.
ομοίως δεν δίνει ακέραιες λύσεις. τότε
τότε  που δίνει λύση για
που δίνει λύση για  . Οπότε, έχουμε την τριάδα
. Οπότε, έχουμε την τριάδα  .
.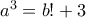 άρα το
άρα το  ή
ή  που δεν δίνει λύσεις.
που δεν δίνει λύσεις. άρα το
άρα το  που δεν δίνει λύσεις.
που δεν δίνει λύσεις. άρα το
άρα το  κανένα
κανένα  δεν το ικανοποιεί.
δεν το ικανοποιεί. ομοίως.
ομοίως.
 .
. τότε έχουμε
τότε έχουμε  και έτσι
και έτσι  , άτοπο. (προκύπτει εύκολα με επαγωγή)
, άτοπο. (προκύπτει εύκολα με επαγωγή) .
. .
. παίρνουμε
παίρνουμε  . Έστω
. Έστω  .
.
 .
.  τότε
τότε  , άτοπο για κάθε
, άτοπο για κάθε  και
και  . Τώρα
. Τώρα  .
. .
. τότε
τότε  , καθώς για μεγαλύτερο
, καθώς για μεγαλύτερο  . Άρα προκύπτει η λύση
. Άρα προκύπτει η λύση 
 τότε ελέγχουμε τις περιπτώσεις
τότε ελέγχουμε τις περιπτώσεις  που δίνουν την λύση
που δίνουν την λύση  .
.  παίρνουμε ότι
παίρνουμε ότι  ενώ
ενώ  , άτοπο.
, άτοπο. .
. τότε αν
τότε αν  έχουμε
έχουμε  , εύκολα άτοπο.
, εύκολα άτοπο. και
και 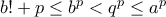 , άτοπο.
, άτοπο.  .
.![A=[i,j] A=[i,j]](/forum/ext/geomar/texintegr/latexrender/pictures/b01d81e4da55c0871337cb1e23a5aac3.png) η βασική αλυσίδα με το
η βασική αλυσίδα με το  -οστό και
-οστό και  -οστό νόμισμα να είναι το πρώτο και το τελευταίο αντίστοιχα.
-οστό νόμισμα να είναι το πρώτο και το τελευταίο αντίστοιχα.
 έχουμε ότι η διάταξη
έχουμε ότι η διάταξη  παραμένει ως είναι.
παραμένει ως είναι. παίρνουμε την διάταξη
παίρνουμε την διάταξη  , όπου κάθε βασική αλυσίδα αποτελείται από
, όπου κάθε βασική αλυσίδα αποτελείται από  νομίσματα αντίστοιχα. Επειδή ο αριθμός των νομισμάτων της τελευταίας αλυσίδας είναι
νομίσματα αντίστοιχα. Επειδή ο αριθμός των νομισμάτων της τελευταίας αλυσίδας είναι  έπεται ότι το
έπεται ότι το 
![k\in B=[l,m],l>1,m<2n, k\in B=[l,m],l>1,m<2n,](/forum/ext/geomar/texintegr/latexrender/pictures/a9d3e42e3675542549d7744c6f08d2ea.png) οι βασικές αλυσίδες
οι βασικές αλυσίδες ![B_1=[l{'},l-1],B_2=[m+1,m'] B_1=[l{'},l-1],B_2=[m+1,m']](/forum/ext/geomar/texintegr/latexrender/pictures/0f7e9791686a0a1262fa41b652458dbc.png) γίνονται μία και τελειώσαμε αφού είναι και αδύνατο να αυξηθούν.
γίνονται μία και τελειώσαμε αφού είναι και αδύνατο να αυξηθούν.![k\in C=[1,l] k\in C=[1,l]](/forum/ext/geomar/texintegr/latexrender/pictures/e7930b5f48a725863a5e6de46871be5d.png) είναι
είναι  που είναι το αποδεικτέο.
που είναι το αποδεικτέο.![k\in D=[m,2n] k\in D=[m,2n]](/forum/ext/geomar/texintegr/latexrender/pictures/4990199722896e2371530acee1181635.png) θα αποδείξουμε ότι οι βασικές αλυσίδες είναι πλήθους
θα αποδείξουμε ότι οι βασικές αλυσίδες είναι πλήθους  από αρχή της περιστεροφωλιάς έχουμε τουλάχιστον μία αλυσίδα με νομίσματα πλήθους
από αρχή της περιστεροφωλιάς έχουμε τουλάχιστον μία αλυσίδα με νομίσματα πλήθους  .
. 