Λάμπρος Κατσάπας έγραψε: ↑Πέμ Απρ 06, 2023 12:24 am
Δίνονται οι συναρτήσεις

και
 1. α)
1. α) Να αποδείξετε ότι η συνάρτηση
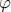
έχει μοναδική πραγματική ρίζα

.
β) Να δείξετε ότι ισχύει

και έπειτα ότι

.
2. Να μελετήσετε τη συνάρτηση

ως προς τη μονοτονία και τα ακρότατα.
3. Να αποδείξετε ότι
α) η συνάρτηση

είναι μια παράγουσα της

.
β)  4.
4. Αν για την παραγωγίσιμη και κυρτή στο

συνάρτηση

ισχύει

, για κάθε
![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png)
,
να αποδείξετε ότι
α) υπάρχει

τέτοιο, ώστε

και

.
β)  5.
5. Αν για τους πραγματικούς αριθμούς

ισχύει
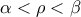
,
όπου

η ρίζα της συνάρτησης

, και
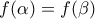
να αποδείξετε ότι

Καλημέρα

...ψάχνοντας τις δημοσιεύσεις βρήκα αυτή αναπάντητη ....και βγήκα μαζί της αλλά στο
5 ερώτημα τα χαλάσαμε λίγο...θα το κοιτάξω άλλη ώρα αν δεν δοθεί από κάποιον άλλον
ΛΥΣΗ
1.α) Είναι η συνάρτηση

και θεωρούμε την

που συνεχής ως πράξεις συνεχών με

και

οπότε ισχύει

και σύμφωνα με το θεώρημα του Bolzano

με

.
Τώρα η

είναι παραγωγίσιμη με

άρα είναι γνήσια φθίνουσα οπότε
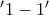
και τότε
η ρίζα μοναδική που είναι τότε μοναδική και της

αφού
 β)
β) Ισχύει

και επειδή

έχουμε

και επειδή

και
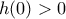
το
 2.
2. Είναι

παραγωγίσιμη με

και σύμφωνα με τα προηγούμενα για

άρα η

γνήσια φθίνουσα στο
![(-\infty ,\,\rho ] (-\infty ,\,\rho ]](/forum/ext/geomar/texintegr/latexrender/pictures/32982be580b71f454c4c83cf1c37604c.png)
και επίσης

άρα η

γνήσια αύξουσα στο

επομένως η

έχει ελάχιστο
το
 3. α
3. α) Είναι

παραγωγίσιμη με

οπότε είναι μία παράγουσα της
 β)
β) Είναι

άρα θέλουμε να δείξουμε ότι

ή ισοδύναμα

Τώρα αν

με

γίνεται

άρα θέλουμε να δείξουμε ότι

ή

που ισχύει γιατί
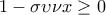
και όχι πάντα

και
επιπλέον αφού
![0\le \eta \mu x\le 1,\,\,x\in [0,\,\frac{\pi }{2}] 0\le \eta \mu x\le 1,\,\,x\in [0,\,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/3b2e907798c3d9898c3a77298fd24370.png)
είναι

και όχι πάντα μηδέν
αφού είναι

και για

και
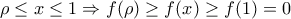 4. α)
4. α) Αν υπάρχει

πού

τότε από

θα έχουμε ότι

και επειδή

θα είναι

Αν τώρα

επειδή
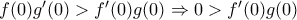
και

είναι

και επιπλέον

και

αναγκαία τότε

οπότε

και από θεώρημα Bolzano θα υπάρχει

τέτοιο, ώστε

άτοπο συμβαίνει όπως πριν
δηλαδή υπάρχει τελικά υπάρχει

τέτοιο, ώστε

και

.
β) Η εφαπτομένη στο

ή

της

είναι

και επειδή

κυρτή ισχύει ότι

και αφού

επειδή

λόγω της ανισότητας θα είναι

Φιλικά και Μαθηματικά
Βασίλης
 και
και 
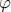 έχει μοναδική πραγματική ρίζα
έχει μοναδική πραγματική ρίζα  .
. και έπειτα ότι
και έπειτα ότι  .
. ως προς τη μονοτονία και τα ακρότατα.
ως προς τη μονοτονία και τα ακρότατα. είναι μια παράγουσα της
είναι μια παράγουσα της  .
.
 συνάρτηση
συνάρτηση  ισχύει
ισχύει  , για κάθε
, για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) ,
, τέτοιο, ώστε
τέτοιο, ώστε  και
και  .
.
 ισχύει
ισχύει 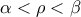 ,
,  η ρίζα της συνάρτησης
η ρίζα της συνάρτησης  , και
, και 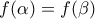


 και θεωρούμε την
και θεωρούμε την  που συνεχής ως πράξεις συνεχών με
που συνεχής ως πράξεις συνεχών με  και
και 
 και σύμφωνα με το θεώρημα του Bolzano
και σύμφωνα με το θεώρημα του Bolzano  με
με  .
. είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  άρα είναι γνήσια φθίνουσα οπότε
άρα είναι γνήσια φθίνουσα οπότε 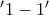 και τότε
και τότε  αφού
αφού 
 και επειδή
και επειδή  έχουμε
έχουμε  και
και 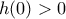 το
το  παραγωγίσιμη με
παραγωγίσιμη με  και σύμφωνα με τα προηγούμενα για
και σύμφωνα με τα προηγούμενα για  άρα η
άρα η ![(-\infty ,\,\rho ] (-\infty ,\,\rho ]](/forum/ext/geomar/texintegr/latexrender/pictures/32982be580b71f454c4c83cf1c37604c.png) και επίσης
και επίσης  άρα η
άρα η  επομένως η
επομένως η 
 οπότε είναι μία παράγουσα της
οπότε είναι μία παράγουσα της  άρα θέλουμε να δείξουμε ότι
άρα θέλουμε να δείξουμε ότι  ή ισοδύναμα
ή ισοδύναμα  με
με  γίνεται
γίνεται  άρα θέλουμε να δείξουμε ότι
άρα θέλουμε να δείξουμε ότι  ή
ή  που ισχύει γιατί
που ισχύει γιατί 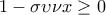 και όχι πάντα
και όχι πάντα  και
και ![0\le \eta \mu x\le 1,\,\,x\in [0,\,\frac{\pi }{2}] 0\le \eta \mu x\le 1,\,\,x\in [0,\,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/3b2e907798c3d9898c3a77298fd24370.png) είναι
είναι  και όχι πάντα μηδέν
και όχι πάντα μηδέν  και για
και για  και
και 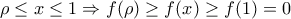
 πού
πού  τότε από
τότε από  και επειδή
και επειδή  θα είναι
θα είναι 
 επειδή
επειδή 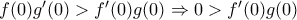 και
και  είναι
είναι  και επιπλέον
και επιπλέον  και
και αναγκαία τότε
αναγκαία τότε  οπότε
οπότε 
 άτοπο συμβαίνει όπως πριν
άτοπο συμβαίνει όπως πριν  ή
ή  της
της  και επειδή
και επειδή  και αφού
και αφού 


