
Οριακή κατάσταση
Συντονιστής: Μπάμπης Στεργίου
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1742
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Οριακή κατάσταση
Η προφανής λύση (για σύγκριση με άλλες , λιγότερο προφανείς )

και


και

Kαλαθάκης Γιώργης
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Οριακή κατάσταση
Υπάρχουν πολλοί τρόποι, αλλά ας δούμε έναν με ισοσυγκλίνουσες. Η απάντηση είναι
 , όπως φαίνεται από τα παρακάτω.
, όπως φαίνεται από τα παρακάτω. 
και αφού για
 ισχύει
ισχύει  (κάνε τις απλοποιήσεις για να το δεις), ισοδύναμα
(κάνε τις απλοποιήσεις για να το δεις), ισοδύναμα  , έχουμε
, έχουμε 
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Οριακή κατάσταση
Αξίζει να δούμε άλλον έναν τρόπο.
α) Εύκολα μπορούμε να δείξουμε (το κάνω παρακάτω) ότι
 και όμοια
και όμοια  .
.β) Με αυτά ως δεδομένα έχουμε
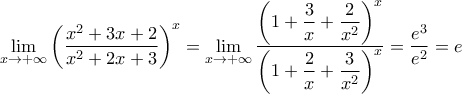 , όπως στις προηγούμενες λύσεις.
, όπως στις προηγούμενες λύσεις.Μένει να δούμε τους τύπους στο α). Βγαίνουν με πολλούς τρόπους Ένας είναι με λογάριθμους όπως ο τρόπος του Γιώργου παραπάνω. Άλλος είναι με ισοσυγκλίνουσες 'οπως στο προηγούμενο ποστ, ουσιαστικά ανάγοντάς τα στα
 και
και 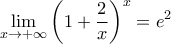
Τα αφήνω, για χάρη άλλου τρόπου, όπου γίνεται χρήση γνωστλων αποτελεσμάτων:
![\displaystyle{ \lim\limits_{x\to+\infty}\left(1+ \dfrac{3}{x} + \dfrac{2}{x^2}\right)^x= \lim\limits_{x\to+\infty}\left(1+ \dfrac{1}{ \dfrac {x^2}{3x+2}} \right)^x = \lim\limits_{x\to+\infty}\left [\left(1+ \dfrac{1}{ \dfrac {x^2}{3x+2}} \right)^{\dfrac {x^2}{3x+2} } \right ]^{\dfrac {3x+2}{x}} = } \displaystyle{ \lim\limits_{x\to+\infty}\left(1+ \dfrac{3}{x} + \dfrac{2}{x^2}\right)^x= \lim\limits_{x\to+\infty}\left(1+ \dfrac{1}{ \dfrac {x^2}{3x+2}} \right)^x = \lim\limits_{x\to+\infty}\left [\left(1+ \dfrac{1}{ \dfrac {x^2}{3x+2}} \right)^{\dfrac {x^2}{3x+2} } \right ]^{\dfrac {3x+2}{x}} = }](/forum/ext/geomar/texintegr/latexrender/pictures/842f72f493f07ce2528148ee65ffb943.png)
![\displaystyle{= \lim\limits_{x\to+\infty}\left [\left(1+ \dfrac{1}{ y} \right)^{y } \right ]^{\dfrac {3x+2}{x}} = e ^{3/1} = e^3 } \displaystyle{= \lim\limits_{x\to+\infty}\left [\left(1+ \dfrac{1}{ y} \right)^{y } \right ]^{\dfrac {3x+2}{x}} = e ^{3/1} = e^3 }](/forum/ext/geomar/texintegr/latexrender/pictures/e856b59ed3daca8eb9426779039b5f4f.png)
Όμοια το δεύτερο.
Ουσιαστικά η μέθοδος δείχνει ότι για oποιαδήποτε
 έχουμε
έχουμε 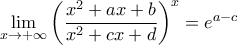
τελευταία επεξεργασία από Mihalis_Lambrou σε Κυρ Ιαν 15, 2023 9:53 am, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Οριακή κατάσταση
Η τελευταία λύση του Μιχάλη είναι περίπου αυτή την οποία είχα σκεφθεί ανεβάζοντας την άσκηση :


![\lim\limits_{x\to+\infty}\left[\left(1+\dfrac{1}{u}\right)^{u\right]^{\dfrac{x(x-1)}{x^2+2x+3}}}=e^1=e \lim\limits_{x\to+\infty}\left[\left(1+\dfrac{1}{u}\right)^{u\right]^{\dfrac{x(x-1)}{x^2+2x+3}}}=e^1=e](/forum/ext/geomar/texintegr/latexrender/pictures/555bc939dada630a895b1d21aa087224.png)


![\lim\limits_{x\to+\infty}\left[\left(1+\dfrac{1}{u}\right)^{u\right]^{\dfrac{x(x-1)}{x^2+2x+3}}}=e^1=e \lim\limits_{x\to+\infty}\left[\left(1+\dfrac{1}{u}\right)^{u\right]^{\dfrac{x(x-1)}{x^2+2x+3}}}=e^1=e](/forum/ext/geomar/texintegr/latexrender/pictures/555bc939dada630a895b1d21aa087224.png)
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Οριακή κατάσταση
Ας δούμε έναν τρόπο, νομίζω ότι είναι ο απλούστερος, στην περίπτωση που τα δύο τριώνυμα έχουν πραγματικές ρίζες. Εδώ δυστυχώς ο παρανομαστής έχει μιγαδικές. Γράφω όμως την μέθοδο στην περίπτωση που θέλουμε μία γκάμα ασκήσεων για να βάλουμε στους μαθητές μας.
Θέλουμε το
 όπου ο αριθμητής έχει ρίζες
όπου ο αριθμητής έχει ρίζες  και ο παρονομαστής
και ο παρονομαστής 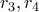 . Είναι τότε
. Είναι τότε 
 (Edit: διόρθωσα τυπογραφικά)
(Edit: διόρθωσα τυπογραφικά)(Σημειώνω ότι ισχύει και στην περίπτωση μιγαδικών ριζών διότι αληθεύει η
 , αλλά είναι εκτός σχολικής ύλης)
, αλλά είναι εκτός σχολικής ύλης)Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
