 για
για  .
.[Σίγουρα όχι τόσο δύσκολη (όσο η 'δυϊκή' της εδώ) ... αλλά χαριτωμένη!]
Συντονιστής: Μπάμπης Στεργίου
 για
για  .
.
 .
.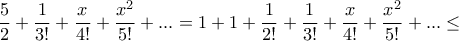
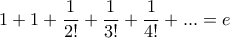 , απ' όπου προκύπτει η ζητούμενη ανισότητα.
, απ' όπου προκύπτει η ζητούμενη ανισότητα.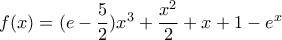 , και παρατηρούμε ότι
, και παρατηρούμε ότι  , αρκεί λοιπόν να αποδείξουμε ότι:
, αρκεί λοιπόν να αποδείξουμε ότι: είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 
 είναι θετική στο τυχόν τοπικό ακρότατο της στο
είναι θετική στο τυχόν τοπικό ακρότατο της στο 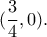
 προκύπτει από τις
προκύπτει από τις  και
και  για
για  : η τελευταία προκύπτει από τις
: η τελευταία προκύπτει από τις  ,
,  , και
, και  .
. προκύπτει από τις
προκύπτει από τις  ,
,  , και
, και  για
για  : για την τελευταία αρκεί, λόγω
: για την τελευταία αρκεί, λόγω  , η
, η 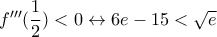 .
. προκύπτει από την
προκύπτει από την  , δηλαδή την
, δηλαδή την
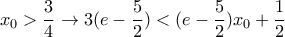 , άμεση από την
, άμεση από την  . [Όντως υπάρχει τέτοιο
. [Όντως υπάρχει τέτοιο  , με
, με  .]
.] : αυτό ίσως κάνει την απόδειξη μου MH σχολική, καθώς η όποια προσέγγιση του
: αυτό ίσως κάνει την απόδειξη μου MH σχολική, καθώς η όποια προσέγγιση του  απαιτεί γνώση της σχετικής σειράς, κλπ κλπ Δεδομένης και της όλης δυσκολίας της 'τριμερούς' απόδειξης μου, αλλά και της ύπαρξης της απλής αρχικής απόδειξης που παρέθεσε παραπάνω ο Κώστας, ανακύπτουν ερωτηματικά όσον αφορά το νόημα της παράθεσης της εδώ: δεν έχω ... τύψεις, μια και η σχετική μεθοδολογία θα μπορούσε κάλλιστα να είναι χρήσιμη σε κάποια άλλη σφικτή ανισότητα χωρίς απλή και 'εκ κατασκευής' απόδειξη**. (Επίσης ... η παράθεση της μπορεί να παρακινήσει άλλα μέλη να δώσουν άλλες αποδείξεις, που πολύ θα ήθελα να δω!)
απαιτεί γνώση της σχετικής σειράς, κλπ κλπ Δεδομένης και της όλης δυσκολίας της 'τριμερούς' απόδειξης μου, αλλά και της ύπαρξης της απλής αρχικής απόδειξης που παρέθεσε παραπάνω ο Κώστας, ανακύπτουν ερωτηματικά όσον αφορά το νόημα της παράθεσης της εδώ: δεν έχω ... τύψεις, μια και η σχετική μεθοδολογία θα μπορούσε κάλλιστα να είναι χρήσιμη σε κάποια άλλη σφικτή ανισότητα χωρίς απλή και 'εκ κατασκευής' απόδειξη**. (Επίσης ... η παράθεση της μπορεί να παρακινήσει άλλα μέλη να δώσουν άλλες αποδείξεις, που πολύ θα ήθελα να δω!)
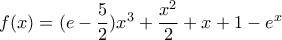 , οπότε
, οπότε  ,
,  ,
,  ,
, 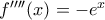 .
. δεν μπορεί να λαμβάνει και θετικές και αρνητικές τιμές στο
δεν μπορεί να λαμβάνει και θετικές και αρνητικές τιμές στο  , σε δύο σημεία
, σε δύο σημεία  και
και  ας πούμε (
ας πούμε ( ,
,  ): στην περίπτωση αυτή θα υπήρχε
): στην περίπτωση αυτή θα υπήρχε 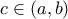 όπου
όπου  , άρα θα όφειλαν να υπάρχουν τουλάχιστον τρία σημεία μηδενισμού της
, άρα θα όφειλαν να υπάρχουν τουλάχιστον τρία σημεία μηδενισμού της  (ένα στο
(ένα στο  , ένα στο
, ένα στο  , και ένα στο
, και ένα στο  ), άρα και τουλάχιστον δύο σημεία μηδενισμού της
), άρα και τουλάχιστον δύο σημεία μηδενισμού της  στο
στο  ^ επειδή όμως η
^ επειδή όμως η  μηδενίζεται και στο
μηδενίζεται και στο  , θα πρέπει να υπάρχουν τουλάχιστον δύο σημεία μηδενισμού της
, θα πρέπει να υπάρχουν τουλάχιστον δύο σημεία μηδενισμού της  , άρα και ένα τουλάχιστον σημείο μηδενισμού της
, άρα και ένα τουλάχιστον σημείο μηδενισμού της  , άτοπο.
, άτοπο. όπου
όπου  . Δεν βλέπω κάποιον 'αφηρημένο', αλλά και σχολικότερο (!) τρόπο να προκύψει αυτό, μπορούμε όμως πάντα να λάβουμε
. Δεν βλέπω κάποιον 'αφηρημένο', αλλά και σχολικότερο (!) τρόπο να προκύψει αυτό, μπορούμε όμως πάντα να λάβουμε  , οπότε
, οπότε  (απαιτείται εδώ η γνώση της
(απαιτείται εδώ η γνώση της 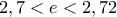 για την
για την  ).
).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες