Καλό βράδυ!
Κύριε Λάμπρου, σας ευχαριστώ για την εκτενή διαπραγμάτευση του θέματος. Η λύση σας είναι πιο μεθοδική από τη λύση που έκανα κατασκευάζοντας την άσκηση. Το λέω αυτό γιατί, όπως θα φανεί παρακάτω, ένα σημείο της λύσης είναι κάπως ουρανοκατέβατο. Επίσης, η λύση σας είναι χωρίς αμφιβολία εντός των σχολικών ορίων. Η λύση που θα καταγράψω χρησιμοποιεί το διωνυμικό θεώρημα ("το θεώρημα της στοιχειώδους άλγεβρας", που έγραψα στην εκφώνηση) και τους συνακόλουθους διωνυμικούς συντελεστές. Αν δεν κάνω λάθος, το διωνυμικό θεώρημα δε διδάσκεται απαραίτητα, αλλά νομίζω ότι υπάρχει σε κάποιο σχολικό βιβλίο του λυκείου. Τόλμησα, λοιπόν, να βάλω το θέμα σε φάκελο του λυκείου. Η γνώση του διωνυμικού θεωρήματος παραείναι στοιχειώδης για να μπει το θέμα σε πιο προχωρημένο φάκελο.
Έρχομαι στη λύση:
Χρησιμοποιώντας την υπόθεση δείχνουμε ότι:

, όπου

,
αφού μετά τις πράξεις γράφεται:

.
Αυτό το σημείο ήταν το ουρανοκατέβατο.
Με επαγωγή στο

τώρα, δείχνουμε ότι γενικά

, όπου

.
Από το διωνυμικό θεώρημα έχουμε ότι:
![1=[f(x)+(1-f(x)]^{2021}=(f(x))^{2021}+\binom{2021}{1}(f(x))^{2020}(1-f(x))+... 1=[f(x)+(1-f(x)]^{2021}=(f(x))^{2021}+\binom{2021}{1}(f(x))^{2020}(1-f(x))+...](/forum/ext/geomar/texintegr/latexrender/pictures/85dbeb3017f6a9424af04ca2671f5e0a.png)

.
Παίρνοντας ολοκλήρωμα από 0 έως 1 στην παραπάνω σχέση έχουμε ότι:


Αντικαθιστώντας τα γνωστά ολοκληρώματα από την υπόθεση έχουμε ότι:


.
Όμως, όπως δείξαμε (σχέση (1)), οι
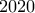
όροι του αθροίσματος του δεύτερου μέλους είναι ίσοι. Άρα, καθένας τους ισούται με

.
Στην περίπτωσή μας,

και τελικά:

.
Θα ήθελα να σχολιάσω ότι τέτοια συνάρτηση υπάρχει. Παράδειγμα είναι η ταυτοτική (

).Μάλιστα , μια πρόσφατη συζήτηση στο φόρουμ κινούνταν πέρι την αυτή θεματική (
https://www.mathematica.gr/forum/viewto ... 53&t=69941). Η μελέτη της εν λόγω συζήτησης ήταν και η αφορμή κατασκευής της άσκησης. Η επικαιρότητα του θέματος έχει , λοιπόν, δύο συνιστώσες. Μία είναι η παρουσία του αριθμού 2021 στα δεδομένα και η άλλη και πιο ουσιαστική είναι η εν λόγω πρόσφατη συζήτηση.
 . Για οποιουσδήποτε θετικούς ακεραίους
. Για οποιουσδήποτε θετικούς ακεραίους  ,
, .
. .
. .
.
 .
.

 ) μας δινόταν για φυσικούς
) μας δινόταν για φυσικούς  θα συνεχίζαμε την παραπάνω αλυσίδα ισοτήτων άλλη μία φορά. Τώρα το τελευταίο ολοκλήρωμα ισούται
θα συνεχίζαμε την παραπάνω αλυσίδα ισοτήτων άλλη μία φορά. Τώρα το τελευταίο ολοκλήρωμα ισούται  , του οποίου η τιμή μας δίνεται στις υποθέσεις ως
, του οποίου η τιμή μας δίνεται στις υποθέσεις ως  , και η άσκηση τέλειωσε. Να δούμε λοιπόν πώς θα παρακάμψουμε το πρόβλημα. Πίσω στο θέμα μας:
, και η άσκηση τέλειωσε. Να δούμε λοιπόν πώς θα παρακάμψουμε το πρόβλημα. Πίσω στο θέμα μας: ισχύει
ισχύει  . Υπόψη ότι για
. Υπόψη ότι για  αυτό δίνεται ως υπόθεση.
αυτό δίνεται ως υπόθεση.  δίνει
δίνει 
 . Δείξτε με ισχυρή επαγωγή ότι
. Δείξτε με ισχυρή επαγωγή ότι  για κάθε
για κάθε  . Υπόδειξη: Αρχίστε από τον αρχικό αναγωγικό τύπο αλλά με
. Υπόδειξη: Αρχίστε από τον αρχικό αναγωγικό τύπο αλλά με  .
. να συμπεράνετε ότι
να συμπεράνετε ότι 
 για κάθε
για κάθε  , και τελειώσαμε.
, και τελειώσαμε. 
 , όπου
, όπου  ,
, .
. τώρα, δείχνουμε ότι γενικά
τώρα, δείχνουμε ότι γενικά , όπου
, όπου  .
.![1=[f(x)+(1-f(x)]^{2021}=(f(x))^{2021}+\binom{2021}{1}(f(x))^{2020}(1-f(x))+... 1=[f(x)+(1-f(x)]^{2021}=(f(x))^{2021}+\binom{2021}{1}(f(x))^{2020}(1-f(x))+...](/forum/ext/geomar/texintegr/latexrender/pictures/85dbeb3017f6a9424af04ca2671f5e0a.png)
 .
.


 .
.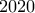 όροι του αθροίσματος του δεύτερου μέλους είναι ίσοι. Άρα, καθένας τους ισούται με
όροι του αθροίσματος του δεύτερου μέλους είναι ίσοι. Άρα, καθένας τους ισούται με  .
.
 .
. ).Μάλιστα , μια πρόσφατη συζήτηση στο φόρουμ κινούνταν πέρι την αυτή θεματική (
).Μάλιστα , μια πρόσφατη συζήτηση στο φόρουμ κινούνταν πέρι την αυτή θεματική ( . Tις δύο αυτές συναρτήσεις τις είχα εντοπίσει αλλά δεν μπορώ να βρω άλλη ούτε να αποδείξω ότι δεν υπάρχει άλλη. Όλα συνηγορούν ότι αυτές οι δύο είναι οι μόνες συναρτήσεις που ικανοποιούν τις συνθήκες. Για παράδειγμα οι υποψήφιες
. Tις δύο αυτές συναρτήσεις τις είχα εντοπίσει αλλά δεν μπορώ να βρω άλλη ούτε να αποδείξω ότι δεν υπάρχει άλλη. Όλα συνηγορούν ότι αυτές οι δύο είναι οι μόνες συναρτήσεις που ικανοποιούν τις συνθήκες. Για παράδειγμα οι υποψήφιες  μοιράζονται πολλές από τις ιδιότητές τους, όπως (έχω αποδείξει) τις εξής, πέρα από αυτές που ήδη έδειξα:
μοιράζονται πολλές από τις ιδιότητές τους, όπως (έχω αποδείξει) τις εξής, πέρα από αυτές που ήδη έδειξα:  (ακόμα και για
(ακόμα και για  ή
ή  )
) .
.  . Δεν κατάφερα να βρω εύκολο/άμεσο τρόπο, γι' αυτό και η μανούβρα στα βήματα 3) και 4) της λύσης μου. Αν είχαμε έναν εύκολο τρόπο να το δείξουμε, τότε η λύση απλοποιείται ουσιαστικά: Με εύκολη επαγωγή είναι τότε
. Δεν κατάφερα να βρω εύκολο/άμεσο τρόπο, γι' αυτό και η μανούβρα στα βήματα 3) και 4) της λύσης μου. Αν είχαμε έναν εύκολο τρόπο να το δείξουμε, τότε η λύση απλοποιείται ουσιαστικά: Με εύκολη επαγωγή είναι τότε  , και τα υπόλοιπα έπονται απλά.
, και τα υπόλοιπα έπονται απλά. ;
;