Να αποδειχθεί η ανισότητα
 για
για  .
.Συντονιστής: Μπάμπης Στεργίου
 για
για  .
. , στο
, στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) .
.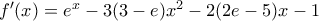



 .
. .
. και
και  τέτοια,
τέτοια, .
. τέτοιο, ώστε
τέτοιο, ώστε  .
. είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) οπότε μηδενίζεται μόνο στο
οπότε μηδενίζεται μόνο στο  και είναι αρνητική στο
και είναι αρνητική στο 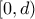 και θετική στο
και θετική στο ![(d,1] (d,1]](/forum/ext/geomar/texintegr/latexrender/pictures/b51a148cea3cfe85ea9b323031cbec81.png) .
. είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![[0,d] [0,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c16685098b1b281653b2cfe08bfaaa5b.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο ![[d,1] [d,1]](/forum/ext/geomar/texintegr/latexrender/pictures/f5dbfa5a8804773df765ab6203ce1ae4.png) και συνεπώς θα έχει το πολύ δύο ρίζες και εφόσον
και συνεπώς θα έχει το πολύ δύο ρίζες και εφόσον  , οι
, οι  και
και  είναι οι μοναδικές ρίζες της
είναι οι μοναδικές ρίζες της  .
. το οποίο μας δίνει τη μονοτονία της
το οποίο μας δίνει τη μονοτονία της  .
. είναι λοιπόν γνησίως αύξουσα στο
είναι λοιπόν γνησίως αύξουσα στο![[0,b] [0,b]](/forum/ext/geomar/texintegr/latexrender/pictures/e4c4135b88fbee27648b0a4ccbe9a875.png) , γνησίως φθίνουσα στο
, γνησίως φθίνουσα στο ![[b,c] [b,c]](/forum/ext/geomar/texintegr/latexrender/pictures/238bb374974bd3b5bf3b51c245fb1bdc.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο ![[c,1] [c,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3f2cdf4e28512200ff3bca64f51492f8.png) .
. ,
,  και
και  .
. πάει ως εξής :
πάει ως εξής : είναι θετική στο
είναι θετική στο  και αρνητική στο
και αρνητική στο  .
. είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![[0,a] [0,a]](/forum/ext/geomar/texintegr/latexrender/pictures/13596d6674a86fdafa24c4c414033e58.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![[a,1] [a,1]](/forum/ext/geomar/texintegr/latexrender/pictures/4b01978b77be38bfa26be75f89eb5322.png) .
. , η
, η 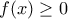 , για κάθε
, για κάθε ![x \in [0,1] x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) και η ισότητα πιάνεται μόνο στα άκρα.
και η ισότητα πιάνεται μόνο στα άκρα. , όπου
, όπου  , αρκεί επομένως να δειχθεί η
, αρκεί επομένως να δειχθεί η  για το τυχόν σημείο
για το τυχόν σημείο 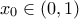 όπου
όπου  . Από την
. Από την  λαμβάνουμε
λαμβάνουμε  , οπότε με αντικατάσταση προκύπτει η
, οπότε με αντικατάσταση προκύπτει η![f(x_0)=x_0[-(3-e)x_0^2+(14-5e)x_0+(4e-11)]. f(x_0)=x_0[-(3-e)x_0^2+(14-5e)x_0+(4e-11)].](/forum/ext/geomar/texintegr/latexrender/pictures/462def1ff4ad35e33165816092a0ad21.png)
 θα προέκυπτε λοιπόν άμεσα από την
θα προέκυπτε λοιπόν άμεσα από την  για
για  , η οποία δυστυχώς δεν ισχύει (για πολύ μικρές τιμές του
, η οποία δυστυχώς δεν ισχύει (για πολύ μικρές τιμές του  ). Παρατηρούμε όμως ότι ισχύει για
). Παρατηρούμε όμως ότι ισχύει για  : πράγματι, θέτοντας
: πράγματι, θέτοντας  ισχύουν οι
ισχύουν οι  και
και  , οπότε η ζητούμενη είναι άμεση λόγω της κοιλότητας της
, οπότε η ζητούμενη είναι άμεση λόγω της κοιλότητας της  .
. για το τυχόν σημείο
για το τυχόν σημείο  όπου
όπου  . Αρκεί δηλαδή να δειχθεί η
. Αρκεί δηλαδή να δειχθεί η
 στο
στο ![[0, 1/2] [0, 1/2]](/forum/ext/geomar/texintegr/latexrender/pictures/a2e2bc3584b75b46bd95dea27174d767.png) προκύπτει από την κοιλότητα της στο διάστημα αυτό (άμεση συνέπεια της
προκύπτει από την κοιλότητα της στο διάστημα αυτό (άμεση συνέπεια της  ) και από τις
) και από τις  ,
,  .
. , το
, το  ]
] σε ένα έστω σημείο, όπως πχ εδώ), και, ακόμη περισσότερο, επειδή αποδεικνύει με τον ίδιο ακριβώς τρόπο την γενικότερη ανισότητα
σε ένα έστω σημείο, όπως πχ εδώ), και, ακόμη περισσότερο, επειδή αποδεικνύει με τον ίδιο ακριβώς τρόπο την γενικότερη ανισότητα για
για 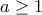 ,
,  .
. 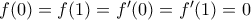 : είναι αξιοσημείωτο πως η επιπεδοποίηση στα άκρα οδηγεί σε τόσο καλές προσεγγίσεις εντός του διαστήματος -- εκθετική και τριτοβάθμια δεν ξεχωρίζουν καν στο γράφημα! -- και ακόμη πιο ενδιαφέρον ότι η σχετική σφιχτή ανισότητα προκύπτει τόσο εύκολα και ανώδυνα μέσω μιας απόδειξης όπως αυτή του Λάμπρου (#2)!
: είναι αξιοσημείωτο πως η επιπεδοποίηση στα άκρα οδηγεί σε τόσο καλές προσεγγίσεις εντός του διαστήματος -- εκθετική και τριτοβάθμια δεν ξεχωρίζουν καν στο γράφημα! -- και ακόμη πιο ενδιαφέρον ότι η σχετική σφιχτή ανισότητα προκύπτει τόσο εύκολα και ανώδυνα μέσω μιας απόδειξης όπως αυτή του Λάμπρου (#2)!Κάπως εναλλακτικά, και σύμφωνα με το παραπάνω παρενθετικό σχόλιο, αλλά και τα περί τρίτης παραγώγου που χρησιμοποίησε ο Λάμπρος, αρκεί να δείξουμε την θετικότητα της συνάρτησης-διαφοράς στοgbaloglou έγραψε: ↑Πέμ Ιούλ 29, 2021 8:00 pmΥπάρχει βεβαίως μια κάποια γοητεία στην 'ηρωική' μου απόδειξη (#3), πλην όμως ... πολύ πιο αποτελεσματική -- αλλά και πιο σχολική! -- είναι νομίζω η απόδειξη του Λάμπρου (#2), ειδικά επειδή καταφέρνει να αποδείξει το ζητούμενο χωρίς να 'λερώσουμε τα χέρια μας' (όπως ας πούμε να δείξουμε θετικότητα της συνάρτησης-διαφοράςσε ένα έστω σημείο, όπως πχ εδώ), και, ακόμη περισσότερο, επειδή αποδεικνύει με τον ίδιο ακριβώς τρόπο την γενικότερη ανισότητα
για
,
.
 , κάτι που ανάγεται στην ανισότητα
, κάτι που ανάγεται στην ανισότητα για
για 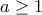 ,
,  .
. .)
.) Η προσέγγιση είναι πολύ καλή για σχετικά μικρές τιμές,Οι συντελεστές της τριτοβάθμιας προκύπτουν από την συνθήκη: είναι αξιοσημείωτο πως η επιπεδοποίηση στα άκρα οδηγεί σε τόσο καλές προσεγγίσεις εντός του διαστήματος -- εκθετική και τριτοβάθμια δεν ξεχωρίζουν καν στο γράφημα! -- και ακόμη πιο ενδιαφέρον ότι η σχετική σφιχτή ανισότητα προκύπτει τόσο εύκολα και ανώδυνα μέσω μιας απόδειξης όπως αυτή του Λάμπρου (#2)!
 ας πούμε. Το μέγιστο σφάλμα στο
ας πούμε. Το μέγιστο σφάλμα στο  -- η μέγιστη διαφορά εκθετικής και τριτοβάθμιας για
-- η μέγιστη διαφορά εκθετικής και τριτοβάθμιας για  -- δίνεται, ακολουθώντας την μέθοδο μου (#3) που βασίζεται στον υπολογισμό της
-- δίνεται, ακολουθώντας την μέθοδο μου (#3) που βασίζεται στον υπολογισμό της  με αντικατάσταση της
με αντικατάσταση της  από την
από την  , από τον τύπο
, από τον τύπο
![-(2(1+a)lna+(1+a)(lna)^2)x_0^2]. -(2(1+a)lna+(1+a)(lna)^2)x_0^2].](/forum/ext/geomar/texintegr/latexrender/pictures/cddb9c00230712d7c3371946653b2c33.png)
 , η πολύ ρεαλιστική προσέγγιση
, η πολύ ρεαλιστική προσέγγιση  δίνει μέγιστη διαφορά περίπου
δίνει μέγιστη διαφορά περίπου  ... κάτι που εξηγεί την ταύτιση των δύο γραφημάτων (εκθετικής και τριτοβάθμιας) που έχουμε ήδη αναφέρει.
... κάτι που εξηγεί την ταύτιση των δύο γραφημάτων (εκθετικής και τριτοβάθμιας) που έχουμε ήδη αναφέρει.Λάμπρο ΝΑΙ, νομίζω μάλιστα πως η απόδειξη σου (#2), σε αντίθεση με την δική μου (#5), δουλεύει για το παρακάτω γενικό:Λάμπρος Μπαλός έγραψε: ↑Σάβ Ιούλ 31, 2021 9:06 pmΠρώτα απ' όλα, θεωρώ εξαιρετική την άσκηση της δημοσίευσης. Αν "σπάσει" σε κατάλληλα ερωτήματα θα μπορούσε να αποτελέσει ένα ωραίο συμπαγές θέμα μελέτης συνάρτησης με ωραία πλοκή και κυρίως ένα ουσιώδες φινάλε. Έχει κάτι να δώσει και αυτό διότι κατασκευάστηκε πάνω στο τελείωμά της και όχι στην αρχή της με στυλ "πιάνω μια συνάρτηση, παραγωγίζω γιούργια κι όπου βγάλει στριμώχνω ερωτήματα".
Πέρα από αυτό, η μέθοδος (μπορεί να γίνει πιο στιβαρή ακόμη) επιδιώκει να προσεγγίσει μία συνάρτηση με ένα τριτοβάθμιο πολυώνυμο. Η συνάρτηση εδώ είναι η εκθετική. Λειτουργεί καλά σε όλες τις κυρτές (ή κοίλες) (Διορθώνω. Μάλλον σε αυτές με σταθερή μονοτονία τρίτης παραγώγου) σε κλειστά μικρά διαστήματα. Αυτό δεν είναι λίγο. Στις περιοχές κοντά στα άκρα η προσέγγιση είναι ισχυρότατη σε αντίθεση με το πολυώνυμο Taylor που έχει μεγάλη ισχύ γύρω από το μέσο (ας πούμε) του διαστήματος.
Το ερώτημα. Ποιά προσέγγιση είναι καλύτερη; Αυτή της δημοσίευσης ή το αντίστοιχο τριτοβάθμιο taylor στο μέσο; Αν έπρεπε να διαλέξουμε μία προσεγγιστική τριτοβάθμια πολυωνυμική συνάρτηση (όχι κλαδική) ποιά θα διαλέγαμε;
 ,
,  μηδενίζονται στα άκρα διαστήματος
μηδενίζονται στα άκρα διαστήματος ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) και η
και η  είναι γνησίως αύξουσα [φθίνουσα] στο
είναι γνησίως αύξουσα [φθίνουσα] στο  τότε η
τότε η  είναι θετική [αρνητική] στο
είναι θετική [αρνητική] στο  .
.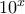 στο
στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) μαζί με τις δύο προσεγγίσεις της (Taylor και ... Μπαλόγλου-Μπαλού).
μαζί με τις δύο προσεγγίσεις της (Taylor και ... Μπαλόγλου-Μπαλού). στο
στο ![[0,k] [0,k]](/forum/ext/geomar/texintegr/latexrender/pictures/6c279203fd44ea566ecb1778414e009b.png) τότε λόγω του ότι
τότε λόγω του ότι  , θα δώσω το περιθώριο στο τριτοβάθμιο προσεγγιστικό να πάρει την κατηφόρα μετά το
, θα δώσω το περιθώριο στο τριτοβάθμιο προσεγγιστικό να πάρει την κατηφόρα μετά το  και δυστυχώς θα την πάρει. Η προσέγγιση χαλάει πολύ. Ενώ αν έκανα την ίδια προσέγγιση στο
και δυστυχώς θα την πάρει. Η προσέγγιση χαλάει πολύ. Ενώ αν έκανα την ίδια προσέγγιση στο ![[0.1, k] [0.1, k]](/forum/ext/geomar/texintegr/latexrender/pictures/73d8a44381d59baecdae7f8730b438e0.png) , ίσως να πήγαινε καλύτερα.
, ίσως να πήγαινε καλύτερα. , στο
, στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) (χαλαρό) ενώ
(χαλαρό) ενώ , στο
, στο ![[1,2] [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/f79408e5ca998cd53faf44af31e6eb45.png) (σφιχτό).
(σφιχτό). .
. είναι κυρτή. Μάλιστα , οι παράγωγοι όλων των τάξεων είναι θετικές, γεγονός που προκύπτει από την όσες φορές θέλουμε παραγώγιση της συνάρτησης στη μορφή της απειροσειράς (κάθε παράγωγος είναι γραμμικός συνδυασμός των
είναι κυρτή. Μάλιστα , οι παράγωγοι όλων των τάξεων είναι θετικές, γεγονός που προκύπτει από την όσες φορές θέλουμε παραγώγιση της συνάρτησης στη μορφή της απειροσειράς (κάθε παράγωγος είναι γραμμικός συνδυασμός των  με θετικούς συντελεστές).
με θετικούς συντελεστές).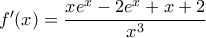 .
. και
και  .
. κυρτή , είναι πάνω από την εφαπτομένη στο
κυρτή , είναι πάνω από την εφαπτομένη στο  .
. , που είναι η ζητούμενη ανισότητα.
, που είναι η ζητούμενη ανισότητα. παρά στο
παρά στο  , κλπ).
, κλπ).

 (για
(για  πάντοτε).
πάντοτε). 
 .
. ![e^x-[(3-e)x^3+(2e-5)x^2+x+1]\leq 0,004371 e^x-[(3-e)x^3+(2e-5)x^2+x+1]\leq 0,004371](/forum/ext/geomar/texintegr/latexrender/pictures/2fa86a237c9230843bb4f2c879af7a7b.png) για
για 
![e^x-\left[\left(\dfrac{11-4e}{2}\right)x^4+(3e-8)x^3+\dfrac{x^2}{2}+x+1\right]\leq 0,000451 e^x-\left[\left(\dfrac{11-4e}{2}\right)x^4+(3e-8)x^3+\dfrac{x^2}{2}+x+1\right]\leq 0,000451](/forum/ext/geomar/texintegr/latexrender/pictures/8997d9a52b5a189b230ce2ffa559ae82.png) για
για  .
.![e^x-\left[\left(\dfrac{11-4e}{2}\right)x^4+(3e-8)x^3+\dfrac{x^2}{2}+x+1\right] e^x-\left[\left(\dfrac{11-4e}{2}\right)x^4+(3e-8)x^3+\dfrac{x^2}{2}+x+1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/5862406db44ebd8a2008331455d30c98.png) στο
στο  , αλλά κάτι τέτοιο δεν ισχύει. (Γενικότερα, πλήρη εποπτεία της διαμορφούμενης κατάστασης ΔΕΝ έχω...)]
, αλλά κάτι τέτοιο δεν ισχύει. (Γενικότερα, πλήρη εποπτεία της διαμορφούμενης κατάστασης ΔΕΝ έχω...)]Ας παρατηρηθεί ότι η παραπάνω τριτοβάθμια και τεταρτοβάθμια αποτελούν κάτω φράγμα της εκθετικής για όλο τοgbaloglou έγραψε: ↑Τρί Αύγ 10, 2021 8:51 pmΠολύ πολύ ενδιαφέρον, αγαπητέ Κώστα! Βρήκες έναν εντελώς διαφορετικό από τον δικό μου τρόπο παραγωγής του κάτω φράγματος, έναν τρόπο που σίγουρα με εκπλήσσει (αν και 'συμβατός' με την παρατήρηση του Λάμπρου για καλύτερη προσέγγιση στοπαρά στο
, κλπ).
Φυσικά η μέθοδος σου γενικεύεται για πολυώνυμα μεγαλύτερου βαθμού και καλύτερες προσεγγίσεις (όπως βέβαια και η αντίστοιχη για το άνω φράγμα εδώ), Χρησιμοποιώντας για παράδειγμα την

και την

... καταλήγουμε στο βελτιωμένο κάτω φράγμα
(για
πάντοτε).
Πράγματι, ισχύουν οι ανισότητες
Παρατηρούμε ότι η δεύτερη ανισότητα είναι ισοδύναμη προς την.
Όσον αφορά τις προσεγγίσεις, το WolframAlpha δίνει
για
και
για
.
[Ως εδώ οι βελτιώσεις: ήλπιζα πχ για μηδενισμό ΚΑΙ της δεύτερης παραγώγου τηςστο
, αλλά κάτι τέτοιο δεν ισχύει. (Γενικότερα, πλήρη εποπτεία της διαμορφούμενης κατάστασης ΔΕΝ έχω...)]
 και για το θετικό
και για το θετικό  , αντίστοιχα ... καθώς, στην μέθοδο του Κώστα, πολλαπλασιάζουμε τα δύο σκέλη της ανισότητας με
, αντίστοιχα ... καθώς, στην μέθοδο του Κώστα, πολλαπλασιάζουμε τα δύο σκέλη της ανισότητας με  και
και  , αντίστοιχα. Η μεταξύ τους ανισοτική σχέση, προκύπτουσα από την
, αντίστοιχα. Η μεταξύ τους ανισοτική σχέση, προκύπτουσα από την  , ισχύει βέβαια για όλο το
, ισχύει βέβαια για όλο το  . (Αντίστοιχες ανισοτικές σχέσεις για μεγαλύτερου βαθμού 'διαδοχικά' κάτω φράγματα προκύπτουν από την
. (Αντίστοιχες ανισοτικές σχέσεις για μεγαλύτερου βαθμού 'διαδοχικά' κάτω φράγματα προκύπτουν από την  .)
.)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες