 , βρείτε τα ακρότατα και τις ασύμπτωτες της
, βρείτε τα ακρότατα και τις ασύμπτωτες της  .
.Συντονιστής: Μπάμπης Στεργίου
 , βρείτε τα ακρότατα και τις ασύμπτωτες της
, βρείτε τα ακρότατα και τις ασύμπτωτες της  .
. και
και  . Η
. Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με 
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο 
 . Θεωρούμε τη συνάρτηση
. Θεωρούμε τη συνάρτηση  η οποία είναι παραγωγίσιμη στο
η οποία είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο  . Άρα
. Άρα
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![(1, e] (1, e]](/forum/ext/geomar/texintegr/latexrender/pictures/d94e4b6a6c2a012bbaacbd91255ece86.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο  . Από την άλλη όμως η
. Από την άλλη όμως η  είναι συνεχής στο
είναι συνεχής στο ![[4, 5] \subseteq (1, +\infty) [4, 5] \subseteq (1, +\infty)](/forum/ext/geomar/texintegr/latexrender/pictures/3c12e207afc827124ebf4bcbef50d936.png) . Είναι
. Είναι  και
και  συνεπώς υπάρχει μοναδικό ( λόγω μονοτονίας )
συνεπώς υπάρχει μοναδικό ( λόγω μονοτονίας )  τέτοιο ώστε
τέτοιο ώστε  . Επιπλέον επειδή η
. Επιπλέον επειδή η  παρουσιάζει ολικό ελάχιστο στο
παρουσιάζει ολικό ελάχιστο στο  έπεται ότι
έπεται ότι  για κάθε
για κάθε  και
και  για κάθε
για κάθε  . Έπεται λοιπόν ότι
. Έπεται λοιπόν ότι  για κάθε
για κάθε  και
και  για κάθε
για κάθε  . Συνεπώς η
. Συνεπώς η  παρουσιάζει ελάχιστο στο
παρουσιάζει ελάχιστο στο  . Υπολογίζουμε τώρα το όριο
. Υπολογίζουμε τώρα το όριο  .
.
![\displaystyle 1<2<x_0 \overset{g \;\; \begin{tikzpicture}
\draw [thick, >->] (0, 0.4) -- (0, 0);
\end{tikzpicture}}{\Leftarrow \! =\! \Rightarrow } g(2) > g(x_0) \Leftrightarrow 0 > g(x_0) \displaystyle 1<2<x_0 \overset{g \;\; \begin{tikzpicture}
\draw [thick, >->] (0, 0.4) -- (0, 0);
\end{tikzpicture}}{\Leftarrow \! =\! \Rightarrow } g(2) > g(x_0) \Leftrightarrow 0 > g(x_0)](/forum/ext/geomar/texintegr/latexrender/pictures/12b99047a5e10614861d38d62b785395.png)
 . Άρα
. Άρα 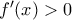 για κάθε
για κάθε  και
και  για κάθε
για κάθε  . Συνεπώς η
. Συνεπώς η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![(1, 2] (1, 2]](/forum/ext/geomar/texintegr/latexrender/pictures/97b7c0cb884b483e3107f779bdcadd64.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο  . Τέλος, η
. Τέλος, η  παρουσιάζει ολικό μέγιστο στο
παρουσιάζει ολικό μέγιστο στο 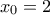 ίσο με
ίσο με  .
. 
 ) , ίσως δώσει μιαν ώθηση στο δεύτερο ζητούμενο .
) , ίσως δώσει μιαν ώθηση στο δεύτερο ζητούμενο .Εναλλακτικά για τηνTolaso J Kos έγραψε: ↑Κυρ Ιουν 13, 2021 1:01 pmΠρέπεικαι
. Η
είναι παραγωγίσιμη στο
με

Η συνάρτησηείναι παραγωγίσιμη στο
με παράγωγο

Παρατηρούμε επίσης ότι. Θεωρούμε τη συνάρτηση
η οποία είναι παραγωγίσιμη στο
με παράγωγο
. Άρα

Συνεπώς ηείναι γνησίως φθίνουσα στο
και γνησίως αύξουσα στο
. Από την άλλη όμως η
είναι συνεχής στο
. Είναι
και
συνεπώς υπάρχει μοναδικό ( λόγω μονοτονίας )
τέτοιο ώστε
. Επιπλέον επειδή η
παρουσιάζει ολικό ελάχιστο στο
έπεται ότι
για κάθε
και
για κάθε
. Έπεται λοιπόν ότι
για κάθε
και
για κάθε
. Συνεπώς η
παρουσιάζει ελάχιστο στο
. Υπολογίζουμε τώρα το όριο
.

Άρα
![\displaystyle 1<2<x_0 \overset{g \;\; \begin{tikzpicture}
\draw [thick, >->] (0, 0.4) -- (0, 0);
\end{tikzpicture}}{\Leftarrow \! =\! \Rightarrow } g(2) > g(x_0) \Leftrightarrow 0 > g(x_0) \displaystyle 1<2<x_0 \overset{g \;\; \begin{tikzpicture}
\draw [thick, >->] (0, 0.4) -- (0, 0);
\end{tikzpicture}}{\Leftarrow \! =\! \Rightarrow } g(2) > g(x_0) \Leftrightarrow 0 > g(x_0)](/forum/ext/geomar/texintegr/latexrender/pictures/12b99047a5e10614861d38d62b785395.png)
Οπότε. Άρα
για κάθε
και
για κάθε
. Συνεπώς η
είναι γνησίως αύξουσα στο
και γνησίως φθίνουσα στο
. Τέλος, η
παρουσιάζει ολικό μέγιστο στο
ίσο με
.
 : για
: για  εύκολα
εύκολα  λόγω
λόγω  και
και  , άμεση από τις
, άμεση από τις  και
και  , για την
, για την  για
για 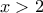 αρκεί, λόγω των
αρκεί, λόγω των  και
και  (αποδείχτηκε παραπάνω), να δειχθεί η
(αποδείχτηκε παραπάνω), να δειχθεί η  για το τυχόν σημείο
για το τυχόν σημείο  όπου
όπου  , αρκεί δηλαδή να δειχθεί η
, αρκεί δηλαδή να δειχθεί η  για
για  (αρκετά εύκολη και ανεξαρτήτου ενδιαφέροντος).
(αρκετά εύκολη και ανεξαρτήτου ενδιαφέροντος).Θανάση , είναι η πρώτη φορά στα
 χρόνια που γράφω τέτοια μακροστελέστατη απόδειξη για μονοτονία συνάρτησης. Δε λέω , στρωτές παραγώγους έχει , αλλά πρώτη φορά βλέπω απόδειξη μονοτονίας που απαιτεί σύνολο τιμών , Bolzano , και άλλα πράγματα. Κατά τα άλλα , καλή ήταν τη χάρηκα την άσκηση.
χρόνια που γράφω τέτοια μακροστελέστατη απόδειξη για μονοτονία συνάρτησης. Δε λέω , στρωτές παραγώγους έχει , αλλά πρώτη φορά βλέπω απόδειξη μονοτονίας που απαιτεί σύνολο τιμών , Bolzano , και άλλα πράγματα. Κατά τα άλλα , καλή ήταν τη χάρηκα την άσκηση.Αυτές είναι το εύκολο κομμάτι. Πράγματι, όπως βλέπουμε και από το σχήμα στο
 η
η 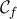 δε παρουσιάζει ασύμπτωτη αφού
δε παρουσιάζει ασύμπτωτη αφού  . Θα δούμε ότι στο
. Θα δούμε ότι στο  έχουμε οριζόντια ασύμπτωτη την
έχουμε οριζόντια ασύμπτωτη την  . Αυτό όμως είναι άμεσο αφού
. Αυτό όμως είναι άμεσο αφού

Τώρα που πέρασε η λαίλαπα των Πανελλαδικών: τα παραπάνω αποτελούν αυτοδύναμη απόδειξη της δοθείσης (όπου βέβαια
 είναι, όπως και στην απόδειξη του Τόλη, ο αριθμητής της παραγώγου της
είναι, όπως και στην απόδειξη του Τόλη, ο αριθμητής της παραγώγου της  )^ επισυνάπτω και ένα γράφημα των τριών σχετικών συναρτήσεων, όπου βλέπουμε πως
)^ επισυνάπτω και ένα γράφημα των τριών σχετικών συναρτήσεων, όπου βλέπουμε πως  (σημείο μηδενισμού της πράσινης συνάρτησης ΚΑΙ σημείο τομής της μπλε και της κόκκινης συνάρτησης). [Στην μέθοδο αυτή (που δεν ξέρω πόσο δημοφιλής είναι) ... απαιτείται η αρνητικότητα της κόκκινης συνάρτησης σε ολόκληρο το διάστημα όπου μπορεί να κινείται το
(σημείο μηδενισμού της πράσινης συνάρτησης ΚΑΙ σημείο τομής της μπλε και της κόκκινης συνάρτησης). [Στην μέθοδο αυτή (που δεν ξέρω πόσο δημοφιλής είναι) ... απαιτείται η αρνητικότητα της κόκκινης συνάρτησης σε ολόκληρο το διάστημα όπου μπορεί να κινείται το  (στο
(στο  δηλαδή), και όχι απλώς για
δηλαδή), και όχι απλώς για  : στο συγκεκριμένο πρόβλημα αυτό συμβαίνει και αποδεικνύεται εύκολα, σε αρκετά άλλα προβλήματα ΟΧΙ.]
: στο συγκεκριμένο πρόβλημα αυτό συμβαίνει και αποδεικνύεται εύκολα, σε αρκετά άλλα προβλήματα ΟΧΙ.]Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες