 είναι πλάγια ασύμπτωτος της
είναι πλάγια ασύμπτωτος της 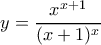 .
.[Οριακά σχολική η λύση μου, αλλά για θέμα Πανελλαδικών ΔΕΝ ΝΟΜΙΖΩ -- ας μην ανησυχούν όσοι υποψήφιοι δεν μπορούν να το λύσουν
Συντονιστής: Μπάμπης Στεργίου
 είναι πλάγια ασύμπτωτος της
είναι πλάγια ασύμπτωτος της 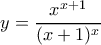 .
.Καλησπέρα
 είναι πλάγια ασύμπτωτη της
είναι πλάγια ασύμπτωτη της  στο
στο  αρκεί να αποδείξουμε ότι:
αρκεί να αποδείξουμε ότι: , και
, και .
. .
. , τότε είναι
, τότε είναι  , οπότε μπορούμε να θέσουμε
, οπότε μπορούμε να θέσουμε  , με
, με  , καθώς
, καθώς  , και
, και  , οπότε
, οπότε 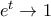 και
και  , συνεπώς
, συνεπώς  .
. , προκύπτει
, προκύπτει 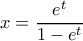 . Συνεπώς,
. Συνεπώς,  .
.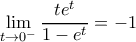 , καθώς τότε θα είναι
, καθώς τότε θα είναι .
. , συνεπώς είναι:
, συνεπώς είναι: 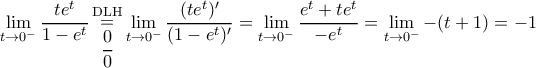 , οπότε η απόδειξη ολοκληρώθηκε.
, οπότε η απόδειξη ολοκληρώθηκε. .
. με
με  . Τότε, είναι:
. Τότε, είναι: .
.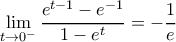 , και
, και
 , συνεπώς είναι:
, συνεπώς είναι:
 , συνεπώς προκύπτει ότι:
, συνεπώς προκύπτει ότι: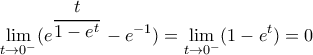 , συνεπώς είναι:
, συνεπώς είναι: .
. .
. . Συνεπώς, αρκεί να δείξουμε ότι
. Συνεπώς, αρκεί να δείξουμε ότι  .
. , συνεπώς είναι:
, συνεπώς είναι:

![\lim_{x\rightarrow +\infty}\left(2x+1\right)\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]=0 \lim_{x\rightarrow +\infty}\left(2x+1\right)\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]=0](/forum/ext/geomar/texintegr/latexrender/pictures/2836c9c02fa81ba4551143f2c2aadcbf.png)
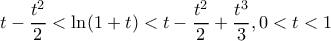




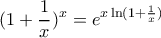







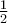


Δεξιοτεχνικές οι αποδείξεις του Ορέστη και του Σταύρου, και αντιποδικές όσον αφορά την χρήση ή μη DLH, ας παραθέσω και εγώ την 'ενδιάμεση' δική μου, ξεκινώντας από το παραπάνω λήμμα ... που πηγάζει από την

 )
)![0<\left(2x+1\right)\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]<\dfrac{2}{x}. 0<\left(2x+1\right)\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]<\dfrac{2}{x}.](/forum/ext/geomar/texintegr/latexrender/pictures/73fa617572bc10aa02d2bd53ea5fbf9b.png)
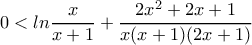 , που προκύπτει από τις
, που προκύπτει από τις (λόγω
(λόγω  ) και
) και .
. , που προκύπτει από τις
, που προκύπτει από τις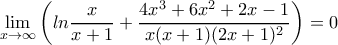 (λόγω
(λόγω  ) και
) και
![\displaystyle\lim_{x\rightarrow \infty}x\cdot \left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]=0. \displaystyle\lim_{x\rightarrow \infty}x\cdot \left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]=0.](/forum/ext/geomar/texintegr/latexrender/pictures/6a70249b28aa79c8146989b9d86a478e.png)
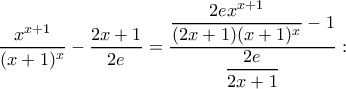

![\displaystyle\lim_{x\rightarrow +\infty}\left[\dfrac{x^{x+1}}{(x+1)^x}-\dfrac{2x+1}{2e}\right]=}\lim_{x\rightarrow +\infty} \dfrac{-x^{x+1}}{2(x+1)^x}\cdot \left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]=0, \displaystyle\lim_{x\rightarrow +\infty}\left[\dfrac{x^{x+1}}{(x+1)^x}-\dfrac{2x+1}{2e}\right]=}\lim_{x\rightarrow +\infty} \dfrac{-x^{x+1}}{2(x+1)^x}\cdot \left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]=0,](/forum/ext/geomar/texintegr/latexrender/pictures/c4162c84a85ee90fdd5820d49c5678ad.png)
 )
)![0<\dfrac{x^{x+1}}{(x+1)^x}\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]<x\cdot\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]. 0<\dfrac{x^{x+1}}{(x+1)^x}\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right]<x\cdot\left[(2x+1)\left(\dfrac{1}{x}+\dfrac{1}{x+1}+ln\dfrac{x}{x+1}\right)-2\right].](/forum/ext/geomar/texintegr/latexrender/pictures/406bea2d0a96b44afa070fc841722573.png)


 απο DLH
απο DLH
 αφού
αφού 



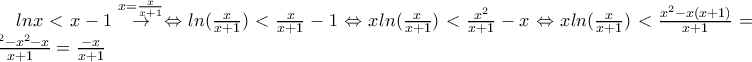




Αγαπητέ Νίκο, και στα Μαθηματικά και στην ζωή γενικότερα, καλό είναι να θέτουμε στόχους, να γνωρίζουμε που βρισκόμαστε και που θέλουμε να πάμε, κλπ Στην παρούσα περίπτωση, ουσιαστικά ήδη γνωρίζουμε το όριο που υπολόγισες (με το κριτήριο της παρεμβολής) λόγω της
 και του ορισμού του
και του ορισμού του  .
. ως ενδιαφέρουσα ασκησούλα, άσχετη όμως ουσιαστικά με το πρόβλημα που έθεσα.
ως ενδιαφέρουσα ασκησούλα, άσχετη όμως ουσιαστικά με το πρόβλημα που έθεσα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες