 είναι σημείο της διαμέτρου
είναι σημείο της διαμέτρου  ενός ημικυκλίου ώστε :
ενός ημικυκλίου ώστε :  . Από το
. Από το  αναχωρεί
αναχωρείφωτεινή ακτίνα η οποία ανακλάται στον "θόλο" του ημικυκλίου , σε σημείο του ,
 και συνεχίζοντας
και συνεχίζονταςξανασυναντά την διάμετρο στο
 .
.α) Δημιουργήστε συνάρτηση , η οποία να αποδίδει το μήκος της διαδρομής του φωτός .
β) Δείξτε ότι όταν η διαδρομή αυτή ελαχιστοποιηθεί , θα είναι :
 .
.
 είναι διχοτόμος.
είναι διχοτόμος. το μέσο του
το μέσο του  τότε έχουμε
τότε έχουμε
 .
. είναι διχοτόμος του τριγώνου
είναι διχοτόμος του τριγώνου  Έστω
Έστω  με
με  οπότε:
οπότε:


 είναι
είναι  άρα το ζητούμενο άθροισμα ελαχιστοποιείται
άρα το ζητούμενο άθροισμα ελαχιστοποιείται 
 Είναι όμως,
Είναι όμως, 


 kαι αν
kαι αν  \widehat{SOT}}
\widehat{SOT}} έχουμε
έχουμε oπότε
oπότε
 είναι
είναι 

 προς την διχοτόμο
προς την διχοτόμο  τέμνουν τις
τέμνουν τις  στα
στα 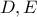 αντίστοιχα
αντίστοιχα  ισοσκελές τραπέζιο
ισοσκελές τραπέζιο και
και 
