ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Μαρ 26, 2020 11:27 pm
Θεωρούμε την συνεχή συνάρτηση

για την οποία ισχύει

a)Να δείξετε ότι υπάρχει σημείο της

που απέχει ελάχιστη απόσταση από το

b)Αν επιπλέον η

είναι παραγωγίσημη και

είναι ένα από τα σημεία της

που απέχει ελάχιστη απόσταση από το

να δείξετε ότι το

είναι κάθετο στην εφαπτομένη της

στο

(

)
Οι αρχικές μου σκέψεις και για το (β) ερώτημα ήταν κάπως γεωμετρικές, δεν είμαι σίγουρως αν είναι αυστηρές και σωστές και δεν τις έγραψα. Αφού όμως συνέχισε η κουβέντα, ας τις γράψω.

- elaxisth_apostash_grafhmatos.png (9.8 KiB) Προβλήθηκε 1711 φορές
β) Θεωρώ την συνάρτηση

στο διάστημα

, όπου

η ελάχιστη απόσταση της συνάρτησης

από την αρχή των αξόνων και

η συνάρτηση του ημικύκλιο ακτίνας

με κέντρο την αρχή των αξόνων.
Στο παραπάνω διάστημα είναι

γιατί διαφορετικά θα υπήρχε σημείο
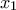
για το οποίο

. Δηλαδή το σημείο

θα ήταν εσωτερικό του κύκλου και η απόσταση από το

θα ήταν μικρότερη του

.
Η συνάρτηση

είναι παραγωγίσιμη ως άθροισμα παραγωγίσιμων συναρτήσεων. Και επειδή τα σημεία ελαχίστου απόστασης

είναι και σημεία στα οποία η

λαμβάνει την ελάχιστη τιμή της

, από το θεώρημα του Fermat θα είναι

. Η εφαπτομένη όμως της

σε ένα σημείο της (ημικυκλίου) είναι κάθετη στην ακτίνα που συνδέει αυτό το σημείο. Άρα και η εφαπτομένη της

στη θέση ελαχίστου θα είναι κάθετη σε αυτό το ελάχιστο ευθύγραμμο τμήμα.
Ομοίως εργαζόμαστε στην περίπτωση που τα σημεία ελαχίστου απόστασης βρίσκονται στο άλλο ημικύκλιο.
Αν δεν κάνω λάθος μπορεί να δειχθεί ότι αν η συνάρτηση

δέχεται κάθετη εφαπτομένη σε ένα σημείο τότε αυτό δεν μπορεί να είναι σημείο ελάχιστης απόστασης.




 είναι παραγωγίσημη και
είναι παραγωγίσημη και 
 που απέχει ελάχιστη απόσταση από το
που απέχει ελάχιστη απόσταση από το 
 είναι κάθετο στην εφαπτομένη της
είναι κάθετο στην εφαπτομένη της  στο
στο 
 )
)
 του γραφήματος από το
του γραφήματος από το  . Ως συνεχής και θετική συνάρτηση, έχει ολικό ελάχιστο.
. Ως συνεχής και θετική συνάρτηση, έχει ολικό ελάχιστο. . Άρα από τον μηδενισμό του αριθμητή έχουμε
. Άρα από τον μηδενισμό του αριθμητή έχουμε  . Δεδομένου ότι η κλίση της εφαπτομένης είναι
. Δεδομένου ότι η κλίση της εφαπτομένης είναι  και της
και της  , έπεται η ζητούμενη καθετότητα.
, έπεται η ζητούμενη καθετότητα. στο διάστημα
στο διάστημα ![[-|f(0)|, |f(0)|] [-|f(0)|, |f(0)|]](/forum/ext/geomar/texintegr/latexrender/pictures/f687178cbc236002b7996a8ce7279eb2.png) , που είναι συνεχής. Άρα υπάρχει σημείο στο οποίο λαμβάνει την ελάχιστη τιμή της σε αυτό το διάστημα. Έστω
, που είναι συνεχής. Άρα υπάρχει σημείο στο οποίο λαμβάνει την ελάχιστη τιμή της σε αυτό το διάστημα. Έστω  , με
, με  . Θα δείξουμε ότι για τα σημεία εκτός του παραπάνω διαστήματος η απόσταση δεν μπορεί να είναι μικρότερη από αυτή την ελάχιστη.
. Θα δείξουμε ότι για τα σημεία εκτός του παραπάνω διαστήματος η απόσταση δεν μπορεί να είναι μικρότερη από αυτή την ελάχιστη.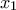 , με
, με  σημείο για το οποίο η απόσταση
σημείο για το οποίο η απόσταση  του σημείου
του σημείου  από το σημείο
από το σημείο  είναι ίση με
είναι ίση με 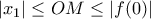 . Άτοπο.
. Άτοπο. ελαχίστου έχουμε
ελαχίστου έχουμε  , όπως θέλαμε.
, όπως θέλαμε. είναι κάθετη στην εφαπτομένη , διότι αν δεν ήταν , θα ήταν κάποια άλλη , ας πούμε η
είναι κάθετη στην εφαπτομένη , διότι αν δεν ήταν , θα ήταν κάποια άλλη , ας πούμε η  .
. ,άτοπο .
,άτοπο . τέμνει την εφαπτομένη, δεν είναι κατ' ανάγκη σημείο της καμπύλης. Οπότε ισχύει με
τέμνει την εφαπτομένη, δεν είναι κατ' ανάγκη σημείο της καμπύλης. Οπότε ισχύει με  αλλά δεν δίνει άτοπο.
αλλά δεν δίνει άτοπο.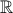 , οπότε για να επικαλεστούμε το σχολικό βιβλίο πρέπει ακόμα να πούμε ότι αφού
, οπότε για να επικαλεστούμε το σχολικό βιβλίο πρέπει ακόμα να πούμε ότι αφού  μπορούμε χωρίς βλάβη να περιοριστούμε σε διάστημα tτης μορφής
μπορούμε χωρίς βλάβη να περιοριστούμε σε διάστημα tτης μορφής ![[-M,M] [-M,M]](/forum/ext/geomar/texintegr/latexrender/pictures/f9b7329df8a2ac4dd6453f4a08ed77a5.png) όπου έξω από αυτό η συνάρτηση παίρνει μεγάλες τιμές (μας αρκεί
όπου έξω από αυτό η συνάρτηση παίρνει μεγάλες τιμές (μας αρκεί  )
) , λόγω παρονομαστή, πρέπει να την δούμε χωριστά: Σε αυτή την περίπτωση η μεν εφαπτομένη στο γράφημα είναι οριζόντια το δε διάστημα με άκρα
, λόγω παρονομαστή, πρέπει να την δούμε χωριστά: Σε αυτή την περίπτωση η μεν εφαπτομένη στο γράφημα είναι οριζόντια το δε διάστημα με άκρα  είναι κατακόρυφο. Άρα πάλι έχουμε την ζητούμενη καθετότητα.
είναι κατακόρυφο. Άρα πάλι έχουμε την ζητούμενη καθετότητα. , οπότε σε κάθε σημείο της
, οπότε σε κάθε σημείο της  δέχεται εφαπτομένη
δέχεται εφαπτομένη  , (που δεν είναι κάθετη στον οριζόντιο άξονα).
, (που δεν είναι κάθετη στον οριζόντιο άξονα). , με σημείο τομής
, με σημείο τομής  . Τότε, είτε σχηματίζεται ορθογώνιο τρίγωνο
. Τότε, είτε σχηματίζεται ορθογώνιο τρίγωνο  , είτε η εφαπτομένη
, είτε η εφαπτομένη  (δηλαδή ταυτίζονται τα
(δηλαδή ταυτίζονται τα  ), είτε ταυτίζονται τα
), είτε ταυτίζονται τα  , οπότε στο
, οπότε στο  έχουμε
έχουμε  .
. , ενώ στην τρίτη έχουμε
, ενώ στην τρίτη έχουμε  .
.  , με το «ίσον» όταν ταυτίζονται. Αν δεν υπήρχαν τέτοια σημεία, τότε το
, με το «ίσον» όταν ταυτίζονται. Αν δεν υπήρχαν τέτοια σημεία, τότε το  που απέχει την ελάχιστη απόσταση
που απέχει την ελάχιστη απόσταση  .
. με το ίσον όταν ταυτίζονται, άρα
με το ίσον όταν ταυτίζονται, άρα  .
. είναι
είναι  που ταυτίζεται με το κάποιο από τα σημεία
που ταυτίζεται με το κάποιο από τα σημεία  .
. , για κάθε
, για κάθε  .
.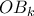 είναι
είναι  , οπότε το
, οπότε το  στο διάστημα
στο διάστημα  , όπου
, όπου  από την αρχή των αξόνων και
από την αρχή των αξόνων και  η συνάρτηση του ημικύκλιο ακτίνας
η συνάρτηση του ημικύκλιο ακτίνας  γιατί διαφορετικά θα υπήρχε σημείο
γιατί διαφορετικά θα υπήρχε σημείο  . Δηλαδή το σημείο
. Δηλαδή το σημείο  θα ήταν εσωτερικό του κύκλου και η απόσταση από το
θα ήταν εσωτερικό του κύκλου και η απόσταση από το  είναι παραγωγίσιμη ως άθροισμα παραγωγίσιμων συναρτήσεων. Και επειδή τα σημεία ελαχίστου απόστασης
είναι παραγωγίσιμη ως άθροισμα παραγωγίσιμων συναρτήσεων. Και επειδή τα σημεία ελαχίστου απόστασης  είναι και σημεία στα οποία η
είναι και σημεία στα οποία η  , από το θεώρημα του Fermat θα είναι
, από το θεώρημα του Fermat θα είναι  . Η εφαπτομένη όμως της
. Η εφαπτομένη όμως της  να ταυτίζονται.
να ταυτίζονται.
 έχει ελάχιστο .
έχει ελάχιστο . τότε μπορεί να γίνει.
τότε μπορεί να γίνει.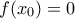 (στο
(στο 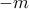 ) δε ξέρω αν σώζεται κάπως έτσι: Είναι
) δε ξέρω αν σώζεται κάπως έτσι: Είναι
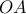 κάθετο προς την εφαπτομένη. Ομοίως στην άλλη άκρη του ημικυκλίου. Έχοντας υπόψη δυο περιπτώσεις για την
κάθετο προς την εφαπτομένη. Ομοίως στην άλλη άκρη του ημικυκλίου. Έχοντας υπόψη δυο περιπτώσεις για την