 , για την οποία ισχύει
, για την οποία ισχύει 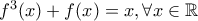 και ότι
και ότι 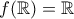 .
.Να υπολογισθεί το
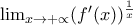 .
.Υ.Γ Η παραγωγισιμότητα και το σύνολο τιμών της
 θα μπορούσαν να μη δίνονται ως δεδομένα
θα μπορούσαν να μη δίνονται ως δεδομέναΣυντονιστής: Μπάμπης Στεργίου
 , για την οποία ισχύει
, για την οποία ισχύει 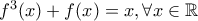 και ότι
και ότι 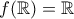 .
.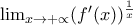 .
. θα μπορούσαν να μη δίνονται ως δεδομένα
θα μπορούσαν να μη δίνονται ως δεδομέναChatzibill έγραψε: ↑Κυρ Δεκ 16, 2018 6:31 pmΔίνεται η παραγωγίσιμη συνάρτηση, για την οποία ισχύει
και ότι
.
Να υπολογισθεί το.
Υ.Γ Η παραγωγισιμότητα και το σύνολο τιμών τηςθα μπορούσαν να μη δίνονται ως δεδομένα
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  , τότε παραγωγίζοντας τη σχέση που μας δίδεται έχουμε:
, τότε παραγωγίζοντας τη σχέση που μας δίδεται έχουμε: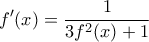


Πιο απλά: ΓιαChatzibill έγραψε: ↑Κυρ Δεκ 16, 2018 6:31 pmΔίνεται η παραγωγίσιμη συνάρτηση, για την οποία ισχύει
και ότι
.
Να υπολογισθεί το.
Υ.Γ Η παραγωγισιμότητα και το σύνολο τιμών τηςθα μπορούσαν να μη δίνονται ως δεδομένα
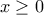 είναι προφανώς
είναι προφανώς  άρα
άρα 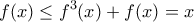 . Έχουμε
. Έχουμε 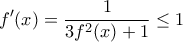 και για
και για  είναι
είναι 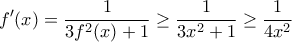 . Άρα
. Άρα 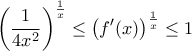 .
.  τα δύο άκρα τείνουν στο
τα δύο άκρα τείνουν στο  , άρα και το ζητούμενο όριο είναι
, άρα και το ζητούμενο όριο είναι  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες