αύξουσα και συνεχής
Δημοσιεύτηκε: Κυρ Δεκ 16, 2018 3:31 pm
Να αποδειχτεί ότι κάθε συνεχής και αύξουσα συνάρτηση  , τέμνει την ευθεία
, τέμνει την ευθεία  σε ένα ακριβώς σημείο.
σε ένα ακριβώς σημείο.
 , τέμνει την ευθεία
, τέμνει την ευθεία  σε ένα ακριβώς σημείο.
σε ένα ακριβώς σημείο. , τέμνει την ευθεία
, τέμνει την ευθεία  σε ένα ακριβώς σημείο.
σε ένα ακριβώς σημείο.Η συνάρτησηChatzibill έγραψε: ↑Κυρ Δεκ 16, 2018 3:31 pmΝα αποδειχτεί ότι κάθε συνεχής και αύξουσα συνάρτηση, τέμνει την ευθεία
σε ένα ακριβώς σημείο.
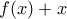 είναι γνήσια αύξουσα ως άθροισμα μιας αύξουσα και μιας γνήσια αύξουσας (*). Άρα η ισοδύναμη εξίσωση
είναι γνήσια αύξουσα ως άθροισμα μιας αύξουσα και μιας γνήσια αύξουσας (*). Άρα η ισοδύναμη εξίσωση  έχει το πολύ μία ρίζα. Θα δείξουμε ότι, επίσης, έχει τουλάχιστον μία ρίζα, οπότε τελειώσαμε.
έχει το πολύ μία ρίζα. Θα δείξουμε ότι, επίσης, έχει τουλάχιστον μία ρίζα, οπότε τελειώσαμε.  , τότε δεν έχουμε τίποτα να απoδείξουμε αφού γράφεται
, τότε δεν έχουμε τίποτα να απoδείξουμε αφού γράφεται  . Οπότε μπορούμε να υποθέσουμε ότι
. Οπότε μπορούμε να υποθέσουμε ότι  (η περίπτωση
(η περίπτωση  όμοια). Για τον αρνητικό αριθμό
όμοια). Για τον αρνητικό αριθμό  ισχύει από την υπόθεση ότι
ισχύει από την υπόθεση ότι 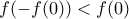 άρα
άρα  . Από Bolzano στο
. Από Bolzano στο ![[-f(0), 0] [-f(0), 0]](/forum/ext/geomar/texintegr/latexrender/pictures/c26aa5498f4d5ecc505ed5393995832c.png) στην συνεχή
στην συνεχή 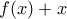 έπεται το ζητούμενο.
έπεται το ζητούμενο. αρκεί να είναι (απλά) αύξουσα, όπως στην υπόθεση, οπότε έκανα διορθωσούλα.
αρκεί να είναι (απλά) αύξουσα, όπως στην υπόθεση, οπότε έκανα διορθωσούλα.  ως γνησίως αύξουσα και συνεχής θα έχει σύνολο τιμών
ως γνησίως αύξουσα και συνεχής θα έχει σύνολο τιμών  , προφανώς (αφού ορίζεται διάστημα)
, προφανώς (αφού ορίζεται διάστημα)  .
. τότε και
τότε και  που σημαίνει
που σημαίνει 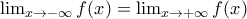 , άτοπο.
, άτοπο. , παρόμοια
, παρόμοια 
 η
η  είναι γνησίως αύξουσα και συνεχής, άρα λαμβάνοντας υπόψιν τα παραπάνω έχει σύνολο τιμών :
είναι γνησίως αύξουσα και συνεχής, άρα λαμβάνοντας υπόψιν τα παραπάνω έχει σύνολο τιμών :
 υπάρχει
υπάρχει  τέτοιος ώστε
τέτοιος ώστε  .
. ως γνησίως μονότονη θα είναι και
ως γνησίως μονότονη θα είναι και  συνάρτηση , άρα
συνάρτηση , άρα  μοναδικός αριθμός.
μοναδικός αριθμός. είναι γνησίως αύξουσα αντί για αύξουσα συνάρτηση. Μετά από την παρατήρηση του Σταύρου Παπαδόπουλου σε επόμενο ποστ έχει γραφεί αναλυτική λύση στα δεδομένα της άσκησης.
είναι γνησίως αύξουσα αντί για αύξουσα συνάρτηση. Μετά από την παρατήρηση του Σταύρου Παπαδόπουλου σε επόμενο ποστ έχει γραφεί αναλυτική λύση στα δεδομένα της άσκησης.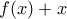 είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα. .
.

 είναι
είναι 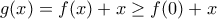



 Η
Η  είναι αύξουσα και συνεχή αρα 1-1 δηλαδή αντιστρέψιμη στο σύνολο τιμών της
είναι αύξουσα και συνεχή αρα 1-1 δηλαδή αντιστρέψιμη στο σύνολο τιμών της 
 θα έχει σύνολο τιμών το
θα έχει σύνολο τιμών το  kai το ίδιο θα συμβαίνει στην 2η περίπτωση διότι είναι αύξουσα
kai το ίδιο θα συμβαίνει στην 2η περίπτωση διότι είναι αύξουσα τότε
τότε 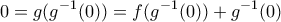 ή
ή 
 στο
στο ![\displaystyle{[0,g^{-1}(0)]} \displaystyle{[0,g^{-1}(0)]}](/forum/ext/geomar/texintegr/latexrender/pictures/e5daa377988f28049f1bbf95426d63c9.png) η
η  έχει ρίζα μοναδική λόγω μονοτονίας
έχει ρίζα μοναδική λόγω μονοτονίας η
η  είναι γνησίως αύξουσα και συνεχής.
είναι γνησίως αύξουσα και συνεχής. για κάθε
για κάθε  και συνεχής γιατί είναι άθροισμα συνεχών συναρτήσεων.
και συνεχής γιατί είναι άθροισμα συνεχών συναρτήσεων. είναι
είναι 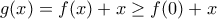
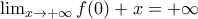 συνεπώς
συνεπώς 


 υπάρχει
υπάρχει  τέτοιος ώστε
τέτοιος ώστε  .
. ως γνησίως μονότονη θα είναι και
ως γνησίως μονότονη θα είναι και  συνάρτηση , άρα
συνάρτηση , άρα  μοναδικός αριθμός.
μοναδικός αριθμός.από το παραπάνω , με το λίγο που το επεξεργάστηκα κοιτάζοντας πριν αυτό:
Νομίζω ότι είναι αρκετά προκλητικό να αποδείξουμε ότι :ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Δεκ 16, 2018 6:12 pm... να μην χρησιμοποιήσουμε το βαρύ για σχολικά μαθηματικά
αύξουσα συνάρτηση συνεχής έχει όριο. ...
Ανάυξουσα και συνεχής συνάρτηση στο
τότε τα όρια
υπάρχουν.
Μόνο με χρήση σχολικών μαθηματικών
Το παραπάνω είναι ισοδύναμο με το Αξίωμα Πληρότητας για άμεσο λόγο. Οπότε για Σχολικά Μαθηματικά μπαίνουμε σε δύσκολα χωράφια (γι' αυτό άλλωστε ο Σταύρος μίλησε για "βαρύ για σχολικά μαθηματικά εργαλείο")Christos.N έγραψε: ↑Κυρ Δεκ 16, 2018 7:01 pmΝομίζω ότι είναι αρκετά προκλητικό να αποδείξουμε ότι :
Ανάυξουσα και συνεχής συνάρτηση στο
τότε τα όρια
υπάρχουν.
Μόνο με χρήση σχολικών μαθηματικών