
Χαμός στο ίσιωμα
Συντονιστής: Μπάμπης Στεργίου
Χαμός στο ίσιωμα
Να μελετηθεί ως προς την κυρτότητα και τα σημεία καμπής η συνάρτηση :


Λέξεις Κλειδιά:
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Χαμός στο ίσιωμα
Καταρχάς θέλουμε
 . Από τα παρακάτω θα διαπιστώσουμε ότι δεν υπάρχει άλλος περιορισμός.
. Από τα παρακάτω θα διαπιστώσουμε ότι δεν υπάρχει άλλος περιορισμός.H αριστερή παράσταση είναι

Όμοια η δεξιά

Εύκολα τώρα βλέπουμε ότι η
 στο
στο ![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png) ισούται
ισούται  που είναι γνήσια φθίνουσα και κυρτή (από την αντίστοιχη ιδιότητα της
που είναι γνήσια φθίνουσα και κυρτή (από την αντίστοιχη ιδιότητα της 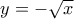 )
)Στο
![[3,6] [3,6]](/forum/ext/geomar/texintegr/latexrender/pictures/040d10f86154a1502dd90b06a19ded59.png) είναι σταθερή
είναι σταθερή  (εξ ου και ο ευρηματικός τίτλος), και στο
(εξ ου και ο ευρηματικός τίτλος), και στο  είναι
είναι  , δηλαδή γνήσια αύξουσα και κοίλη (από την αντίστοιχη ιδιότητα της
, δηλαδή γνήσια αύξουσα και κοίλη (από την αντίστοιχη ιδιότητα της  ).
).Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες
