Christos.N έγραψε:Tolaso J Kos έγραψε:
(γ.ιι) 
 Δε τα βλέπω αυτή τη στιγμή.
Δε τα βλέπω αυτή τη στιγμή.
Λήμμα
Αν

γνησίως αύξουσα και αντιστρέψιμη συνάρτηση , τότε και

γνησίως αύξουσα συνάρτηση.
Απόδειξη:
 Παρατήρηση-υπόδειξη :
Παρατήρηση-υπόδειξη : 
Ξέχασα:
M.S.Vovos έγραψε:
(γ.ii.) Να λύσετε τις παρακάτω εξισώσεις, όταν
![\displaystyle{x\in \left [ 1-\ln 2,1+\ln 2 \right ]} \displaystyle{x\in \left [ 1-\ln 2,1+\ln 2 \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/ae3a0efc6a63088a6199eca0ad421d35.png)
:

Συνηθίζεται να δίνεται το κοινό πεδίο ορισμού των συναρτήσεων.
Καλησπέρα. Μια, καθαρά γεωμετρική εντός σχολικού πλαισίου, προσπάθεια για το (γ)(ii)...
Είναι:



(1)
Ισχύει :

. Συνεπώς η

είναι γνησίως αύξουσα στο
![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png)
.
Επίσης
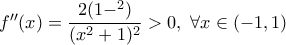
. Συνεπώς η

είναι κυρτή στο
![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png)
.
Επί πλέον η εφαπτομένη της γραφικής παράστασης της συνάρτησης

στο σημείο

είναι η

.
Επομένως η γραφική παράσταση της συνάρτησης

βρίσκεται πάνω από την

, εκτός από το σημείο επαφής.
Ακόμα γνωρίζουμε ότι η γραφική παράσταση της συνάρτησης

, είναι συμμετρική της

με άξονα συμμετρίας την

. Συνεπώς, λόγω της συμμετρίας αυτής, εφάπτεται και αυτή στο σημείο

,βρίσκεται κάτω από την

, εκτός από το σημείο επαφής.
Από τα παραπάνω προκύπτει

και

, για κάθε

, στο
![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png)
.
Συνεπώς μοναδική λύση της (1) είναι η

. Ομοίως εργαζόμαστε και για την δεύτερη.
Φιλικά
Σταμ. Γλάρος
![f:\left [ -1,1 \right ]\rightarrow \mathbb{R} f:\left [ -1,1 \right ]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/2ae83dd8241dcab1e12883d1d670589d.png) , παραγωγίσιμη στο
, παραγωγίσιμη στο  τέτοια ώστε:
τέτοια ώστε:

 , για κάθε
, για κάθε 
 ,
, ![x\in [-1,1] x\in [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/547db7d2339cfb3345123313fe6a4981.png) .
. είναι γνησίως αύξουσα και να βρείτε το μέγιστο της συνάρτησης
είναι γνησίως αύξουσα και να βρείτε το μέγιστο της συνάρτησης  .
. είναι αντιστρέψιμη στο πεδίο ορισμού της και να βρείτε το πεδίο ορισμού της συνάρτησης
είναι αντιστρέψιμη στο πεδίο ορισμού της και να βρείτε το πεδίο ορισμού της συνάρτησης  .
.![\displaystyle{x\in \color{red} \left [\ln 2 -1,1 \right ]} \displaystyle{x\in \color{red} \left [\ln 2 -1,1 \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/10d9af81152c8b8caade2f56b4af7eb4.png) :
: (δ) Να υπολογίσετε το εμβαδόν του χωρίου
(δ) Να υπολογίσετε το εμβαδόν του χωρίου  , που περικλείεται από τη γραφική παράσταση της συνάρτησης
, που περικλείεται από τη γραφική παράσταση της συνάρτησης  , τους άξονες συντεταγμένων και την ευθεία
, τους άξονες συντεταγμένων και την ευθεία  , αν γνωρίζετε ότι:
, αν γνωρίζετε ότι: Φιλικά,
Φιλικά,
![\displaystyle{x\in \left [ 1-\ln 2,1+\ln 2 \right ]} \displaystyle{x\in \left [ 1-\ln 2,1+\ln 2 \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/ae3a0efc6a63088a6199eca0ad421d35.png) :
: .
. , συνεχής στο
, συνεχής στο ![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) ως πράξεις συνεχών συναρτήσεων
ως πράξεις συνεχών συναρτήσεων ![[-1,x] [-1,x]](/forum/ext/geomar/texintegr/latexrender/pictures/7d9545bd832d65903b86a65afc737287.png) , υπάρχει τουλάχιστον ένα
, υπάρχει τουλάχιστον ένα  τέτοιο ώστε :
τέτοιο ώστε : λόγω της (1).
λόγω της (1). (2).
(2).![[x,1] [x,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e6689e594cced63960b4f18d29966070.png) , υπάρχει τουλάχιστον ένα
, υπάρχει τουλάχιστον ένα  τέτοιο ώστε :
τέτοιο ώστε :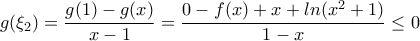 λόγω της (1).
λόγω της (1). (3).
(3). .
. η οποία είναι παραγωγίσιμη στο
η οποία είναι παραγωγίσιμη στο ![[-1, 1] [-1, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/7dec1d46e68831c4eca28b020fcb1604.png) με
με  από την υπόθεση. Συνεπώς η
από την υπόθεση. Συνεπώς η  είναι φθίνουσα. Επειδή είναι ορισμένη σε κλειστό διάστημα θα παίρνει ως μονότονη μέγιστη και ελάχιστη τιμή στο
είναι φθίνουσα. Επειδή είναι ορισμένη σε κλειστό διάστημα θα παίρνει ως μονότονη μέγιστη και ελάχιστη τιμή στο  και στο
και στο  αντίστοιχα. Τότε
αντίστοιχα. Τότε
 για κάθε
για κάθε ![x \in [-1, 1] x \in [-1, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/d4c38ceb76ab070c6884a3a5f5a00c19.png) και κατά συνέπεια
και κατά συνέπεια ![f(x) = x + \ln \left(x^2+1 \right) \;\; x \in [-1, 1] f(x) = x + \ln \left(x^2+1 \right) \;\; x \in [-1, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/6a0957cd601dab851e62d0fa06c53289.png) .
. με την ισότητα να ισχύει μόνο για
με την ισότητα να ισχύει μόνο για  . Κατά συνέπεια η
. Κατά συνέπεια η 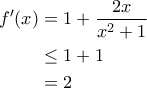

![[f(-1), f(1)] [f(-1), f(1)]](/forum/ext/geomar/texintegr/latexrender/pictures/c6b226dab0380e0149bd318443225b20.png) δηλ. το σύνολο
δηλ. το σύνολο![\displaystyle{\mathcal{R} = \left [ \ln 2 -1 , 1 + \ln 2 \right ]} \displaystyle{\mathcal{R} = \left [ \ln 2 -1 , 1 + \ln 2 \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/278af3eed0038f0372e9a0949e64bc51.png)
 είναι
είναι  αφού
αφού ![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \left [ x + \ln \left ( x^2+1 \right ) \right ] \, {\rm d}x \\
&=\frac{1}{2} + \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x \\
&= \frac{1}{2} + \left [ x \ln \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x\\
&= \frac{1}{2} + \ln 2 - 2\int_{0}^{1} \left ( 1 - \frac{1}{x^2+1} \right ) \, {\rm d}x\\
&= \frac{1}{2} +\ln 2 - 2 + \int_{-1}^{1} \frac{{\rm d}x}{x^2+1} \\
&= \ln 2 + \frac{\pi}{2} - \frac{3}{2}
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1} \left [ x + \ln \left ( x^2+1 \right ) \right ] \, {\rm d}x \\
&=\frac{1}{2} + \int_{0}^{1} \ln \left ( x^2+1 \right ) \, {\rm d}x \\
&= \frac{1}{2} + \left [ x \ln \left ( x^2+1 \right ) \right ]_0^1 - 2\int_{0}^{1} \frac{x^2}{x^2+1} \, {\rm d}x\\
&= \frac{1}{2} + \ln 2 - 2\int_{0}^{1} \left ( 1 - \frac{1}{x^2+1} \right ) \, {\rm d}x\\
&= \frac{1}{2} +\ln 2 - 2 + \int_{-1}^{1} \frac{{\rm d}x}{x^2+1} \\
&= \ln 2 + \frac{\pi}{2} - \frac{3}{2}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/04c394e6c8849ff7150e8ba1dd7772dc.png)

 γνησίως αύξουσα συνάρτηση.
γνησίως αύξουσα συνάρτηση.

 .
. είναι φθίνουσα με την ίδια τιμή 0 στα άκρα -1 και 1 άρα είναι η σταθερή συνάρτηση 0 οπότε
είναι φθίνουσα με την ίδια τιμή 0 στα άκρα -1 και 1 άρα είναι η σταθερή συνάρτηση 0 οπότε 


 (1)
(1) . Συνεπώς η
. Συνεπώς η 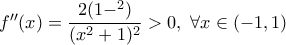 . Συνεπώς η
. Συνεπώς η  είναι η
είναι η  .
. ,βρίσκεται κάτω από την
,βρίσκεται κάτω από την  και
και  , για κάθε
, για κάθε  , στο
, στο  . Ομοίως εργαζόμαστε και για την δεύτερη.
. Ομοίως εργαζόμαστε και για την δεύτερη. δεν ανήκει στο διάστημα που ορίζεται η μεταβλητή
δεν ανήκει στο διάστημα που ορίζεται η μεταβλητή  .
. είναι για την συνάρτηση
είναι για την συνάρτηση 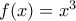 αφού
αφού  και είναι γνήσια αύξουσα…
και είναι γνήσια αύξουσα…  να βγάζουν συμπεράσματα για
να βγάζουν συμπεράσματα για ![x\in \left[ -1+\ln 2,\,1+\ln 2 \right] x\in \left[ -1+\ln 2,\,1+\ln 2 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/0ec6d02bb23bd6fbb3ecb9f9d51cd847.png) οπότε η γεωμετρική προσέγγιση του
οπότε η γεωμετρική προσέγγιση του ![[-1+\ln 2,\, 1] [-1+\ln 2,\, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/a751afc22947f322021b88c159676e37.png) .
.![\displaystyle{\left[ {1 - \ln 2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1} \right]} \displaystyle{\left[ {1 - \ln 2{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/fcccfce31272e1b4b56cfc6e6a3522af.png) όπου
όπου  , άρα μετά την όποια προσέγγιση (δική σου (κυρότητα)
, άρα μετά την όποια προσέγγιση (δική σου (κυρότητα) ![f([-1,1])=[f(-1),f(1)]=[-1+\ln 2,1+\ln 2] f([-1,1])=[f(-1),f(1)]=[-1+\ln 2,1+\ln 2]](/forum/ext/geomar/texintegr/latexrender/pictures/95f519ee766a6a49f0d14e6546dc41ee.png) για την εξίσωση την λύνουμε στο κοινό πεδίο ορισμού που εδώ είναι
για την εξίσωση την λύνουμε στο κοινό πεδίο ορισμού που εδώ είναι ![[-1+\ln 2,\,\,1+\ln 2]\cap [-1,\,\,1]=[-1+ln2,\,\,1] [-1+\ln 2,\,\,1+\ln 2]\cap [-1,\,\,1]=[-1+ln2,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/696fd2a9f059dc9db1d3274f3c5f99b6.png) που από αβλεψία μου είχα γράψει και εγώ λάθος το δεξί άκρο….
που από αβλεψία μου είχα γράψει και εγώ λάθος το δεξί άκρο….![0\in \left[ -1+\ln 2,\,1 \right] 0\in \left[ -1+\ln 2,\,1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/9d851cfba4287eb8b241ea544d01aff4.png) Αν τώρα υπάρχει
Αν τώρα υπάρχει 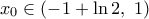 με
με 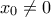 ώστε
ώστε  (1) λόγω κυρτότητας θα είναι
(1) λόγω κυρτότητας θα είναι 
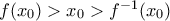 και από (1)
και από (1)  που είναι άτοπο λόγω του προηγουμένου
που είναι άτοπο λόγω του προηγουμένου με την ισότητα να ισχύει μόνο για
με την ισότητα να ισχύει μόνο για  είναι
είναι 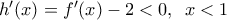 δηλαδή είναι γνήσια φθίνουσα , έτσι αφού ισχύει
δηλαδή είναι γνήσια φθίνουσα , έτσι αφού ισχύει  θα ισχύει ότι
θα ισχύει ότι 

 . Έτσι βλέπουμε ότι η μοναδική λύση που επαληθεύει είναι η
. Έτσι βλέπουμε ότι η μοναδική λύση που επαληθεύει είναι η  , για κάθε
, για κάθε  αλλά για
αλλά για  ;
;