Μέγιστο εμβαδόν
Συντονιστής: Μπάμπης Στεργίου
- Christos.N
- Δημοσιεύσεις: 2105
- Εγγραφή: Πέμ Νοέμ 26, 2009 2:28 pm
- Τοποθεσία: Ίλιον
Μέγιστο εμβαδόν
Στο παρακάτω σχήμα το οποίο παριστάνει έλλειψη κατασκευάσαμε ένα τρίγωνο του οποίου η μια κορυφή βρίσκεται σε μια εστία της οι άλλες δύο στην έλλειψη, ενώ η απέναντι πλευρά διέρχεται από την έτερη εστία της. Ζητάμε την κατάλληλη θέση του τριγώνου ώστε να πετυχαίνουμε το μέγιστο εμβαδόν.
Η επιλογή του φακέλου , θέλει να δείξει ότι μπορούμε να μεταχειριστούμε οποιοδήποτε εργαλείο χρειαζόμαστε.
Η επιλογή του φακέλου , θέλει να δείξει ότι μπορούμε να μεταχειριστούμε οποιοδήποτε εργαλείο χρειαζόμαστε.
Χρήστος Ντάβας
Wir müssen wissen — wir werden wissen! D.Hilbert
Wir müssen wissen — wir werden wissen! D.Hilbert
Λέξεις Κλειδιά:
Re: Μέγιστο εμβαδόν
Προφανώς  , συνεπώς
, συνεπώς  , με το υπόρριζο να
, με το υπόρριζο να
μεγιστοποιείται για (γιατί ; ) , δηλαδή όταν η
(γιατί ; ) , δηλαδή όταν η  είναι κάθετη στην
είναι κάθετη στην 
Η λύση αποσύρεται : Η μεγιστοποίηση δεν επιτυγχάνεται για :
 , συνεπώς
, συνεπώς  , με το υπόρριζο να
, με το υπόρριζο ναμεγιστοποιείται για
 (γιατί ; ) , δηλαδή όταν η
(γιατί ; ) , δηλαδή όταν η  είναι κάθετη στην
είναι κάθετη στην 
Η λύση αποσύρεται : Η μεγιστοποίηση δεν επιτυγχάνεται για :

τελευταία επεξεργασία από KARKAR σε Σάβ Νοέμ 14, 2020 9:25 am, έχει επεξεργασθεί 2 φορές συνολικά.
- ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
- Επιμελητής
- Δημοσιεύσεις: 4658
- Εγγραφή: Κυρ Μαρ 13, 2011 9:11 pm
- Τοποθεσία: Βρυξέλλες
Re: Μέγιστο εμβαδόν
Καλησπέρα Χρήστο με το όμορφο αυτό πρόβλημα που έχει και όμορφη διερεύνηση δεν θέλει βιασύνηChristos.N έγραψε:Στο παρακάτω σχήμα το οποίο παριστάνει έλλειψη κατασκευάσαμε ένα τρίγωνο του οποίου η μια κορυφή βρίσκεται σε μια εστία της οι άλλες δύο στην έλλειψη, ενώ η απέναντι πλευρά διέρχεται από την έτερη εστία της. Ζητάμε την κατάλληλη θέση του τριγώνου ώστε να πετυχαίνουμε το μέγιστο εμβαδόν.Η επιλογή του φακέλου , θέλει να δείξει ότι μπορούμε να μεταχειριστούμε οποιοδήποτε εργαλείο χρειαζόμαστε.
Καταγραφή4.PNG
 Αν το
Αν το  είναι δεν είναι εξωτερικό σημείο του κύκλου με κέντρο το κέντρο της έλλειψης και διάμετρος το μικρό άξονα (δηλαδή αν ισχύει :
είναι δεν είναι εξωτερικό σημείο του κύκλου με κέντρο το κέντρο της έλλειψης και διάμετρος το μικρό άξονα (δηλαδή αν ισχύει :  (με
(με  και
και  το μήκος του μεγάλου άξονα της έλλειψης, τότε το αποτέλεσμα είναι αυτό που γράφει ο Θανάσης.
το μήκος του μεγάλου άξονα της έλλειψης, τότε το αποτέλεσμα είναι αυτό που γράφει ο Θανάσης.  Αν όμως το
Αν όμως το  τότε τα
τότε τα  για την μεγιστοποίηση του εμβαδού είναι τα σημεία τομής της (των , δύο λύσεις) εφαπτομένων ευθειών που διέρχονται από το
για την μεγιστοποίηση του εμβαδού είναι τα σημεία τομής της (των , δύο λύσεις) εφαπτομένων ευθειών που διέρχονται από το  στον κύκλο με κέντρο το της έλλειψης και διάμετρο το μικρό άξονα .
στον κύκλο με κέντρο το της έλλειψης και διάμετρο το μικρό άξονα . Η απόδειξη γίνεται με αρκετούς τρόπους και σωστά ο Χρήστος το τοποθέτησε στο φάκελο αυτό. Μια όμορφη απόδειξη (με λογιστικό περιεχόμενο) είναι με τη διευθετούσα της έλλειψης που αντιστοιχεί στην εστία
 ΄(με εξίσωση :
΄(με εξίσωση :  (στη δεύτερη περίπτωση που έχει και το ιδιαίτερο ενδιαφέρον ) αδιαφορώντας για τις εφαπτόμενες που περιγράφω πιο πάνω , αντιμετωπίζοντας το θέμα μόνο λογιστικά αφού οι εφαπτόμενες της έλλειψης στα σημεία
(στη δεύτερη περίπτωση που έχει και το ιδιαίτερο ενδιαφέρον ) αδιαφορώντας για τις εφαπτόμενες που περιγράφω πιο πάνω , αντιμετωπίζοντας το θέμα μόνο λογιστικά αφού οι εφαπτόμενες της έλλειψης στα σημεία  , με
, με 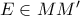 τέμνονται επί της
τέμνονται επί της  (δηλαδή η
(δηλαδή η  είναι (διερχόμενη από την εστία
είναι (διερχόμενη από την εστία  της έλλειψης) η πολική τυχόντος σημείου της
της έλλειψης) η πολική τυχόντος σημείου της  ) γνωστή πρόταση ζητώντας τη μεγιστοποίησης της ορθής προβολής του
) γνωστή πρόταση ζητώντας τη μεγιστοποίησης της ορθής προβολής του  επί της
επί της  , δηλαδή τη μεγιστοποίηση του
, δηλαδή τη μεγιστοποίηση του  αφού είναι προφανές ότι το
αφού είναι προφανές ότι το  επιτυγχάνεται (βλέποντάς το ως το άθροισμα
επιτυγχάνεται (βλέποντάς το ως το άθροισμα  (με κοινή βάση της
(με κοινή βάση της  ) όταν
) όταν  (το άθροισμα των υψών του) γίνει μέγιστο
(το άθροισμα των υψών του) γίνει μέγιστοΣτάθης
Υ.Σ. Θα επανέλθω αύριο αν βρώ χρόνο για τις λεπτομέρειες
Τι περιμένετε λοιπόν ναρθεί , ποιόν καρτεράτε να σας σώσει.
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
Re: Μέγιστο εμβαδόν
Η έλλειψη του σχήματος έχει : 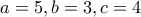 , δηλαδή ισχύει το :
, δηλαδή ισχύει το :  και πράγματι
και πράγματι
το μέγιστο επιτυγχάνεται όταν το είναι το σημείο τομής της εφαπτομένης από την
είναι το σημείο τομής της εφαπτομένης από την 
προς τον κύκλο με διάμετρο τον μικρό άξονα , όπως σωστά επισημαίνει ο Στάθης .
Ο τύπος του εμβαδού ( ) , που έδωσα στην πρώτη μου ανάρτηση
) , που έδωσα στην πρώτη μου ανάρτηση
είναι σωστός . Το λάθος λοιπόν βρίσκεται στον ισχυρισμό , ότι η μεγιστοποίηση επιτυγχάνεται
όταν . Αυτό το θεώρησα προφανές και θα ίσχυε όντως , αν αντί για έλλειψη
. Αυτό το θεώρησα προφανές και θα ίσχυε όντως , αν αντί για έλλειψη
είχαμε κύκλο , οπότε το θα ήταν σταθερό , ενώ το
θα ήταν σταθερό , ενώ το  θα γίνονταν
θα γίνονταν
ελάχιστο αν . Στην έλλειψη όμως αυτό δεν ισχύει ...
. Στην έλλειψη όμως αυτό δεν ισχύει ... 
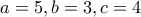 , δηλαδή ισχύει το :
, δηλαδή ισχύει το :  και πράγματι
και πράγματιτο μέγιστο επιτυγχάνεται όταν το
 είναι το σημείο τομής της εφαπτομένης από την
είναι το σημείο τομής της εφαπτομένης από την 
προς τον κύκλο με διάμετρο τον μικρό άξονα , όπως σωστά επισημαίνει ο Στάθης .
Ο τύπος του εμβαδού (
 ) , που έδωσα στην πρώτη μου ανάρτηση
) , που έδωσα στην πρώτη μου ανάρτηση είναι σωστός . Το λάθος λοιπόν βρίσκεται στον ισχυρισμό , ότι η μεγιστοποίηση επιτυγχάνεται
όταν
 . Αυτό το θεώρησα προφανές και θα ίσχυε όντως , αν αντί για έλλειψη
. Αυτό το θεώρησα προφανές και θα ίσχυε όντως , αν αντί για έλλειψηείχαμε κύκλο , οπότε το
 θα ήταν σταθερό , ενώ το
θα ήταν σταθερό , ενώ το  θα γίνονταν
θα γίνοντανελάχιστο αν
 . Στην έλλειψη όμως αυτό δεν ισχύει ...
. Στην έλλειψη όμως αυτό δεν ισχύει ... - ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
- Επιμελητής
- Δημοσιεύσεις: 4658
- Εγγραφή: Κυρ Μαρ 13, 2011 9:11 pm
- Τοποθεσία: Βρυξέλλες
Re: Μέγιστο εμβαδόν
Τελικά αποφάσισα να δώσω μια λύση και για τις δύο περιπτώσεις όπως προκύπτει από τη διερεύνησηChristos.N έγραψε:Στο παρακάτω σχήμα το οποίο παριστάνει έλλειψη κατασκευάσαμε ένα τρίγωνο του οποίου η μια κορυφή βρίσκεται σε μια εστία της οι άλλες δύο στην έλλειψη, ενώ η απέναντι πλευρά διέρχεται από την έτερη εστία της. Ζητάμε την κατάλληλη θέση του τριγώνου ώστε να πετυχαίνουμε το μέγιστο εμβαδόν.
Η επιλογή του φακέλου , θέλει να δείξει ότι μπορούμε να μεταχειριστούμε οποιοδήποτε εργαλείο χρειαζόμαστε.
Καταγραφή4.PNG
Έστω
 (διερχόμενη από την εστία
(διερχόμενη από την εστία  της έλλειψης
της έλλειψης  .
.Τότε οι συντεταγμένες των
 θα προκύψουν από τη λύση του συστήματος
θα προκύψουν από τη λύση του συστήματος 


Η εξίσωση
 έχει ρίζες
έχει ρίζες  (τις τεταγμένες των
(τις τεταγμένες των  αντίστοιχα) με
αντίστοιχα) με  και
και 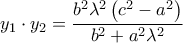
Με


 και επομένως η μεγιστοποίησή του θα προκύψει (αφού
και επομένως η μεγιστοποίησή του θα προκύψει (αφού  παραμένει σταθερό αν μεγιστοποιηθεί η παράσταση
παραμένει σταθερό αν μεγιστοποιηθεί η παράσταση  ή ισοδύναμα η παράσταση
ή ισοδύναμα η παράσταση 


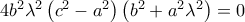




 .
.Για να έχει η
 δύο ρίζες ως προς
δύο ρίζες ως προς  πρέπει η διακρίνουσα
πρέπει η διακρίνουσα 
![{\left[ {2\left( {{a^2}{b^2}k - 2{a^2}{b^4}} \right)} \right]^2} - {\left[ {2\left( {{a^2}{b^2}k - 2{a^2}{b^4}} \right)} \right]^2} -](/forum/ext/geomar/texintegr/latexrender/pictures/0545e46e5782a07dccd26e148b62e149.png)


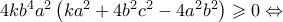


 .
.Με
 για
για 


 . Αρα
. Αρα 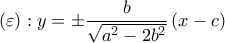 .
.Αν
 τότε η εξίσωση
τότε η εξίσωση  είναι αδύνατη ως προς
είναι αδύνατη ως προς  άρα και ως προς
άρα και ως προς  και συνεπώς η ζητούμενη ευθεία δεν έχει συντελεστή διεύθυνσης και τα σημεία τομής
και συνεπώς η ζητούμενη ευθεία δεν έχει συντελεστή διεύθυνσης και τα σημεία τομής  (για τη μεγιστοποίηση του εμβαδού του τριγώνου
(για τη μεγιστοποίηση του εμβαδού του τριγώνου  ) προκύπτουν ως τα σημεία τομής της ευθείας
) προκύπτουν ως τα σημεία τομής της ευθείας  με την έλλειψη.
με την έλλειψη. Μπορούμε εύκολα να αποδείξουμε ότι το μέγιστο θα παρατηρηθεί από την επαφή της διερχόμενης (όταν
 ) από την εστία
) από την εστία  εφαπτόμενης (εφαπτομένων ) στον κύκλο με διάμετρο το μικρό άξονα της έλλειψης αφού εύκολα διαπιστώνεται ότι
εφαπτόμενης (εφαπτομένων ) στον κύκλο με διάμετρο το μικρό άξονα της έλλειψης αφού εύκολα διαπιστώνεται ότι 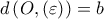
Στάθης
Τι περιμένετε λοιπόν ναρθεί , ποιόν καρτεράτε να σας σώσει.
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
Εσείς οι ίδιοι με τα χέρια σας , με το μυαλό σας με την πράξη αν δεν αλλάξετε τη μοίρα σας ποτέ της δεν θα αλλάξει
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
