 με
με  .
.1) Nα βρεθεί ο τύπος της συνάρτησης
2) Να αποδειχθεί οτι

3) Aν
 μία αρχική της
μία αρχική της  να λυθεί η εξίσωση
να λυθεί η εξίσωση 
4) Nα βρείτε το εμβαδό του χωρίου που περικλείεται απο την γ.π. της συνάρτησης
 , την ασύμπτωτη στο
, την ασύμπτωτη στο  και τον άξονα
και τον άξονα 
5) Αποδείξτε οτι

Συντονιστής: Μπάμπης Στεργίου
 με
με  .
.
 μία αρχική της
μία αρχική της  να λυθεί η εξίσωση
να λυθεί η εξίσωση 
 , την ασύμπτωτη στο
, την ασύμπτωτη στο  και τον άξονα
και τον άξονα 






 (1)
(1)
 (2)
(2)








 για
για 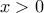
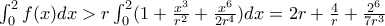
 παίρνει ελάχιστη τιμή στο
παίρνει ελάχιστη τιμή στο 
 για
για η
η 
 έχουμε
έχουμε 
![f,g:[a,b]\rightarrow \mathbb{R} f,g:[a,b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/99edc50ed57090a234ce3ed765509ca7.png) συνεχείς με
συνεχείς με 
 ώστε
ώστε 
![k,l\epsilon [a,b] k,l\epsilon [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/fbb7e9551403beb4a304e2da578d63ce.png) ώστε
ώστε  για
για ![x\epsilon [a,b] x\epsilon [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/081c084383b7679e2d4e389208c19a3b.png)
 και ολοκληρώνοντας παίρνουμε
και ολοκληρώνοντας παίρνουμε (1)
(1)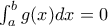 παίρνουμε
παίρνουμε  οποιοδήποτε.
οποιοδήποτε. σταθερή οπότε παίρνουμε
σταθερή οπότε παίρνουμε  οποιοδήποτε.
οποιοδήποτε.




 ασύμπτωτη είναι η ευθεία
ασύμπτωτη είναι η ευθεία 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες