Δίνεται η συνάρτηση
 , η οποία είναι συνεχής στο
, η οποία είναι συνεχής στο  και ισχύει ότι
και ισχύει ότι  .
. Αν γνωρίζουμε ότι
 τότε:
τότε:Α. Υπάρχει
 ώστε
ώστε 
Β. Αν επιπλέον ακόμη ισχύει
•

•

τότε να δείξετε ότι :
i)

ii)

Φιλικά και Μαθηματικά
Βασίλης
Συντονιστής: Μπάμπης Στεργίου
 , η οποία είναι συνεχής στο
, η οποία είναι συνεχής στο  και ισχύει ότι
και ισχύει ότι  .
.  τότε:
τότε: ώστε
ώστε 




Καλημέρα.KAKABASBASILEIOS έγραψε:...Καλησπέραμια αποψινή δημιουργία μάλλον απαιτητική...
Δίνεται η συνάρτηση, η οποία είναι συνεχής στο
και ισχύει ότι
.
Αν γνωρίζουμε ότιτότε:
Α. Υπάρχειώστε
Β. Αν επιπλέον ακόμη ισχύει
•
•
τότε να δείξετε ότι :
i)
ii)
Φιλικά και Μαθηματικά
Βασίλης





![\displaystyle{\Rightarrow \int\limits_{0}^{1}{(3f(x)-2f(1))dx} + \left[2x-2x^2 \right]_0^1 =0} \displaystyle{\Rightarrow \int\limits_{0}^{1}{(3f(x)-2f(1))dx} + \left[2x-2x^2 \right]_0^1 =0}](/forum/ext/geomar/texintegr/latexrender/pictures/c59bd5055c2db3269c1140bdcf9a5fe2.png)



![\displaystyle{\Rightarrow \int\limits_{0}^{1}{\left( f(1)+2x-1\right)dx}=2 \Rightarrow \left[f(1)x+x^2 -x \right]_0^1 =2\Rightarrow \boxed{f(1)=2}} \displaystyle{\Rightarrow \int\limits_{0}^{1}{\left( f(1)+2x-1\right)dx}=2 \Rightarrow \left[f(1)x+x^2 -x \right]_0^1 =2\Rightarrow \boxed{f(1)=2}}](/forum/ext/geomar/texintegr/latexrender/pictures/bdaa32817e324e20a433cec855d8335f.png)

 τότε
τότε  άρα Cauchy και συνεχής
άρα Cauchy και συνεχής  οποτε
οποτε  και ανικαθιστώντας στην σχέση που δίνεται
και ανικαθιστώντας στην σχέση που δίνεται 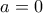
...Καλησπέρα...KAKABASBASILEIOS έγραψε: Δίνεται η συνάρτηση, η οποία είναι συνεχής στο
και ισχύει ότι
.
Αν γνωρίζουμε ότιτότε:
Α. Υπάρχειώστε
Β. Αν επιπλέον ακόμη ισχύει
•
•
τότε να δείξετε ότι :
i)
ii)



 , όπου
, όπου  μια παράγουσα της
μια παράγουσα της  στο
στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ,έγινε ένα ΘΜΤ στο
,έγινε ένα ΘΜΤ στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) για την
για την 
 και
και 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες