Να αποδειχθεί η ανισότητα

για
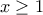 .
.[Όπως υποδηλώνει και ο τίτλος, η ανισότητα είναι δύσκολη μόνον για σχετικά μικρές τιμές του
 . Η λύση μου κάπως περιπετειώδης...]
. Η λύση μου κάπως περιπετειώδης...]Συντονιστής: Μπάμπης Στεργίου

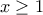 .
. . Η λύση μου κάπως περιπετειώδης...]
. Η λύση μου κάπως περιπετειώδης...]




 , για
, για  .
.Ταχυδακτυλουργική η παρέμβαση σου, αγαπητέ Λάμπρο: δεν καταλαβαίνω πως κατάφερες να καταλήξεις, με σωστά βήματα (και χρήση τηςΛάμπρος Μπαλός έγραψε: ↑Τρί Ιούλ 06, 2021 10:06 amΙσοδύναμα,
Αφού
αρκεί να αποδείξουμε ότι
, για
.
Θα επανέλθω..
Όχι. Ζητώ συγγνώμη. Έκανα δεύτερη φορά το ίδιο αριθμητικό λάθος. Παρόλα αυτά, η παραπάνω σχέση ισχύει, την αφήνω μπας και βοηθήσει κάπου. Θα την ξανακοιτάξω άλλη στιγμή.
 για
για  ) εννοείται, σε λιγότερο σφιχτή (βλ. σχήματα) αλλά πιο δύσκολη*, και πιο όμορφη*, ανισότητα!
) εννοείται, σε λιγότερο σφιχτή (βλ. σχήματα) αλλά πιο δύσκολη*, και πιο όμορφη*, ανισότητα! γυροφέρνει κοντά στην περιοχή του
γυροφέρνει κοντά στην περιοχή του  για μεγάλο σχετικά διάστημα για
για μεγάλο σχετικά διάστημα για  .
.Λάμπρο πιστεύω γενικώς ότι μία ανισότητα είναι ενδιαφέρουσα όταν είναι είτε χρήσιμη είτε όμορφη: στην παρούσα περίπτωση η δική μου αρχική μορφή είναι ενδεχομένως χρήσιμη (για κάτι συγκεκριμένο που δεν έχω αναφέρει ακόμη), η δική σου μορφή είναι όμορφη, κομψότατη.Λάμπρος Μπαλός έγραψε: ↑Παρ Ιούλ 09, 2021 5:19 pmΚαλησπέρα σας κύριε Μπαλόγλου.
Ο σκοπός μου ήταν μόνο να δημιουργήσω μια πιο κομψή εμφάνιση και στη συνέχεια μια κομψή λύση (δεν την έχω βρει). Στάθηκα τυχερός στη χαλάρωση της ανισότητας, δεν παρατήρησα ότι τογυροφέρνει κοντά στην περιοχή του
για μεγάλο σχετικά διάστημα για
.
Παρόλα αυτά, δεν έχω ακόμη λύση. Θα την κοιτάξω αργά το βράδυ.
Έχει ήδη επιλυθεί εδώ μέσω της ιδιαίτερα ενδιαφέρουσας αναγωγής του Λάμπρου (#2), παρουσιάζω όμως παρακάτω και την αρχική μου λύση:
 , οπότε
, οπότε  και
και 
 για
για  και
και  , άρα
, άρα  για
για  . Επειδή ισχύει και η
. Επειδή ισχύει και η  , προκύπτει άμεσα η
, προκύπτει άμεσα η  για
για  . Aρκεί συνεπώς να δειχθεί η
. Aρκεί συνεπώς να δειχθεί η  για
για  .
.  στο
στο  λαμβάνουμε την ανισότητα
λαμβάνουμε την ανισότητα  , από την οποία προκύπτει η
, από την οποία προκύπτει η ![f(x)>(ln2)(x-1)-\dfrac{(x-1)^2}{1+x^2}-\dfrac{(x-1)}{2}=(x-1)\left[ln2-\dfrac{x-1}{1+x^2}-\dfrac{1}{2}\right] f(x)>(ln2)(x-1)-\dfrac{(x-1)^2}{1+x^2}-\dfrac{(x-1)}{2}=(x-1)\left[ln2-\dfrac{x-1}{1+x^2}-\dfrac{1}{2}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/7ce2a454227102ea9ac32a985a1ef431.png) . Αρκεί συνεπώς να δειχθεί η
. Αρκεί συνεπώς να δειχθεί η  για
για  , όπου
, όπου  : αυτό προκύπτει από τις
: αυτό προκύπτει από τις  και
και  για
για  (καθώς
(καθώς  , οπότε
, οπότε  ).
).
![x \in [0,1] x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) ,
,  .
. .
. βλέπουμε ότι
βλέπουμε ότι  , άρα από Θεώρημα Rolle υπάρχει ένα τουλάχιστον σημείο μηδενισμού της
, άρα από Θεώρημα Rolle υπάρχει ένα τουλάχιστον σημείο μηδενισμού της  στο
στο  . Το σημείο αυτό είναι μοναδικό: αν υπήρχαν δύο σημεία μηδενισμού της
. Το σημείο αυτό είναι μοναδικό: αν υπήρχαν δύο σημεία μηδενισμού της  στο
στο  , τότε, επειδή ισχύει επίσης η
, τότε, επειδή ισχύει επίσης η  , θα υπήρχαν δύο σημεία μηδενισμού της
, θα υπήρχαν δύο σημεία μηδενισμού της  , άτοπο. Η μη αρνητικότητα λοιπόν της
, άτοπο. Η μη αρνητικότητα λοιπόν της  σε ολόκληρο το
σε ολόκληρο το  θα προέκυπτε από την ύπαρξη ενός και μόνον σημείου στο
θα προέκυπτε από την ύπαρξη ενός και μόνον σημείου στο  όπου αυτή είναι θετική (καθώς η ύπαρξη αρνητικής τιμής θα σήμαινε και την ύπαρξη αρνητικού τοπικού ελαχίστου). Παρατηρούμε ότι
όπου αυτή είναι θετική (καθώς η ύπαρξη αρνητικής τιμής θα σήμαινε και την ύπαρξη αρνητικού τοπικού ελαχίστου). Παρατηρούμε ότι  για
για  : θέτοντας
: θέτοντας  ισχύουν οι
ισχύουν οι  και
και  , άρα και η
, άρα και η  .
. για
για  και
και  έχουμε
έχουμε  και
και  : από
: από  και
και  λαμβάνουμε
λαμβάνουμε  , και σε συνδυασμό με την
, και σε συνδυασμό με την 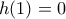 προκύπτει η ζητούμενη
προκύπτει η ζητούμενη  (για
(για  και
και  πάντοτε).
πάντοτε).Ωραίο το τεχνασματάκι με τηνgbaloglou έγραψε: ↑Σάβ Ιούλ 17, 2021 2:10 pmΔύο αποδείξεις για την Α
(Ι) Θέτονταςβλέπουμε ότι
, άρα από Θεώρημα Rolle υπάρχει ένα τουλάχιστον σημείο μηδενισμού της
στο
. Το σημείο αυτό είναι μοναδικό: αν υπήρχαν δύο σημεία μηδενισμού της
στο
, τότε, επειδή ισχύει επίσης η
, θα υπήρχαν δύο σημεία μηδενισμού της
, άτοπο. Η μη αρνητικότητα λοιπόν της
σε ολόκληρο το
θα προέκυπτε από την ύπαρξη ενός και μόνον σημείου στο
όπου αυτή είναι θετική (καθώς η ύπαρξη αρνητικής τιμής θα σήμαινε και την ύπαρξη αρνητικού τοπικού ελαχίστου). Παρατηρούμε ότι
για
: θέτοντας
ισχύουν οι
και
, άρα και η
.
 , που οδηγεί και στην παραλειπόμενη εδώ απόδειξη (ΙΙ), μπορεί όμως και να αποφευχθεί χάριν μιας 'αυτοδύναμης' απόδειξης (Ι): αρκεί να παρατηρηθεί ότι ισχύει η
, που οδηγεί και στην παραλειπόμενη εδώ απόδειξη (ΙΙ), μπορεί όμως και να αποφευχθεί χάριν μιας 'αυτοδύναμης' απόδειξης (Ι): αρκεί να παρατηρηθεί ότι ισχύει η  , οπότε η ύπαρξη σημείων θετικότητας της
, οπότε η ύπαρξη σημείων θετικότητας της  είναι άμεση*. (Πράγματι η ζητούμενη
είναι άμεση*. (Πράγματι η ζητούμενη  είναι ισοδύναμη προς την
είναι ισοδύναμη προς την  για
για  , που προκύπτει εύκολα από τις
, που προκύπτει εύκολα από τις  και
και  .)
.) μπορεί να παραλειφθεί.
μπορεί να παραλειφθεί. αρκεί να χρησιμοποιήσουμε την εύκολη μονοτονία της
αρκεί να χρησιμοποιήσουμε την εύκολη μονοτονία της  (γνησίως φθίνουσα) και την ύπαρξη των σημείων μηδενισμού της
(γνησίως φθίνουσα) και την ύπαρξη των σημείων μηδενισμού της  (
( ) και της
) και της  (
( ).
). αντιτάσσουμε ένα τριώνυμο κατασκευασμένο κατά τέτοιον τρόπο ώστε
αντιτάσσουμε ένα τριώνυμο κατασκευασμένο κατά τέτοιον τρόπο ώστε  ,
,  και
και  .
.Πολύ εύστοχα τα παραπάνω, όταν τα "ξι" έχουν ρόλο στην μελέτη συγκεκριμένων συναρτήσεων τότε είναι ευπρόσδεκτα (θα έλεγα)...Λάμπρος Μπαλός έγραψε: ↑Τρί Ιούλ 20, 2021 1:03 amΗ απόδειξη τουμπορεί να παραλειφθεί.
Στη θεωρούμενη παραπάνωαρκεί να χρησιμοποιήσουμε την εύκολη μονοτονία της
(γνησίως φθίνουσα) και την ύπαρξη των σημείων μηδενισμού της
(
) και της
(
).
Κάπως έτσι κατασκευάστηκε η ανισότητα.
Απέναντι στην κυρτήαντιτάσσουμε ένα τριώνυμο κατασκευασμένο κατά τέτοιον τρόπο ώστε
,
και
.
Σε μικρά διαστήματα, πράγματι επιτυγχάνεται μία σφιχτή ανισότητα. Παρόλα αυτά, δεν ήταν αυτό το ζητούμενο.
Καταδεικνύεται η αξία των υπαρξιακών Θεωρημάτων (εν προκειμένω του Rolle) στη μελέτη μονοτονίας και προσήμου μιας συνάρτησης. Το λέω διότι παρατηρώ ακόμη και τώρα μία γενική αποστροφή προς τα "ξι", βάσιμη μεν (είχε παραγίνει το κακό) αλλά και αρκετά άκριτη πολλές φορές.
 :
: τέτοιο ώστε να ισχύουν, μαζί με την
τέτοιο ώστε να ισχύουν, μαζί με την  , είτε οι
, είτε οι  &
&  είτε οι
είτε οι  &
&  , δηλαδή είτε οι
, δηλαδή είτε οι  &
&  είτε οι
είτε οι  &
&  . Από την
. Από την  προκύπτουν οι
προκύπτουν οι  και
και  . Οι
. Οι  &
&  δίνουν
δίνουν  και
και  , οπότε σε συνδυασμό με την
, οπότε σε συνδυασμό με την  λαμβάνουμε
λαμβάνουμε  , ανισότητα που ισχύει για
, ανισότητα που ισχύει για  : καταλήγουμε στην
: καταλήγουμε στην  . (Παραλείπω τις λεπτομερειες, αλλά η αντίθετη περίπτωση είναι αδύνατη, καθώς οι
. (Παραλείπω τις λεπτομερειες, αλλά η αντίθετη περίπτωση είναι αδύνατη, καθώς οι  &
&  οδηγούν στην αντίστροφη και μη ισχύουσα ανισότητα
οδηγούν στην αντίστροφη και μη ισχύουσα ανισότητα  .)
.) [Βελτιώνει κάπως την ανισότητα Β, υπάρχουν και άλλα περιθώρια βελτίωσης]
[Βελτιώνει κάπως την ανισότητα Β, υπάρχουν και άλλα περιθώρια βελτίωσης] για
για  ['Οριακή' ανισότητα, προτείνεται ανεξάρτητα εδώ]
['Οριακή' ανισότητα, προτείνεται ανεξάρτητα εδώ]Η απάντηση που είχα στο μυαλό μου για το Β, ήθελε να βάζουμε όπουΛάμπρος Μπαλός έγραψε: ↑Τρί Ιούλ 13, 2021 10:56 pm
Α. Να αποδείξετε ότι
για,
.
Β. Να αποδείξετε ότι
.
 , για
, για ![x \in (0,1] x \in (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5f3bd0dafa13199e5ec59664dccbce7e.png) , οπότε
, οπότε , για
, για ![x \in [0,1] x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) .
.To (ii) το συζητήσαμε (εδώ), για το (i) έχω να πω τα εξής:
 για
για  .
.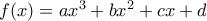 τέτοια ώστε
τέτοια ώστε  ,
,  KAI
KAI  όταν
όταν  : προκύπτουν οι
: προκύπτουν οι  ,
,  , και, από αντικατάσταση,
, και, από αντικατάσταση,  ^ μία στρατηγική για πιο σφικτή ανισότητα είναι, λόγω
^ μία στρατηγική για πιο σφικτή ανισότητα είναι, λόγω  , να μηδενιστούν οι χαμηλότεροι όροι μέσω
, να μηδενιστούν οι χαμηλότεροι όροι μέσω 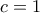 και
και  , οπότε
, οπότε  : ΔΕΝ εξασφαλίζεται έτσι η επιζητούμενη θετικότητα (λόγω
: ΔΕΝ εξασφαλίζεται έτσι η επιζητούμενη θετικότητα (λόγω  ), εξακολουθεί όμως να ισχύει η προκύπτουσα ανισότητα (αμέσως παρακάτω) ... που προτείνεται ανεξάρτητα εδώ.
), εξακολουθεί όμως να ισχύει η προκύπτουσα ανισότητα (αμέσως παρακάτω) ... που προτείνεται ανεξάρτητα εδώ.  προκύπτει η
προκύπτει η
 ) και από αυτό που εσφαλμένα υποσχέθηκα (
) και από αυτό που εσφαλμένα υποσχέθηκα ( ) και, ελάχιστα, από αυτό του Λάμπρου (
) και, ελάχιστα, από αυτό του Λάμπρου ( ). [Ακριβής τιμή ολοκληρώματος
). [Ακριβής τιμή ολοκληρώματος  .]
.]Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες