 , του ορθογωνίου τριγώνου
, του ορθογωνίου τριγώνου  ,
,κατά τμήματα :
 . Βρείτε την μέγιστη τιμή του λόγου :
. Βρείτε την μέγιστη τιμή του λόγου :  ,
,καθώς και το όριο αυτού του λόγου , όταν :
 .
.Συντονιστής: Καρδαμίτσης Σπύρος
 , του ορθογωνίου τριγώνου
, του ορθογωνίου τριγώνου  ,
, . Βρείτε την μέγιστη τιμή του λόγου :
. Βρείτε την μέγιστη τιμή του λόγου :  ,
, .
. και
και  .
.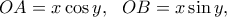 οπότε
οπότε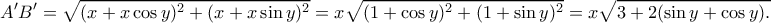



 είναι
είναι 

 κέντρων
κέντρων  που τέμνονται στο
που τέμνονται στο  .
.
 ( βαίνουν στο ίδιο τόξο του μεγάλου ημικυκλίου) και
( βαίνουν στο ίδιο τόξο του μεγάλου ημικυκλίου) και  ( βαίνουν στο ίδιο τόξο του μικρού ημικυκλίου )
( βαίνουν στο ίδιο τόξο του μικρού ημικυκλίου ) έχουν
έχουν  ( παραπληρώματα ίσων γωνιών ) , άρα είναι ίσα . Άμεσες συνέπειες :
( παραπληρώματα ίσων γωνιών ) , άρα είναι ίσα . Άμεσες συνέπειες : είναι ισοσκελή ορθογώνια . Ο λόγος του οποίου ζητώ το μέγιστο ισούται με το λόγο:
είναι ισοσκελή ορθογώνια . Ο λόγος του οποίου ζητώ το μέγιστο ισούται με το λόγο:  .
.  είναι κάθετη στο μέσο
είναι κάθετη στο μέσο  της χορδής
της χορδής  .
. 
 συμπέσουν.
συμπέσουν.
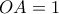 θα είναι
θα είναι 
 το τρίγωνο
το τρίγωνο  θα έχει
θα έχει  (=έστω
(=έστω  ) και άρα
) και άρα  που είναι και ο ζητούμενος λόγος.
που είναι και ο ζητούμενος λόγος.
 πλησιάζει στο
πλησιάζει στο  ( όπως ακριβώς προβλέπει η εκφώνηση) με τo
( όπως ακριβώς προβλέπει η εκφώνηση) με τo  να μένει σταθερό ή ν απομακρύνεται από το
να μένει σταθερό ή ν απομακρύνεται από το  .
. και
και  , παίρνουμε για τον ζητούμενο λόγο την συνάρτηση :
, παίρνουμε για τον ζητούμενο λόγο την συνάρτηση : , η οποία είναι ουσιαστικά αυτή του ( προεορτάζοντος ) Θάνου ( με την ίδια συνέχεια ) .
, η οποία είναι ουσιαστικά αυτή του ( προεορτάζοντος ) Θάνου ( με την ίδια συνέχεια ) .Με καλή επιλογή των μεταβλητών μπορούμε να γλυτώσουμε πολύ κόπο. Για παράδειγμα, με βάση το σχήμα του Θανάση, αντί για
 σταθερό, να πάρουμε
σταθερό, να πάρουμε  και
και  . Σε αυτή την περίπτωση, αντί να πάρουμε
. Σε αυτή την περίπτωση, αντί να πάρουμε  , εξετάζουμε το
, εξετάζουμε το  .
.  (είναι βέβαια
(είναι βέβαια  ) αλλά θα δούμε ότι δεν χρειάζεται να το κουβαλάμε πλήρες. Απλά στο όριο
) αλλά θα δούμε ότι δεν χρειάζεται να το κουβαλάμε πλήρες. Απλά στο όριο  που θα πάρουμε στο τέλος, έχουμε
που θα πάρουμε στο τέλος, έχουμε  .
. 
 , και λοιπά.
, και λοιπά.  , έχουμε
, έχουμε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες