exdx έγραψε: ↑Δευ Αύγ 17, 2020 4:27 pm
Δίνονται οι πραγματικοί αριθμοί

, με

και η συνάρτηση

Α) Να βρείτε τους

ώστε η

να είναι συνεχής στο

Β) Για τις τιμές των

που βρήκατε στο (Α) :
α) Να δείξετε ότι

για κάθε

.
β) Να βρείτε την παράγωγο της

για κάθε

.
γ) Να δείξετε ότι η

είναι γνησίως αύξουσα στο πεδίο ορισμού της .
δ) Να δείξετε ότι είναι κοίλη στο πεδίο ορισμού της .
ε) Να υπολογίσετε το εμβαδόν

του χωρίου που περικλείεται από τη γραφική παράσταση της

, τον

και τις ευθείες με εξισώσεις

, όπου

και κατόπιν το

...γειά σου Γιώργη...μια αντιμετώπιση....
ΛΥΣΗ
Α) Επειδή η

είναι συνεχής στο
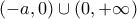
για να είναι συνεχής στο

αναγκαία συνεχής και
στο

δηλαδή πρέπει και αρκεί

(1)
Είναι τώρα

οπότε

και επειδή

αναγκαία λόγω της ισότητας

τότε
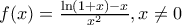
και


έτσι

Β) Είναι τώρα

α) Ως γνωστόν ισχύει

ή

ή

και η ισότητα μόνο για

επομένως προφανώς ισχύει ότι

για κάθε

.
β) Είναι για

παραγωγίσιμη με



Στο

έχουμε

με

επομένως

γ) Για την συνάρτηση

είναι

και

(όπως προηγούμενα για

άρα για

άρα

και για

άρα

έτσι είναι

επομένως

είναι γνησίως αύξουσα στο πεδίο ορισμού της.
δ) Είναι τώρα

οπότε

(2)
Τώρα για την συνάρτηση
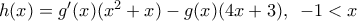
είναι

και


(3)

(4)

(5) και

(6)
Τώρα λόγω (4),(5),(6) η (3) γίνεται

και σύμφωνα με προηγούμενα είναι για
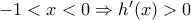
άρα η

είναι
γνήσια αύξουσα στο
![(-1,\,0] (-1,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/22d84ed8c88a3d8b57aae483dfc11b55.png)
και

άρα η

είναι γνήσια φθίνουσα στο

άρα έχουμε μέγιστο στο

το

και επομένως

άρα η
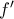
γνήσια φθίνουσα και επομένως η

κοίλη.
ε) Το ζητούμενο εμβαδό είναι


![=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}-\int\limits_{k}^{1}{\frac{1}{x}}(\frac{1}{x+1}-1)dx=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\int\limits_{k}^{1}{\frac{1}{x+1}}dx= =\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}-\int\limits_{k}^{1}{\frac{1}{x}}(\frac{1}{x+1}-1)dx=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\int\limits_{k}^{1}{\frac{1}{x+1}}dx=](/forum/ext/geomar/texintegr/latexrender/pictures/f9c7fe45e4f31bf74e3c1344970fefb3.png)
![=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\left[ \ln (x+1) \right]_{k}^{1}=2\ln 2-\ln (k+1)-\frac{\ln (k+1)}{k} =\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\left[ \ln (x+1) \right]_{k}^{1}=2\ln 2-\ln (k+1)-\frac{\ln (k+1)}{k}](/forum/ext/geomar/texintegr/latexrender/pictures/d05956a58ae6440d08d892896df66556.png)
και εύκολα

...ελπίζω να μην εχω κάνει πατάτα στις πράξεις...
Φιλικά και Μαθηματικά
Βασίλης
 , με
, με  και η συνάρτηση
και η συνάρτηση 
 ώστε η
ώστε η  να είναι συνεχής στο
να είναι συνεχής στο 
 που βρήκατε στο (Α) :
που βρήκατε στο (Α) : για κάθε
για κάθε  .
. για κάθε
για κάθε  .
. είναι γνησίως αύξουσα στο πεδίο ορισμού της .
είναι γνησίως αύξουσα στο πεδίο ορισμού της . του χωρίου που περικλείεται από τη γραφική παράσταση της
του χωρίου που περικλείεται από τη γραφική παράσταση της  , τον
, τον  και τις ευθείες με εξισώσεις
και τις ευθείες με εξισώσεις  , όπου
, όπου  και κατόπιν το
και κατόπιν το 

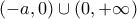 για να είναι συνεχής στο
για να είναι συνεχής στο  δηλαδή πρέπει και αρκεί
δηλαδή πρέπει και αρκεί  (1)
(1) οπότε
οπότε  και επειδή
και επειδή 

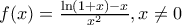 και
και 
 έτσι
έτσι 

 ή
ή  ή
ή  και η ισότητα μόνο για
και η ισότητα μόνο για 
 παραγωγίσιμη με
παραγωγίσιμη με 


 με
με 

 είναι
είναι  και
και  (όπως προηγούμενα για
(όπως προηγούμενα για  άρα
άρα  και για
και για  άρα
άρα  έτσι είναι
έτσι είναι 
 οπότε
οπότε  (2)
(2)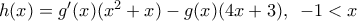 είναι
είναι  και
και 
 (3)
(3) (4)
(4) (5) και
(5) και (6)
(6) και σύμφωνα με προηγούμενα είναι για
και σύμφωνα με προηγούμενα είναι για 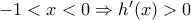 άρα η
άρα η  είναι
είναι ![(-1,\,0] (-1,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/22d84ed8c88a3d8b57aae483dfc11b55.png) και
και  άρα η
άρα η  άρα έχουμε μέγιστο στο
άρα έχουμε μέγιστο στο  άρα η
άρα η 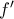 γνήσια φθίνουσα και επομένως η
γνήσια φθίνουσα και επομένως η  κοίλη.
κοίλη.

![=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}-\int\limits_{k}^{1}{\frac{1}{x}}(\frac{1}{x+1}-1)dx=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\int\limits_{k}^{1}{\frac{1}{x+1}}dx= =\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}-\int\limits_{k}^{1}{\frac{1}{x}}(\frac{1}{x+1}-1)dx=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\int\limits_{k}^{1}{\frac{1}{x+1}}dx=](/forum/ext/geomar/texintegr/latexrender/pictures/f9c7fe45e4f31bf74e3c1344970fefb3.png)
![=\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\left[ \ln (x+1) \right]_{k}^{1}=2\ln 2-\ln (k+1)-\frac{\ln (k+1)}{k} =\left[ \frac{\ln (x+1)-x}{x} \right]_{k}^{1}+\left[ \ln (x+1) \right]_{k}^{1}=2\ln 2-\ln (k+1)-\frac{\ln (k+1)}{k}](/forum/ext/geomar/texintegr/latexrender/pictures/d05956a58ae6440d08d892896df66556.png) και εύκολα
και εύκολα 