 με
με 
α) Να μελετηθεί ως προς τη μονοτονία και τα ακρότατα
β) Να μελετηθεί ως προς την κυρτότητα και τα σημεία καμπής
γ) Να βρείτε τις ασύμπτωτες της
 και να σχεδιάσετε τη
και να σχεδιάσετε τη  .
.δ) Θεωρούμε τον περιορισμό
 της
της  στο
στο  . Να δείξετε ότι η
. Να δείξετε ότι η  αντιστρέφεται και να βρείτε την αντίστροφη .
αντιστρέφεται και να βρείτε την αντίστροφη .ε) Σχεδιάστε τη γραφική παράσταση της
 .
.ζ) Έστω το σημείο
 .
.i) Να βρείτε ποιο σημείο της
 βρίσκεται πλησιέστερα στο
βρίσκεται πλησιέστερα στο  .
.ii) Να αποδείξετε ότι η ευθεία με εξίσωση
 , με
, με  , τέμνει τη
, τέμνει τη  σε δυο σημεία
σε δυο σημεία 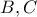 και κατόπιν να βρείτε το
και κατόπιν να βρείτε το  ώστε το εμβαδόν του τριγώνου
ώστε το εμβαδόν του τριγώνου  να είναι το μέγιστο δυνατό .
να είναι το μέγιστο δυνατό .η) Να αποδείξετε ότι
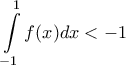


 είναι γνωστή από το μάθημα Πιθανοτήτων ως κατανομή Cauchy, η οποία δεν έχει δεν έχει μέση τιμή και τυπική απόκλιση, αλλά μοιάζει στο σχήμα με την Κανονική Κατανομή (με πιο ψηλές ουρές).
είναι γνωστή από το μάθημα Πιθανοτήτων ως κατανομή Cauchy, η οποία δεν έχει δεν έχει μέση τιμή και τυπική απόκλιση, αλλά μοιάζει στο σχήμα με την Κανονική Κατανομή (με πιο ψηλές ουρές). και
και  .
.![\displaystyle (-\infty ,0] \displaystyle (-\infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/1c62f453a8c0e5da32a5a4ec3e6d61b2.png) και γν αύξουσα στο
και γν αύξουσα στο 
 και
και 
 . Άρα είναι κυρτή στο
. Άρα είναι κυρτή στο ![\displaystyle \left[ -\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right] \displaystyle \left[ -\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/60cdc81e81747e5c4ee7831a84c01516.png) και κοίλη αλλού .
και κοίλη αλλού . άρα η
άρα η  είναι οριζόντια ασύμπτωτη . Κατακόρυφες δεν έχει αφού είναι συνεχής .
είναι οριζόντια ασύμπτωτη . Κατακόρυφες δεν έχει αφού είναι συνεχής . είναι γνησίως αύξουσα , άρα
είναι γνησίως αύξουσα , άρα  , άρα αντιστρέφεται .
, άρα αντιστρέφεται .
 απέχει από το
απέχει από το 


 έχει ελάχιστο για
έχει ελάχιστο για 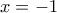 και για
και για 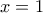 ίσο με
ίσο με 
 , τέμνει τη
, τέμνει τη 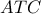 όπου το
όπου το  είναι στον
είναι στον  .
.

 , οπότε
, οπότε 
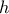 έχει μέγιστο για
έχει μέγιστο για  ίσο με
ίσο με  .Τότε το μέγιστο εμβαδόν του
.Τότε το μέγιστο εμβαδόν του  .
.![\displaystyle [0,1] \displaystyle [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3c768608c76c88b7847dbf1ec30ec3d4.png) ισχύει :
ισχύει : 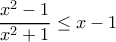
![\displaystyle \int_{0}^{1}{\left( \frac{{{x}^{2}}-1}{{{x}^{2}}+1} \right)}dx<\int_{0}^{1}{(x-1})dx=\left[ \frac{{{x}^{2}}}{2}-x \right]_{0}^{1}=-\frac{1}{2} \displaystyle \int_{0}^{1}{\left( \frac{{{x}^{2}}-1}{{{x}^{2}}+1} \right)}dx<\int_{0}^{1}{(x-1})dx=\left[ \frac{{{x}^{2}}}{2}-x \right]_{0}^{1}=-\frac{1}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/f7bf9c35cbe0a170a4cd46a9d2012451.png)
