KARKAR έγραψε: ↑Παρ Μάιος 22, 2020 8:14 pm
Με προαιρετικό ερώτημα.pngΔίνεται η συνάρτηση :

.
Α) Για ποιες τιμές του

, η

έχει πεδίο ορισμού ολόκληρο το

;
Β) Για ποια τιμή του

, η

έχει σύνολο τιμών το :

;
Γ) Για το

που βρήκατε , βρείτε την εφαπτομένη της

με την μέγιστη κλίση .
Δ) ( Προαιρετικό ) Για το ίδιο

, βρείτε τον μέγιστο κύκλο , ο οποίος έχει με την

μοναδικό κοινό σημείο , το σημείο που αυτή εφάπτεται στον οριζόντιο άξονα .
Γράφω τα
A,B,Δ.
A) Πρέπει για κάθε

να ισχύει

που εύκολα βλέπουμε βρίσκοντας τη
διακρίνουσα ότι

B) θέλουμε να υπάρχει

στο πεδίο ορισμού της συνάρτησης τέτοιο, ώστε

και επιπλέον
για κάθε

στο πεδίο ορισμού να ικανοποιείται η

. Το τριώνυμο

έχει
ελάχιστο το

και αφού θέλουμε να παίρνει την τιμή

αναγκαστικά θα
πρέπει να ισχύει

H δεύτερη, όμοια, μας δίνει

. Τελικά βρίσκουμε ότι

το οποίο εύκολα επαληθεύουμε ότι μας δίνει
το ζητούμενο, δηλαδή σύνολο τιμών το

. Συγκεκριμένα θα έχουμε τότε

και

. H συνέχεια της

συμπληρώνει την απόδειξη.
Δ) Ο μέγιστος εφαπτόμενος κύκλος θα έχει ακτίνα

(ακτίνα καμπυλότητας) και κέντρο το

 .
. , η
, η  έχει πεδίο ορισμού ολόκληρο το
έχει πεδίο ορισμού ολόκληρο το  ;
; , η
, η  έχει σύνολο τιμών το :
έχει σύνολο τιμών το :  ;
; που βρήκατε , βρείτε την εφαπτομένη της
που βρήκατε , βρείτε την εφαπτομένη της  με την μέγιστη κλίση .
με την μέγιστη κλίση . , βρείτε τον μέγιστο κύκλο , ο οποίος έχει με την
, βρείτε τον μέγιστο κύκλο , ο οποίος έχει με την 

 να ισχύει
να ισχύει  που εύκολα βλέπουμε βρίσκοντας τη
που εύκολα βλέπουμε βρίσκοντας τη 
 στο πεδίο ορισμού της συνάρτησης τέτοιο, ώστε
στο πεδίο ορισμού της συνάρτησης τέτοιο, ώστε  και επιπλέον
και επιπλέον  στο πεδίο ορισμού να ικανοποιείται η
στο πεδίο ορισμού να ικανοποιείται η  . Το τριώνυμο
. Το τριώνυμο  έχει
έχει  και αφού θέλουμε να παίρνει την τιμή
και αφού θέλουμε να παίρνει την τιμή  αναγκαστικά θα
αναγκαστικά θα  H δεύτερη, όμοια, μας δίνει
H δεύτερη, όμοια, μας δίνει  . Τελικά βρίσκουμε ότι
. Τελικά βρίσκουμε ότι  το οποίο εύκολα επαληθεύουμε ότι μας δίνει
το οποίο εύκολα επαληθεύουμε ότι μας δίνει  και
και  . H συνέχεια της
. H συνέχεια της 

 και
και  . Το ζητούμενο είναι να βρεθεί η μέγιστη τιμή της
. Το ζητούμενο είναι να βρεθεί η μέγιστη τιμή της 

 όταν
όταν  . Έστω
. Έστω  ώστε
ώστε  για κάθε
για κάθε  ώστε
ώστε  . Έχουμε τώρα
. Έχουμε τώρα  για κάθε
για κάθε  και
και ![\Delta\leq 0\iff 16-16\,k^2\leq 0\iff k\in\left(-\infty,-1\right]\cup\left[1,+\infty\right) \Delta\leq 0\iff 16-16\,k^2\leq 0\iff k\in\left(-\infty,-1\right]\cup\left[1,+\infty\right)](/forum/ext/geomar/texintegr/latexrender/pictures/da84dcbba06d94490586c3c677bc450e.png) . Τελικά,
. Τελικά, 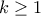 και
και  .
. (που ισχύει για κάθε
(που ισχύει για κάθε  ).
). (
( ) και η ζητούμενη εφαπτομένη είναι αυτή στο σημείο
) και η ζητούμενη εφαπτομένη είναι αυτή στο σημείο 

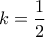 , οπότε έχουμε :
, οπότε έχουμε :  .
. και
και  .
. .
.

 γνησίως φθίνουσα στο
γνησίως φθίνουσα στο ![\left ( -\infty ,-\frac{3}{2} \right ] \left ( -\infty ,-\frac{3}{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/54d60bcdfe69894b9a1e21a4f10b51f5.png)
![f'\left ( \left ( -\infty ,-\frac{3}{2} \right ] \right ) =\left [-1 , 0 \right ) f'\left ( \left ( -\infty ,-\frac{3}{2} \right ] \right ) =\left [-1 , 0 \right )](/forum/ext/geomar/texintegr/latexrender/pictures/3bd78b2a11689d79daf382ca7348da3e.png) .
.
![\left [ -\frac{3}{2} ,\frac{1}{2} \right ] \left [ -\frac{3}{2} ,\frac{1}{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/cff2901abbc231c60ea96a2b02f0ad40.png)
![f'\left ( \left [ -\frac{3}{2} ,\frac{1}{2} \right ] \right ) =\left [-1 , 1 \right ] f'\left ( \left [ -\frac{3}{2} ,\frac{1}{2} \right ] \right ) =\left [-1 , 1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/27fc81b5ac405eeea78df1f95a500a39.png) .
.

 .
. έχει σύνολο τιμών το
έχει σύνολο τιμών το ![[-1,1}] [-1,1}]](/forum/ext/geomar/texintegr/latexrender/pictures/1d4b62d0a50fd9721f15eaa6b5db18be.png) και παρουσιάζει στο
και παρουσιάζει στο 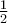 μέγιστο, το
μέγιστο, το  .
. έχουμε την ζητούμενη εφαπτομένη :
έχουμε την ζητούμενη εφαπτομένη : 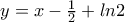 .
.