Προσομοίωσης

Λάμπρος Κατσάπας · #1

Στον παρακάτω σύνδεσμο θα βρείτε ένα διαγώνισμα προσομοίωσης Πανελλαδικών.

https://www.esos.gr/arthra/62583/2o-pro ... Ju4ZdHLxpA

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #2

Γράφω το θέμα Δ ώστε να λυθεί.
(αργότερα ίσως γράψω και τα άλλα)
ΘΕΜΑ Δ
Δίνεται ότι η συνάρτηση $f(x)=a\ln x-(x-2)^{2},x> 0,a\in \mathbb{R}$
παρουσιάζει ακρότατο στο σημείο $x_{0}=1+\sqrt{\frac{3}{2}}$
Να αποδείξετε ότι :

Δ1
a=1

και

κοίλη στο $\Delta =(0,\infty )$

Δ2
η εξίσωση f(x)=0

έχει ακριβώς δύο ρίζες στο $\Delta$

Δ3
$f(x)\leq 3x-4$ για κάθε $x\in \Delta$

Δ4
$\int_{1}^{2}f(x)\sin x dx< 1$

(6+9+5+5)

#3

Πιστεύω ότι το Δ4 πρέπει να διορθωθεί στο $\displaystyle{\int_{4/3}^{2}{f(x)sinxdx}<32/27}$

apotin · #4

ή $\displaystyle{\int_{1}^{2}{f(x)sinxdx}<37/27}$

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

Λάμπρος Κατσάπας · #5

Το ερώτημα είναι εντάξει. Δέχεται τουλάχιστον δύο λύσεις. Δεν μπορώ να γράψω λεπτομέριες τώρα γιατί είμαι από κινητό. Μια περιγραφή μόνο. Η συνάρτηση είναι μικρότερη απο την λογαριθμική η οποιά ειναι μικρότερη από 1 στο διάστημα ολοκλήρωσης. Αν την πολλαπλασιάσουμε με ημιτονο αυτή είναι μικρότερη απο την λογαριθμική επί ημίτονο που είναι μικρότερη από την λογαριθμική που είναι μικρότερη από 1 στο διάστημα ολοκλήρωσης. Αλλιώς, αρκεί να παρατηρήσουμε ότι η συναρτησή μας έχει μοναδική ρίζα μεταξύ των αριθμών 1 και 2 και είναι αρνητική αριστερά της ρίζας και θετική δεξιά μεχρι το 2 (η άλλη είναι μεταξύ 2 και 4, και η επαλήθευση ειναι εύκολη). Άρα το ολοκλήρωμα από 1ως 2 είναι μικρότερο από το ολοκλήρωμα από τη ρίζα μέχρι το 2 που ειναι μικρότερο απο το ολοκλήρωμα της γραμμικής του προηγούμενου ερωτήματος επί ημίτονο που με τη σειρά του είναι μικρότερο από το ολοκλήρωμα της γραμμικήςτο οποίο ειναι τριώνυμο ως προς τη ρίζα. Το τριώνυμο όμως έχει μέγιστο μικρότερο από 1 στο διάστημα μεταξύ 1 και 2.

Christos.N · #6

$0\leq sinx \leq 1,x\in[1,2]$ και λόγω της μονοτονίας της

$1\leq f(x)\leq2 \Rightarrow f(1)\leq f(x)\leq f(2) \Rightarrow -1\leq f(x) \leq ln2 \Rightarrow |f(x)| \leq1$

Απο τις παραπάνω : $|f(x)sinx| \leq 1 \Rightarrow -1 \leq f(x)sinx \leq 1$ .

Απο την τελευταία (αφου δεν είναι παντού η f(x)sinx=1

) το ζητούμενο.

Υστερόγραφο : Η πραγματική του τιμή κατά προσέγγιση είναι η παρακάτω :
$In[4]:= NIntegrate[(f(x)Sin[x],\{x,1,2\}]$
Out[4]= 0.06

μένει να την φτάσουμε σχολικά.

apotin · #7

πολύ καλή Χρήστο

Tolaso J Kos · #8

ΘΕΜΑ Δ

Δίνεται ότι η συνάρτηση $f(x)=a\ln x-(x-2)^{2},x> 0,a\in \mathbb{R}$
παρουσιάζει ακρότατο στο σημείο $x_{0}=1+\sqrt{\frac{3}{2}}$
Να αποδείξετε ότι :

Δ1
και κοίλη στο $\Delta =(0,\infty )$

Δ2
η εξίσωση έχει ακριβώς δύο ρίζες στο $\Delta$

Δ3
$f(x)\leq 3x-4$ για κάθε $x\in \Delta$

Δ4
$\int_{1}^{2}f(x)\sin x dx< 1$

(Δ1) H

είναι παραγωγίσιμη στο $\mathbb{R}$ ως πράξεις παραγωγίσιμων με παράγωγο $\displaystyle{f'(x)=\frac{a}{x} - 2(x-2)}$ . Εφόσον η

παρουσιάζει ακρότατο στο $x_0=1+\sqrt{\frac{3}{2}}$ είναι

$\displaystyle{\begin{aligned} f'(x_0) = 0 &\Leftrightarrow f' \left ( 1+\sqrt{\frac{3}{2}} \right ) =0 \\ &\Leftrightarrow \frac{a}{1+\sqrt{\frac{3}{2}}} - 2\left ( 1+\sqrt{\frac{3}{2}}-2 \right ) =0 \\ &\Leftrightarrow \frac{a}{1+\sqrt{\frac{3}{2}}} = 2 \left ( \sqrt{\frac{3}{2}}-1 \right ) \\ &\Leftrightarrow a = 2 \left ( \sqrt{\frac{3}{2}}-1 \right ) \left ( \sqrt{\frac{3}{2}}+1 \right ) \\ &\Leftrightarrow a = 2 \cdot \frac{1}{2} \\ &\Leftrightarrow a =1 \end{aligned}}$
Η

είναι είναι δύο φορές παραγωγίσιμη με δεύτερη παράγωγο $\displaystyle{f''(x) = -\frac{1}{x^2}-2<0}$ για κάθε x>0

. Άρα είναι κοίλη.

(Δ2) Είναι $f'(x)=\frac{1}{x}-2(x-2)$ . Συνεπώς,

$\displaystyle{\begin{aligned} f'(x) \geq 0 &\Leftrightarrow \frac{1}{x} - 2 \left ( x-2 \right ) \geq 0 \\ &\Leftrightarrow 0 < x \leq 1+ \sqrt{\frac{3}{2}} \end{aligned}}$
Άρα στο $\Delta_1= \left ( 0, 1+ \sqrt{\frac{3}{2}} \right ]$ είναι η

γνήσια αύξουσα ενώ στο $\Delta_2 = \left [1+ \sqrt{\frac{3}{2}} , +\infty \right )$ είναι η

φθίνουσα. Επιπλέον είναι:

$\displaystyle{\lim_{x\rightarrow 0^+} f(x) = \lim_{x\rightarrow 0^+} \left ( \ln x -\left ( x-2 \right )^2 \right ) = -\infty}$
$\displaystyle{\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \left ( \ln x -\left ( x-2 \right )^2 \right )= \lim_{x\rightarrow +\infty} \left ( x-2 \right )^2 \left ( \frac{\ln x}{\left ( x-2 \right )^2} - 1 \right) =-\infty}$

Επιπλέον $\displaystyle{f\left ( 1+\sqrt{\frac{3}{2}} \right ) = \ln \left ( 1+\sqrt{\frac{3}{2}} \right ) +\sqrt{6} - \frac{5}{2}}$ . Η

είναι γνήσια αύξουσα και συνεχής στο $\left(0, 1+ \sqrt{\frac{3}{2}} \right]$ και επειδή το $0 \in f(\Delta_1)$ έπεται ότι η εξίσωση f(x)=0

έχει ρίζα στο $\Delta_1$ . Όμοια στο $\Delta_2$ .

(Δ3) Η εφαπτομένη στο

( προφανής τιμή ή λύνοντας την εξίσωση f'(x)=3

) είναι η ευθεία y=3x-4

και επειδή η

είναι κοίλη το ζητούμενο έπεται $f(x) \leq 3x-4$ .

(Δ4) Είναι $0\leq \sin x \leq 1$ για κάθε $x\in[1,2]$ και λόγω της μονοτονίας της

είναι

$\displaystyle{1\leq f(x)\leq 2 < 1+\sqrt{\frac{3}{2}} \Rightarrow f(1)\leq f(x)\leq f(2) \Rightarrow -1\leq f(x) \leq \ln 2 ^{(*)} \Rightarrow |f(x)| \leq1}$
Από τις παραπάνω βγάζουμε ότι $|f(x) \sin x| \leq 1 \Rightarrow -1 \leq f(x) \sin x \leq 1$ . Από την τελευταία (αφού δεν είναι παντού η $f(x)\sin x=1$ ) το ζητούμενο έπεται:

$\displaystyle{\int_{1}^{2} f(x) \sin x \, \mathrm{d}x < \int_{1}^{2}\, \mathrm{d}x =1}$ (*)

$\ln x \leq x -1 \Rightarrow \ln 2 <2-1=1$

#9

Για να εχει σχεση με τα προηγούμενα to Δ4 (Δεν είναι υποχρεωτικό αλλά μια και προκειται για διαγωνισμα...)

1.Από Fermat $\displaystyle{f'(x_0)=0...a=1}$ ακόμη $\displaystyle{f''(x)=-\frac{1}{x^2}-2<0}$ f κοίλη για $\displaystyle{x>0}$

2. $\displaystyle{f(1)<0,f(2)>0,f(4)=ln4-4<0}$ αφού $\displaystyle{lnx<x-1<x}$ Mε 2 ΘΒ έχουμε τουλάχιστον 2 λύσεις και από τον πινακα μονοτονίας βλέπουμε... οτι είναι μοναδικές (υπάρχουν και άλλοι τρόποι οπως πχ δεν μπορεί σε μια κοιλη συνάρτηση να υπάρχουν 3 συνευθειακά σημεία)

3.παρατηρουμε ότι η $\displaystyle{y=3x-4}$ είναι η εφαπτομένη της $\displaystyle{f}$ στο $\displaystyle{1}$ και αφού η $\displaystyle{f}$ είναι κοίλη Η ανίσωση είναι αληθής (f κατω από την εφαπτομένη της)

4. Στο $\displaystyle{[4/3,2]}$ είναι $\displaystyle{Sinx<x}$ και λόγω του 3. έχουμε $\displaystyle{\int_{4/3}^{2}{f(x)sinxdx}<\int_{4/3}^{2}{(3x^2-4x)dx}=32/27}$

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #10

Christos.N έγραψε: ↑
Κυρ Μάιος 12, 2019 8:07 pm
$0\leq sinx \leq 1,x\in[1,2]$ και λόγω της μονοτονίας της

$1\leq f(x)\leq2 \Rightarrow f(1)\leq f(x)\leq f(2) \Rightarrow -1\leq f(x) \leq ln2 \Rightarrow |f(x)| \leq1$

Απο τις παραπάνω : $|f(x)sinx| \leq 1 \Rightarrow -1 \leq f(x)sinx \leq 1$ .

Απο την τελευταία (αφου δεν είναι παντού η ) το ζητούμενο.

Υστερόγραφο : Η πραγματική του τιμή κατά προσέγγιση είναι η παρακάτω :
$In[4]:= NIntegrate[(f(x)Sin[x],\{x,1,2\}]$

μένει να την φτάσουμε σχολικά.

Κατά αρχάς να σημειώσω ότι σχετικά εύκολα μπορούμε να εκτιμήσουμε όσο καλά θέλουμε το ολοκλήρωμα.

Το ολοκλήρωμα είναι

$\displaystyle I=\int_{1}^{2}\ln x \sin x dx -\int_{1}^{2}(x-2)^{2} \sin x dx=I_{1}-I_{2}$

Το $I_{2}$ υπολογίζεται εύκολα .(υπολογίζεται εννοώ με κλειστό τύπο )

Το $I_{1}$ δεν υπολογίζεται .

Αυτό γιατί κάνοντας μια παραγοντική φτάνει στο

$\displaystyle I=\int_{1}^{2}\frac{\ cos x}{x} dx$

Το τελευταίο μπορούμε να το εκτιμήσουμε όσο καλά θέλουμε χρησιμοποιώντας ανισότητες

π.χ $\displaystyle 1-\frac{x^{2}}{2!}< \cos x< 1-\frac{x^{2}}{2!}+\frac{x^{4}}{4!}$

Πάμε να δούμε πως σχολικά μπορούμε να το βγάλουμε μικρότερο από 0,106

.
Εχουμε ότι

$\displaystyle I_{1}=\int_{1}^{2}\ln x \sin x dx \leq \int_{1}^{2}\ln x dx=x \ln x-x|^{2}_{1}=2\ln2-1$

Ενώ

$\displaystyle I_{2}=\int_{1}^{2}(x-2)^{2} \sin x dx\geq \sin 1 \int_{1}^{2}(x-2)^{2}dx=\frac{\sin 1}{3}$

(Αντί για $\sin 1$ θα μπορούσαμε να βάλουμε $\sin \frac{\pi }{4}$ με το ανάλογο κόστος)

Ετσι είναι $I\leq 2\ln 2-1-\frac{\sin1}{3}\leq 0,106$

kfd · #11

Σε μέρος του $\left [ 4/3,\right2]$ η

αρνητική.Πώς από την (3) πολλ/ζω κατά μέλη;

Λάμπρος Κατσάπας · #12

Καθαρογράφω τις λύσεις που πρότεινα παραπάνω.

Η πρώτη λύση δεν χρησιμοποιεί κανένα προηγούμενο υποερώτημα και ιδιότητα της

και ξεπερνά τον σκόπελο

της αλλαγής προσήμου της

στο διάστημα ολοκλήρωσης. Η δεύτερη τα χρησιμοποιεί όλα.

1η Λύση

Για $x \in[1,2]$ είναι $0<\sin x \leq1$ και $f(x)=\ln x-(x-2)^2\leq \ln x$ αφού $-(x-2)^2 \leq 0$ .

Άρα για $x \in[1,2]$ έχουμε $f(x)\sin x\leq \ln x \sin x\leq \ln x\leq \ln2<\ln e =1$ και ολοκληρώνοντας

παίρνουμε το ζητούμενο.

2η Λύση

Η

έχει τις δύο ρίζες της στο (1,2)

και

όπως μπορούμε να ελέγξουμε εύκολα από

Bolzano. Έστω x_0

η ρίζα στο (1,2)

. Μπορούμε να κάνουμε μια εκτίμηση γι'αυτήν αλλά δεν χρειάζεται.

Επίσης f(x)<0

για κάθε $x \in [1,x_0)$ και f(x)>0

για κάθε $x \in (x_0,2]$ . Άρα

$\displaystyle \int_{1}^{2}f(x)\sin x dx <\int_{x_0}^{2}f(x)\sin x dx$ αφού $\displaystyle \int_{1}^{x_0}f(x)\sin x dx <0$

και το τελευταίο ολοκλήρωμα είναι $\displaystyle <\int_{x_0}^{2}(3x-4)\sin x dx <\int_{x_0}^{2}(3x-4) dx=-\frac{3}{2}x_{0}^{2}+4x_{0}-2$

Το τριώνυμο $P(x_0)=-\dfrac{3}{2}x_{0}^{2}+4x_{0}-2$ έχει μέγιστη τιμή $\dfrac{2}{3}$ στο διάστημα

(1,2)

. Επομένως, οπουδήποτε και αν βρίσκεται η ρίζα $x_{0}$ στο (1,2)

το αρχικό

ολοκλήρωμα θα είναι $<\dfrac{2}{3}<1.$

Christos.N · #13

Έχει και το Γ4 ένα ενδιαφέρον (ως προς την ροή των ερωτημάτων), το παραθέτω σε png.

: DeepinScreenshot_select-area_20190514190650.png (36.8 KiB) Προβλήθηκε 1848 φορές

Λάμπρος Κατσάπας · #14

Christos.N έγραψε: ↑
Τρί Μάιος 14, 2019 7:08 pm
Έχει και το Γ4 ένα ενδιαφέρον (ως προς την ροή των ερωτημάτων), το παραθέτω σε png.
DeepinScreenshot_select-area_20190514190650.png

Κάνω το πρώτο.

Έστω

το σημείο τομής των διαγωνίων.

Για $x\in (0,1].$

Από ομοιότητα των τριγώνων AKL,ABD

παίρνουμε $\dfrac{x}{KL}=\dfrac{AO}{BD}\Rightarrow KL=x.$

Άρα $(AKL)=\dfrac{1}{2}x^2.$

Για $x\in (1,2].$

Το συμμετρικό

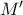του τυχαίου

που φαίνεται στο σχήμα έχει τετμημένη 2-x.

Το εμβαδόν του ρόμβου είναι το ημιγινόμενο των διαγωνίων του δηλαδή

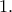
Άρα το γραμοσκιασμένο εμβαδόν στη περίπτωση όπου $x\in (1,2]$ θα είναι $(ABCD)-(GK'L')=1-\dfrac{1}{2}(2-x)^2$

όπου K', L'

τα συμμετρικά των K,L

.

Λάμπρος Κατσάπας · #15

Το Γ4 έχει εξαιρετικά απλή λύση. Την αφήνω για την ώρα μήπως θέλει να ασχοληθεί κάποιος άλλος.

#16

$\displaystyle{0<lnx<ln2<1\Rightarrow 0<ln^2x<1}$
$\displaystyle{0<(x-2)^2<1}$
αρα $\displaystyle{(lnx)^2+(x-2)^2-2<0}$
συνεπως η εξίσωση είναι αδύνατη

Christos.N · #17

Πολύ σωστά Ροδόλφε , η παρατήρηση μου είναι ότι ως ζητούμενο έρχεται κόντρα στην συνολική ανάπτυξη του θέματος.
Ένας άλλος τρόπος:

$\sqrt{ln^2x+(x-2)^2}\leq \sqrt{ln^2x}+\sqrt{(x-2)^2}=lnx+2-x \leq x-1+2-x=1....$

Προσομοίωσης

Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Re: Προσομοίωσης

Μέλη σε σύνδεση