george visvikis έγραψε: ↑Τρί Μαρ 05, 2019 8:07 pm
Στο παρακάτω σχήμα το

είναι ισόπλευρο τρίγωνο πλευράς

και στις πλευρές του

θεωρούμε τα σημεία

αντίστοιχα ώστε

Σημείο

κινείται στον άξονα

έτσι ώστε

Νέου τύπου...png
A) Να εκφράσετε τη διαφορά

ως συνάρτηση του

Β) Έστω

η παραπάνω συνάρτηση:
B1) Nα υπολογίσετε το όριο

.......... B2) Να βρείτε τα ακρότατα της

Β3) Να δείξετε ότι υπάρχει
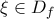
ώστε

Καλησπέρα και Καλή Σαρακοστή
Α) Νόμος συνημητόνων στα τρίγωνα

Οπότε

και

B)

όπως εχει αποδειχθεί παραπάνω

Από το τρίγωνο

Τριγωνική ανισότητα στο τρίγωνο

.Το ίσον ισχύει για συνευθειακά σημεία
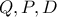
και είναι

Το τρίγωνο

Συνεπώς εχουμε βρεί μέγιστο και ελάχιστο .Θα μελετηθούν πιθανά ακρότατα και στα άλλα σημεία του πεδίου ορισμού της συνάρτησης

Μελέτη των ριζών της

:

Αν

Αν

δεκτή μόνο η τιμή
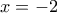
Αρα

Μελέτη του προσήμου της


Αν
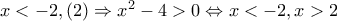
Αρα για

η συνάρτηση

είναι γνησίως αυξουσα
Αν

και η συνάρτηση

είναι γνησίως
φθίνουσα στο διάστημα
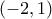
Αν

ομοίως

είναι γνησίως φθίνουσα
Τελικά η συνάρτηση

έχει ελάχιστο στη θεση

και μέγιστο στη θέση

Η λύση για το
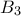
άλλη μέρα εκτός και αν απαντηθεί
Λύση στο
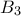
Στο ερώτημα αυτο δίνεται η λύση ΧΩΡΙΣ τα θεμελιώδη θεωρήματα της Γ Λυκείου Μεση Τιμή ,

,κ.λ.π Και όταν λεμε ασκήσεις ΝΕΟΥ ΤΥΠΟΥ εννοούμε δυο βασικούς άξονες
1) Να χρησιμοποιούνται τα Μαθηματικά Των προηγούμενων Τάξεων και η Γεωμετρική εποπτεία
2) Να προσεγγίζουν τις εφαρμογές των Μαθηματικών για να είναι ορατή και η χρησιμότητα των Μαθηματικών
Πιθανόν να είναι και άλλα και να μου διαφευγουν ...μπορεί να ακουστούν και άλλοι προβληματισμοί

,
όπου

![f''(x)=0\Leftrightarrow 4\kappa (x)\sqrt{\kappa (x)}=\sigma (x)\sqrt{\sigma (x)}\Leftrightarrow 4^{2}=(\dfrac{\sigma(x) }{\kappa (x)})^{3}\Leftrightarrow \dfrac{\sigma (x)}{\kappa (x)}=2\sqrt[3]{2}\Leftrightarrow \dfrac{x^{2}-8x+28}{x^{2}-2x+4}=2.\sqrt[3]{2}\Leftrightarrow (1-2.\sqrt[3]{2})x^{2}+(4.\sqrt[3]{2}-8)x+(28-8.\sqrt[3]{2})=0,(*), a=1-2.\sqrt[3]{2},c=28-8.\sqrt[3]{2}, f''(x)=0\Leftrightarrow 4\kappa (x)\sqrt{\kappa (x)}=\sigma (x)\sqrt{\sigma (x)}\Leftrightarrow 4^{2}=(\dfrac{\sigma(x) }{\kappa (x)})^{3}\Leftrightarrow \dfrac{\sigma (x)}{\kappa (x)}=2\sqrt[3]{2}\Leftrightarrow \dfrac{x^{2}-8x+28}{x^{2}-2x+4}=2.\sqrt[3]{2}\Leftrightarrow (1-2.\sqrt[3]{2})x^{2}+(4.\sqrt[3]{2}-8)x+(28-8.\sqrt[3]{2})=0,(*), a=1-2.\sqrt[3]{2},c=28-8.\sqrt[3]{2},](/forum/ext/geomar/texintegr/latexrender/pictures/eef73679b15a0690a9c0a0cb3f957d3f.png)
![4(7-2.\sqrt[3]{2})>0\Leftrightarrow 7^{3}>2^{3}.2,c>0,a<0,a.c<0,\Delta >0 4(7-2.\sqrt[3]{2})>0\Leftrightarrow 7^{3}>2^{3}.2,c>0,a<0,a.c<0,\Delta >0](/forum/ext/geomar/texintegr/latexrender/pictures/d02d243158cef3cb6f6fc7212c4da129.png)
Συνεπώς υπάρχει

Γιάννης
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
 είναι ισόπλευρο τρίγωνο πλευράς
είναι ισόπλευρο τρίγωνο πλευράς  και στις πλευρές του
και στις πλευρές του  θεωρούμε τα σημεία
θεωρούμε τα σημεία αντίστοιχα ώστε
αντίστοιχα ώστε  Σημείο
Σημείο  κινείται στον άξονα
κινείται στον άξονα  έτσι ώστε
έτσι ώστε  A) Να εκφράσετε τη διαφορά
A) Να εκφράσετε τη διαφορά  ως συνάρτηση του
ως συνάρτηση του 
 η παραπάνω συνάρτηση:
η παραπάνω συνάρτηση:  .......... B2) Να βρείτε τα ακρότατα της
.......... B2) Να βρείτε τα ακρότατα της 
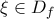 ώστε
ώστε 

 σύμφωνα με τα δεδομένα του προβλήματος.
σύμφωνα με τα δεδομένα του προβλήματος.  που σχηματίζει
που σχηματίζει  γωνία με τον
γωνία με τον  είναι
είναι  και
και  που σχηματίζει
που σχηματίζει  γωνία με τον
γωνία με τον  έτσι για τα
έτσι για τα  ισχύουν αντίστοιχα
ισχύουν αντίστοιχα 
 ή
ή  ή
ή 
 άρα
άρα  οπότε
οπότε  με
με 
 και τότε
και τότε
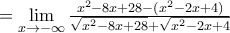




 όπως εχει αποδειχθεί παραπάνω
όπως εχει αποδειχθεί παραπάνω 

 .Το ίσον ισχύει για συνευθειακά σημεία
.Το ίσον ισχύει για συνευθειακά σημεία 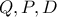 και είναι
και είναι  Το τρίγωνο
Το τρίγωνο  Συνεπώς εχουμε βρεί μέγιστο και ελάχιστο .Θα μελετηθούν πιθανά ακρότατα και στα άλλα σημεία του πεδίου ορισμού της συνάρτησης
Συνεπώς εχουμε βρεί μέγιστο και ελάχιστο .Θα μελετηθούν πιθανά ακρότατα και στα άλλα σημεία του πεδίου ορισμού της συνάρτησης
 :
:

 δεκτή μόνο η τιμή
δεκτή μόνο η τιμή 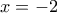



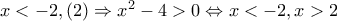
 η συνάρτηση
η συνάρτηση  και η συνάρτηση
και η συνάρτηση 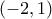
 ομοίως
ομοίως  είναι γνησίως φθίνουσα
είναι γνησίως φθίνουσα 

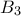 άλλη μέρα εκτός και αν απαντηθεί
άλλη μέρα εκτός και αν απαντηθεί  ,κ.λ.π Και όταν λεμε ασκήσεις ΝΕΟΥ ΤΥΠΟΥ εννοούμε δυο βασικούς άξονες
,κ.λ.π Και όταν λεμε ασκήσεις ΝΕΟΥ ΤΥΠΟΥ εννοούμε δυο βασικούς άξονες  ,
,
![f''(x)=0\Leftrightarrow 4\kappa (x)\sqrt{\kappa (x)}=\sigma (x)\sqrt{\sigma (x)}\Leftrightarrow 4^{2}=(\dfrac{\sigma(x) }{\kappa (x)})^{3}\Leftrightarrow \dfrac{\sigma (x)}{\kappa (x)}=2\sqrt[3]{2}\Leftrightarrow \dfrac{x^{2}-8x+28}{x^{2}-2x+4}=2.\sqrt[3]{2}\Leftrightarrow (1-2.\sqrt[3]{2})x^{2}+(4.\sqrt[3]{2}-8)x+(28-8.\sqrt[3]{2})=0,(*), a=1-2.\sqrt[3]{2},c=28-8.\sqrt[3]{2}, f''(x)=0\Leftrightarrow 4\kappa (x)\sqrt{\kappa (x)}=\sigma (x)\sqrt{\sigma (x)}\Leftrightarrow 4^{2}=(\dfrac{\sigma(x) }{\kappa (x)})^{3}\Leftrightarrow \dfrac{\sigma (x)}{\kappa (x)}=2\sqrt[3]{2}\Leftrightarrow \dfrac{x^{2}-8x+28}{x^{2}-2x+4}=2.\sqrt[3]{2}\Leftrightarrow (1-2.\sqrt[3]{2})x^{2}+(4.\sqrt[3]{2}-8)x+(28-8.\sqrt[3]{2})=0,(*), a=1-2.\sqrt[3]{2},c=28-8.\sqrt[3]{2},](/forum/ext/geomar/texintegr/latexrender/pictures/eef73679b15a0690a9c0a0cb3f957d3f.png)
![4(7-2.\sqrt[3]{2})>0\Leftrightarrow 7^{3}>2^{3}.2,c>0,a<0,a.c<0,\Delta >0 4(7-2.\sqrt[3]{2})>0\Leftrightarrow 7^{3}>2^{3}.2,c>0,a<0,a.c<0,\Delta >0](/forum/ext/geomar/texintegr/latexrender/pictures/d02d243158cef3cb6f6fc7212c4da129.png)
