Παραλλαγή του σχολικού βιβλίου

#1

$\bigstar$ Η συνάρτηση

είναι παραγωγίσιμη στο $\mathbb{R}$ με f(0)=0

και ισχύει $\displaystyle f'(x)\left[ {{e^{f(x)}} + {e^{ - f(x)}}} \right] = 2,$ για κάθε $x\in \mathbb{R}.$

Α) Να βρείτε τον τύπο της

Β) Να υπολογίσετε το ολοκλήρωμα $\displaystyle \int_0^1 {\frac{{1}}{{\sqrt {{x^2} + 1} }}dx}$

Γ) Να υπολογίσετε το όριο $\displaystyle \mathop {\lim }\limits_{x \to + \infty } \frac{{f(x)}}{{\ln x}}$

#2

Καλησπέρα Γιώργο

$\displaystyle \begin{gathered} A)\,\,\,\,\,\,f'(x)\left[ {{e^{f(x)}} + {e^{ - f(x)}}} \right] = 2 \Leftrightarrow \left[ {{e^{f(x)}}f'(x) - {e^{ - f(x)}}[ - f'(x)]} \right] = 2 \Leftrightarrow \hfill \\ \Leftrightarrow {\left[ {{e^{f(x)}} - {e^{ - f(x)}}} \right]^\prime } = (2x)' \Leftrightarrow {e^{f(x)}} - {e^{ - f(x)}} = 2x + c\,\,\,\,\,\,(1) \hfill \\ f(0) = 0 \Rightarrow c = 0 \hfill \\ (1) \Leftrightarrow {e^{f(x)}} - {e^{ - f(x)}} = 2x \Leftrightarrow {\left( {{e^{f(x)}}} \right)^2} - 2x{e^{f(x)}} - 1 = 0 \Leftrightarrow {e^{f(x)}} = \frac{{2x + \sqrt {4{x^2} + 4} }}{2} = x + \sqrt {{x^2} + 1} \Leftrightarrow \hfill \\ \Leftrightarrow f(x) = \ln \left( {x + \sqrt {{x^2} + 1} } \right) \hfill \\ B)\,\,\,\,\,\int\limits_0^1 {\frac{1}{{\sqrt {{x^2} + 1} }}dx} = \int\limits_0^1 {{{\left( {\ln \left( {x + \sqrt {{x^2} + 1} } \right)} \right)}^\prime }dx} = \left[ {\ln \left( {x + \sqrt {{x^2} + 1} } \right)} \right]_0^1 = \ln (1 + \sqrt 2 ) \hfill \\ \Gamma )\,\,\,\,\,\mathop {\lim }\limits_{x \to + \infty } \frac{{f(x)}}{{\ln x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\ln \left( {x + \sqrt {{x^2} + 1} } \right)}}{{\ln x}}\mathop = \limits^{\frac{\infty }{\infty }} \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{1}{{\sqrt {{x^2} + 1} }}}}{{\frac{1}{x}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{x}{{\sqrt {{x^2} + 1} }}\mathop = \limits^{x > 0} \mathop {\lim }\limits_{x \to + \infty } \frac{x}{{x\sqrt {1 + 1/{x^2}} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{\sqrt {1 + 1/{x^2}} }} = 1 \hfill \\ \end{gathered}$

Tolaso J Kos · #3

george visvikis έγραψε: ↑
Κυρ Μαρ 03, 2019 5:32 pm
$\bigstar$ Η συνάρτηση είναι παραγωγίσιμη στο $\mathbb{R}$ με και ισχύει $\displaystyle f'(x)\left[ {{e^{f(x)}} + {e^{ - f(x)}}} \right] = 2,$ για κάθε $x\in \mathbb{R}.$

Α) Να βρείτε τον τύπο της

Β) Να υπολογίσετε το ολοκλήρωμα $\displaystyle \int_0^1 {\frac{{1}}{{\sqrt {{x^2} + 1} }}dx}$

Γ) Να υπολογίσετε το όριο $\displaystyle \mathop {\lim }\limits_{x \to + \infty } \frac{{f(x)}}{{\ln x}}$

(Α) Έχουμε διαδοχικά:

$\displaystyle{\begin{aligned} f'(x) \left ( e^{f(x)} + e^{-f(x)} \right ) = 2 &\Leftrightarrow \left ( e^{f(x)}-e^{-f(x)} \right ) ' = \left ( 2x \right )' \\ &\Leftrightarrow e^{f(x)} -e^{-f(x)} = 2x + c\\ &\!\!\!\!\!\!\!\overset{x=0\Rightarrow c=0}{=\!=\!=\!=\!=\!\Rightarrow } e^{f(x)} -e^{-f(x)} = 2x \\ &\Rightarrow e^{2f(x)} - 1 = 2x e^{f(x)}\\ &\Rightarrow e^{2f(x)}- 2x e^{f(x)} -1 =0 \\ &\Rightarrow \left ( e^{f(x)} \right )^2 - 2x e^{f(x)} + x^2 = 1 + x^2 \\ &\Rightarrow \left ( e^{f(x)}-x \right )^2 = 1+ x^2 \end{aligned}}$
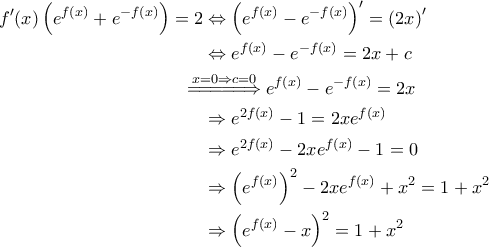
Έστω η συνεχής συνάρτηση $g(x)=e^{f(x)}-x \; ,\; x \in \mathbb{R}$ . Θα δείξουμε ότι η

διατηρεί σταθερό πρόσημο. Ας υποθέσουμε , για να καταλήξουμε σε άτοπο, ότι δε διατηρεί. Συνεπώς θα υπάρχει $x_0 \in \mathbb{R}$ τέτοιο ώστε g(x_0)=0

, δηλ. $e^{f(x_0)}-x_0 =0$ . Τότε:

$\displaystyle{\begin{aligned} e^{f(x_0)} - x_0 =0 &\Leftrightarrow \left ( e^{f(x_0)}-x_0 \right )^2 =0 \\ &\Leftrightarrow 1+x_0^2 =0 \\ &\Leftrightarrow x_0^2=-1 \end{aligned}}$
το οποίο είναι άτοπο. Επιπλέον , είναι g(0)=1>0

άρα

για κάθε $x \in \mathbb{R}$ . Συνεπώς $f(x)= \ln \left( x + \sqrt{x^2+1} \right) \; , \; x \in \mathbb{R}$ . Η συνάρτηση αυτή επαληθεύει τα δεδομένα.

(Β) Από την $(\bigstar)$ είναι:

$\displaystyle{\begin{aligned} f'(x) \left ( e^{f(x)}+e^{-f(x)} \right )=2 &\Leftrightarrow f'(x) \left ( e^{\ln \left ( x + \sqrt{x^2+1} \right )} + e^{-\ln \left ( x+\sqrt{x^2+1} \right )} \right )=2 \\ &\Leftrightarrow f'(x) \left ( x + \sqrt{x^2+1} +\frac{1}{x+\sqrt{x^2+1}} \right )=2 \\ &\Leftrightarrow f'(x) \left ( x + \sqrt{x^2+1} -x + \sqrt{x^2+1} \right )=2 \\ &\Leftrightarrow f'(x) = \frac{1}{\sqrt{x^2+1}} \end{aligned}}$
Άρα:

$\displaystyle{\int_{0}^{1} \frac{\mathrm{d}x}{\sqrt{x^2+1}} = \int_{0}^{1} f'(x) \, \mathrm{d}x = \left [ f(x) \right ]_0^1 = f(1) = \ln \left ( 1+\sqrt{2} \right )}$

(Γ) Έχουμε διαδοχικά εφαρμόζοντας μία φορά DeL' Hospital,

$\displaystyle{\begin{aligned} \ell &= \lim_{x\rightarrow +\infty} \frac{f(x)}{\ln x} \\ &=\lim_{x\rightarrow +\infty} \frac{\ln \left ( x+\sqrt{x^2+1} \right )}{\ln x} \\ &= \lim_{x\rightarrow +\infty} \frac{x}{\sqrt{x^2+1}}\\ &= \lim_{x\rightarrow +\infty} \frac{x}{x\sqrt{1+\frac{1}{x^2}}} \\ &= \lim_{x\rightarrow +\infty} \frac{1}{\sqrt{1+\frac{1}{x^2}}}\\ &= 1 \end{aligned}}$
Καλό βράδυ Γιώργο!

Σημείωση: Δεν είμαι φαν της συμπλήρωσης τετραγώνου , αλλά εδώ αποφεύγω τη βαβούρα με τη διακρίνουσα!

Παραλλαγή του σχολικού βιβλίου

Παραλλαγή του σχολικού βιβλίου

Re: Παραλλαγή του σχολικού βιβλίου

Re: Παραλλαγή του σχολικού βιβλίου

Μέλη σε σύνδεση