 δύο φορές παραγωγίσιμη με
δύο φορές παραγωγίσιμη με να δείξετε ότι
να δείξετε ότι 
Συντονιστής: Καρδαμίτσης Σπύρος
Έστω
 Οπότε
Οπότε  κι επειδή η
κι επειδή η  είναι συνεχής,
είναι συνεχής,
 (αφού ως γνωστόν
(αφού ως γνωστόν  με την ισότητα να ισχύει μόνο για
με την ισότητα να ισχύει μόνο για  )
) άρα
άρα 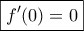
 είναι δυο φορές παραγωγίσιμη, θα έχει συνεχή πρώτη παράγωγο, οπότε
είναι δυο φορές παραγωγίσιμη, θα έχει συνεχή πρώτη παράγωγο, οπότε  και με
και με 
Θα χρησιμοποιήσω το γεγονός ότι
 για κάθε
για κάθε  , με ισότητα αν και μόνον αν
, με ισότητα αν και μόνον αν  (απλό και γνωστό). Επίσης θα χρησιμοποιήσω ότι η
(απλό και γνωστό). Επίσης θα χρησιμοποιήσω ότι η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  .
. .
. , οπότε
, οπότε  .
.  οπότε εξετάζουμε αν υπάρχει το όριο
οπότε εξετάζουμε αν υπάρχει το όριο 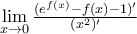 για να δούμε αν εφαρμόζεται ο κανόνας l' Hospital.
για να δούμε αν εφαρμόζεται ο κανόνας l' Hospital.
 . Άρα
. Άρα  , όπως θέλαμε.
, όπως θέλαμε.Θα δώσω μια λύση που το μόνο που χρειάζεται είναι η συνέχεια της
 στο
στο  .
. ότι
ότι 

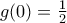
 είναι συνεχής στο
είναι συνεχής στο  .(δύο DHL)
.(δύο DHL) (1)
(1) στο
στο  μας δίνει ότι
μας δίνει ότι 
 στην (1) συμπεραίνουμε ότι το
στην (1) συμπεραίνουμε ότι το
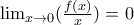
 υπάρχει και
υπάρχει και 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες