- DIAG 2018.pdf
- (187.27 KiB) Μεταφορτώθηκε 1954 φορές
Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Συντονιστής: Καρδαμίτσης Σπύρος
- Τηλέγραφος Κώστας
- Επιμελητής
- Δημοσιεύσεις: 1025
- Εγγραφή: Κυρ Δεκ 21, 2008 12:06 am
- Τοποθεσία: ΦΕΡΕΣ-ΑΛΕΞ/ΠΟΛΗ
- Επικοινωνία:
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Πράγματι, ένα όμορφα διαρθρωμένο επαναληπτικό διαγώνισμα, σχεδιασμένο από τους εκλεκτούς φίλους, τη δουλειά των οποίων γνωρίζουμε καλά στο 
Δημήτρη Ντρίζο, Σχολικό Σύμβουλο ΠΕ03 με έδρα τα Τρίκαλα
Θανάση Καραντάνα, Μαθηματικό του 4ου ΓΕ.Λ Καρδίτσας
Σεραφείμ Σαμορέλη, Μαθηματικό του 8ου ΓΕ.Λ Τρικάλων
Κωνσταντίνο Σερίφη, Μαθηματικό του ΓΕ.Λ Μουζακίου
Σωτήρη Σκοτίδα,Μαθηματικό του 2ου ΓΕ.Λ Καρδίτσας
Βρίσκεται στην ιστοσελίδα της Δ.Δ.Ε. Τρικάλων, ΕΔΩ.
Εκεί θα βρείτε και πολλά άλλα ενδιαφέροντα μαθηματικά θέματα.
Δημήτρη Ντρίζο, Σχολικό Σύμβουλο ΠΕ03 με έδρα τα Τρίκαλα
Θανάση Καραντάνα, Μαθηματικό του 4ου ΓΕ.Λ Καρδίτσας
Σεραφείμ Σαμορέλη, Μαθηματικό του 8ου ΓΕ.Λ Τρικάλων
Κωνσταντίνο Σερίφη, Μαθηματικό του ΓΕ.Λ Μουζακίου
Σωτήρη Σκοτίδα,Μαθηματικό του 2ου ΓΕ.Λ Καρδίτσας
Βρίσκεται στην ιστοσελίδα της Δ.Δ.Ε. Τρικάλων, ΕΔΩ.
Εκεί θα βρείτε και πολλά άλλα ενδιαφέροντα μαθηματικά θέματα.
τελευταία επεξεργασία από Γιώργος Ρίζος σε Σάβ Μάιος 19, 2018 11:02 am, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Εξαιρετικό διαγώνισμα με σεβασμό στο σχολικό βιβλίο αλλά και στους μαθητές που μελετούν καθώς και σε αυτούς με μαθηματικές ικανότητες, αφού ελέγχει σημαντικό μέρος της ύλης και έχει σωστή κατανομή βαθμών.Τα εύσημα στην ομάδα των καθηγητών που το δημιούργησε!!!
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13298
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Ένα πολύ ωραίο διαγώνισμα που καλύπτει το μεγαλύτερο μέρος της ύλης, έχει σωστή, κλιμακωτή δομή και δεν απαιτεί ακροβατισμούς και εξωφρενικά τεχνάσματα. Συγχαρητήρια στους θεματοδότες!
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Το δούλεψα σήμερα με μία μαθήτρια μου. Το βρήκαμε αρκετά καλό με εξαίρεση το θέμα Β το οποίο είχε αρκετές πράξεις απ' ότι φάνηκε. Κατά τα άλλα η δυσκολία του δεν ήταν μεγάλη. Το θέμα Δ το βρήκαμε εξαιρετικό ειδικά το Δ4. Το θέμα Γ είναι θέμα ρουτίνας το οποίο ελέγχει βασικές γνώσεις πάνω στο διαφορικό λογισμό. Όσο για το θέμα Α το ερώτημα Α4 έκρυβε παγίδες μιας και η μαθήτρια τη πάτησε σε αρκετά ερωτήματα. Τα υπόλοιπα του θέματος ήταν κλασσικά.
Κάποια στιγμή θα ανεβάσω τη λύση του θέματος Δ.
Κάποια στιγμή θα ανεβάσω τη λύση του θέματος Δ.
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Γ1. Η συνάρτησηΔΙΑΓΩΝΙΣΜΑ έγραψε:Θέμα Γ
Δίδεται η συνάρτηση.
Γ1. Να μελετηθεί ηως προς τη μονοτονία , τα ακρότατα και την κυρτότητα.
Γ2. Να βρεθεί η εξίσωση της εφαπτομένης της γραφικής παράστασης τηςσε σημείο με τετμημένη
η οποία διέρχεται από την αρχή των αξόνων.
Γ3. Να βρεθούν οι τιμές τουγια τις οποίες ισχύει
.
Γ4. Ανείναι το εμβαδόν του χωρίου που περικλείεται της γραφικής παράστασης της
, του άξονα
και της ευθείας
τότε να δειχθεί ότι
 έχει ρίζα στο
έχει ρίζα στο  και είναι παραγωγίσιμη στο
και είναι παραγωγίσιμη στο  με
με  . Επειδή
. Επειδή  έπεται ότι η
έπεται ότι η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  και παρουσιάζει ολικό ελάχιστο στο
και παρουσιάζει ολικό ελάχιστο στο  ίσο με
ίσο με 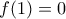 . Η συνάρτηση
. Η συνάρτηση  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο  η οποία είναι θετική για κάθε
η οποία είναι θετική για κάθε  . Άρα η
. Άρα η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  και αυτόματα η
και αυτόματα η  είναι γνήσια φθίνουσα. Άρα η
είναι γνήσια φθίνουσα. Άρα η  είναι γνήσια φθίνουσα και κατά συνέπεια η
είναι γνήσια φθίνουσα και κατά συνέπεια η  είναι κοίλη.
είναι κοίλη.Γ2. Η εφαπτομένη της
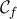 σε τυχόν σημείο
σε τυχόν σημείο  έχει εξίσωση
έχει εξίσωση
Για να διέρχεται η
 από την αρχή των αξόνων πρέπει το σημείο
από την αρχή των αξόνων πρέπει το σημείο  να επαληθεύει την εξίσωση. Συνεπώς:
να επαληθεύει την εξίσωση. Συνεπώς:
Άρα το ζητούμενο σημείο είναι το
 και η εξίσωση της εφαπτομένης στο σημείο αυτό είναι η
και η εξίσωση της εφαπτομένης στο σημείο αυτό είναι η
Γ3. Έχουμε διαδοχικά:
![\displaystyle{\begin{aligned}
f^2(x) \leq f(x) &\Leftrightarrow f^2(x) - f(x) \leq 0 \\
&\Leftrightarrow f(x) \left ( f(x) -1 \right ) \leq 0 \\
&\Leftrightarrow x \in [1, e]
\end{aligned}} \displaystyle{\begin{aligned}
f^2(x) \leq f(x) &\Leftrightarrow f^2(x) - f(x) \leq 0 \\
&\Leftrightarrow f(x) \left ( f(x) -1 \right ) \leq 0 \\
&\Leftrightarrow x \in [1, e]
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/3de00666aad9a593ae6edd5245000e24.png)
το οποίο έπεται από πίνακα προσήμου.
Γ4. Επειδή η
 είναι κοίλη αυτό σημαίνει ότι το γράφημα της
είναι κοίλη αυτό σημαίνει ότι το γράφημα της  βρίσκεται κάτω από το γράφημα της εφαπτομένης με εξαίρεση το σημείο το επαφής. Το εμβαδόν που περικλείεται της γραφικής παράστασης της
βρίσκεται κάτω από το γράφημα της εφαπτομένης με εξαίρεση το σημείο το επαφής. Το εμβαδόν που περικλείεται της γραφικής παράστασης της  , του άξονα
, του άξονα  και της ευθείας
και της ευθείας  είναι ίσο με
είναι ίσο με ![\displaystyle{\mathrm{E} = \int_{1}^{e} \left | f(t) \right | \, \mathrm{d}t \overset{f(t)>0 \quad \text{\gr για κάθε} \; \; x \in [1, e]}{=\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\!} \int_{1}^{e} f(t) \, \mathrm{d}t} \displaystyle{\mathrm{E} = \int_{1}^{e} \left | f(t) \right | \, \mathrm{d}t \overset{f(t)>0 \quad \text{\gr για κάθε} \; \; x \in [1, e]}{=\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\! =\!} \int_{1}^{e} f(t) \, \mathrm{d}t}](/forum/ext/geomar/texintegr/latexrender/pictures/effaf0c63e3ec081ed82314923b2ce27.png)
Συνδυάζοντας τα ερωτήματα Γ2, Γ3 καθώς και το γεγονός ότι η ισότητα στο ερώτημα Γ3 ισχύει σε μόνο δύο σημεία έχουμε ότι:

και το ζητούμενο έπεται.
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
ΔΙΑΓΩΝΙΣΜΑ έγραψε: Θέμα Δ
Δίδονται οι συναρτήσειςκαι
.
Δ1. Να μελετηθεί ηως προς τη μονοτονία και την κυρτότητα και να βρεθούν , αν υπάρχουν , τα σημεία καμπής της γραφικής παράστασης.
Δ2. Να δειχθεί ότι ηείναι συνεχής και γνησίως αύξουσα.
Δ3. Να βρεθεί το όριο.
Δ4. Θεωρούμε τα σημεία,
και
όπου
. Να δειχθεί ότι:
(i) τα σημείαδεν είναι συνευθειακά.
(ii) υπάρχειτέτοιο ώστε
όπου
το εμβαδόν του τριγώνου
.
Δ1. Η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο  η οποία είναι καθαρά θετική στο
η οποία είναι καθαρά θετική στο  άρα η
άρα η  είναι γνήσια αύξουσα. Επιπλέον, η
είναι γνήσια αύξουσα. Επιπλέον, η  είναι παραγωγίσιμη με ποράγωγο
είναι παραγωγίσιμη με ποράγωγο  . Θεωρούμε συνάρτηση
. Θεωρούμε συνάρτηση  και παρατηρούμε ότι
και παρατηρούμε ότι  . Η
. Η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο
Διαπιστώνουμε ότι
 για κάθε
για κάθε  άρα η
άρα η  είναι γνήσια αύξουσα. Οπότε
είναι γνήσια αύξουσα. Οπότε  για κάθε
για κάθε  και
και  για κάθε
για κάθε  . Συνεπώς η
. Συνεπώς η  είναι κυρτή στο
είναι κυρτή στο  και κοίλη στο
και κοίλη στο ![(-1, 0] (-1, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/00f150054838129390a50021604df5af.png) . Το σημείο
. Το σημείο  είναι σημείο καμπής.
είναι σημείο καμπής. Δ2. Αρκεί να δείξω ότι
 . Πράγματι,
. Πράγματι,
Η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο
Θεωρούμε συνάρτηση
 και παρατηρούμε ότι
και παρατηρούμε ότι  . Η
. Η 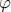 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο
Άρα
 για κάθε
για κάθε 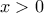 . Οπότε η
. Οπότε η 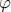 είναι γνήσια αύξουσα και μάλιστα θετική. Άρα η
είναι γνήσια αύξουσα και μάλιστα θετική. Άρα η  είναι γνήσια αύξουσα όπως θέλαμε.
είναι γνήσια αύξουσα όπως θέλαμε.Δ3. Έχουμε:

αφού με DLH βγάζουμε
 .
.Δ4.
(i) Θεωρούμε τα διανύσματα
 . Ελέγχουμε την ορίζουσα
. Ελέγχουμε την ορίζουσα![\displaystyle{\det \left ( \overrightarrow{\mathrm{OA}} , \overrightarrow{\mathrm{OB}} \right ) = \begin{vmatrix}
a & a+1 \\
f(a) & f(a+1)
\end{vmatrix} = a f(a+1) - (a+1) f(a) = a (a+1) \left [ \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \right ] \neq 0 } \displaystyle{\det \left ( \overrightarrow{\mathrm{OA}} , \overrightarrow{\mathrm{OB}} \right ) = \begin{vmatrix}
a & a+1 \\
f(a) & f(a+1)
\end{vmatrix} = a f(a+1) - (a+1) f(a) = a (a+1) \left [ \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \right ] \neq 0 }](/forum/ext/geomar/texintegr/latexrender/pictures/2388ccca8e7b555500029aaa0b19c416.png)
διότι αφού η
 είναι γνήσια αύξουσα θα είναι
είναι γνήσια αύξουσα θα είναι  . Το συμπέρασμα έπεται.
. Το συμπέρασμα έπεται.(ii) Το εμβαδόν του τριγώνου
 είναι ίσο με:
είναι ίσο με:![\displaystyle{\left ( \mathrm{OAB} \right ) = \frac{1}{2} \left | \begin{vmatrix}
a & a+1\\
f(a) & f(a+1)
\end{vmatrix} \right | = \frac{1}{2} a (a+1) \left [ \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \right ]} \displaystyle{\left ( \mathrm{OAB} \right ) = \frac{1}{2} \left | \begin{vmatrix}
a & a+1\\
f(a) & f(a+1)
\end{vmatrix} \right | = \frac{1}{2} a (a+1) \left [ \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/23640fa23c5b8c00d8ef7ad6501ab091.png)
Άρα η ζητούμενη σχέση γράφεται
![\displaystyle{
\begin{aligned}\left ( \mathrm{OAB} \right ) = \frac{a (a+1)}{2} g'(\xi) &\Leftrightarrow \frac{1}{2} a (a+1) \left [ \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \right ] = \frac{a(a+1)}{2} g'(\xi)\\
&\Leftrightarrow g'(\xi) = \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \\
&\Leftrightarrow g'(\xi) = \frac{g(a+1)-g(a)}{a+1-a}
\end{aligned}} \displaystyle{
\begin{aligned}\left ( \mathrm{OAB} \right ) = \frac{a (a+1)}{2} g'(\xi) &\Leftrightarrow \frac{1}{2} a (a+1) \left [ \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \right ] = \frac{a(a+1)}{2} g'(\xi)\\
&\Leftrightarrow g'(\xi) = \frac{f(a+1)}{a+1} - \frac{f(a)}{a} \\
&\Leftrightarrow g'(\xi) = \frac{g(a+1)-g(a)}{a+1-a}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/1c728249e473eea0728df14f54a18f5e.png)
Το συμπέρασμα έπεται από ΘΜΤ στη συνάρτηση
 στο διάστημα
στο διάστημα ![[a, a+1] [a, a+1]](/forum/ext/geomar/texintegr/latexrender/pictures/f6abcb6e04861a4e7b7df0a1ed2d566c.png) .
.ΚΑΤΑΠΛΗΚΤΙΚΟ ΘΕΜΑ!!
τελευταία επεξεργασία από Tolaso J Kos σε Κυρ Μάιος 20, 2018 1:43 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Η φαντασία είναι σημαντικότερη από τη γνώση !


- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Καλησπέρα σε όλους. Μια ακόμα προσέγγιση στο Δ4 ii, με περισσότερη γεωμετρική εποπτεία, δίχως Αναλυτική Γεωμετρία.
Από τη μελέτη της συνάρτησης έχουμε το σχήμα
έχουμε το σχήμα
Οπότε είναι
 .
.
(ΣΧΟΛΙΟ: πολλαπλασιάσαμε και διαιρέσαμε με , για να φέρουμε την παράσταση σε κατάλληλη μορφή, κοιτώντας πού θέλουμε να καταλήξουμε).
, για να φέρουμε την παράσταση σε κατάλληλη μορφή, κοιτώντας πού θέλουμε να καταλήξουμε).
Όμως, από το Θ.Μ.Τ για την συνάρτηση στο
στο ![\displaystyle \left[ {\alpha ,\alpha + 1} \right] \displaystyle \left[ {\alpha ,\alpha + 1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/4e7b85d2c5627e67357ad029f5f82e57.png) έχουμε ότι υπάρχει
έχουμε ότι υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  ,
,
οπότε .
.
Από τη μελέτη της συνάρτησης
 έχουμε το σχήμα
έχουμε το σχήμαΟπότε είναι

 .
.(ΣΧΟΛΙΟ: πολλαπλασιάσαμε και διαιρέσαμε με
 , για να φέρουμε την παράσταση σε κατάλληλη μορφή, κοιτώντας πού θέλουμε να καταλήξουμε).
, για να φέρουμε την παράσταση σε κατάλληλη μορφή, κοιτώντας πού θέλουμε να καταλήξουμε).Όμως, από το Θ.Μ.Τ για την συνάρτηση
 στο
στο ![\displaystyle \left[ {\alpha ,\alpha + 1} \right] \displaystyle \left[ {\alpha ,\alpha + 1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/4e7b85d2c5627e67357ad029f5f82e57.png) έχουμε ότι υπάρχει
έχουμε ότι υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  ,
,οπότε
 .
.- exdx
- Επιμελητής
- Δημοσιεύσεις: 1746
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Δ2) Παραλλαγή
 , αφού η
, αφού η  είναι γνησίως αύξουσα
είναι γνησίως αύξουσα
Εφαρμόστηκε το ΘΜΤ στο![\displaystyle [0,x] \displaystyle [0,x]](/forum/ext/geomar/texintegr/latexrender/pictures/83fc3d442a32c5248bd0ad706069170c.png)
Δ4 i) Αν τα ήταν συνευθειακά θα ανήκαν στην
ήταν συνευθειακά θα ανήκαν στην  , οπότε
, οπότε  και έτσι
και έτσι
 , (εφαρμόστηκε δύο γορές το ΘΜΤ) ,
, (εφαρμόστηκε δύο γορές το ΘΜΤ) ,
άτοπο αφού η είναι γνησίως αύξουσα .
ii) Η συνάρτηση είναι γνησίως αύξουσα και κυρτή. Οι χορδές
είναι γνησίως αύξουσα .
ii) Η συνάρτηση είναι γνησίως αύξουσα και κυρτή. Οι χορδές  είναι πάνω από τη γραφική παράσταση (Με απόδειξη)
είναι πάνω από τη γραφική παράσταση (Με απόδειξη)

Οπότε :

Με ΘΜΤ εξασφαλίζεται η ύπαρξη του .
.
(Στο ίδιο πνεύμα με το Γιώργο )
 , αφού η
, αφού η  είναι γνησίως αύξουσα
είναι γνησίως αύξουσα Εφαρμόστηκε το ΘΜΤ στο
![\displaystyle [0,x] \displaystyle [0,x]](/forum/ext/geomar/texintegr/latexrender/pictures/83fc3d442a32c5248bd0ad706069170c.png)
Δ4 i) Αν τα
 ήταν συνευθειακά θα ανήκαν στην
ήταν συνευθειακά θα ανήκαν στην  , οπότε
, οπότε  και έτσι
και έτσι  , (εφαρμόστηκε δύο γορές το ΘΜΤ) ,
, (εφαρμόστηκε δύο γορές το ΘΜΤ) ,άτοπο αφού η
 είναι γνησίως αύξουσα .
ii) Η συνάρτηση είναι γνησίως αύξουσα και κυρτή. Οι χορδές
είναι γνησίως αύξουσα .
ii) Η συνάρτηση είναι γνησίως αύξουσα και κυρτή. Οι χορδές  είναι πάνω από τη γραφική παράσταση (Με απόδειξη)
είναι πάνω από τη γραφική παράσταση (Με απόδειξη)
Οπότε :

Με ΘΜΤ εξασφαλίζεται η ύπαρξη του
 .
.(Στο ίδιο πνεύμα με το Γιώργο )
Kαλαθάκης Γιώργης
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Πάμε να δούμε και το πρώτο θέμα θεωρίας ....
Α1. Απόδειξη θεωρήματος
 η οποία προφανώς δεν είναι γνήσια μονότονη αφού στο
η οποία προφανώς δεν είναι γνήσια μονότονη αφού στο  είναι γνήσια φθίνουσα ενώ στο
είναι γνήσια φθίνουσα ενώ στο ![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png) είναι γνήσια αύξουσα. Είναι , όμως ,
είναι γνήσια αύξουσα. Είναι , όμως ,  αφού
αφού ![\displaystyle{f\left ( \left ( 0, +\infty \right ) \right ) \cap f \left ( \left ( -\infty, 0 \right ] \right ) = \varnothing} \displaystyle{f\left ( \left ( 0, +\infty \right ) \right ) \cap f \left ( \left ( -\infty, 0 \right ] \right ) = \varnothing}](/forum/ext/geomar/texintegr/latexrender/pictures/3cd54d99d070a527ff01471312398355.png) .
.
A3. Διατύπωση ορισμού κατακόρυφης ασύμπτωτης.
Α1. Απόδειξη θεωρήματος
O ισχυρισμός είναι ψευδής. Ας θεωρήσουμε τη συνάρτησηΔΙΑΓΩΝΙΣΜΑ έγραψε:
Α2.
Θεωρήστε τον παρακάτω ισχυρισμό:
Κάθε συνάρτησηείναι και γνησίως μονότονη.
- Να χαρακτηρίσετε τον παραπάνω ισχυρισμό , γράφοντας στο τετράδιό σας το γράμμα Α αν είναι αληθής ή το γράμμα Ψ αν είναι ψευδής.
- Να αιτιολογήσετε την απάντησή σας στο ερώτημα i.
 η οποία προφανώς δεν είναι γνήσια μονότονη αφού στο
η οποία προφανώς δεν είναι γνήσια μονότονη αφού στο  είναι γνήσια φθίνουσα ενώ στο
είναι γνήσια φθίνουσα ενώ στο ![(-\infty, 0] (-\infty, 0]](/forum/ext/geomar/texintegr/latexrender/pictures/8bb8e3006289394bd593c5b7a4904dd6.png) είναι γνήσια αύξουσα. Είναι , όμως ,
είναι γνήσια αύξουσα. Είναι , όμως ,  αφού
αφού ![\displaystyle{f\left ( \left ( 0, +\infty \right ) \right ) \cap f \left ( \left ( -\infty, 0 \right ] \right ) = \varnothing} \displaystyle{f\left ( \left ( 0, +\infty \right ) \right ) \cap f \left ( \left ( -\infty, 0 \right ] \right ) = \varnothing}](/forum/ext/geomar/texintegr/latexrender/pictures/3cd54d99d070a527ff01471312398355.png) .
. A3. Διατύπωση ορισμού κατακόρυφης ασύμπτωτης.
ΔΙΑΓΩΝΙΣΜΑ έγραψε:
A4.
Να χαρακτηριστούν οι παρακάτω προτάσεις ως σωστές ή λανθασμένες γράφοντας στο τετράδιό σας τη λέξη Σωστό αν η πρόταση είναι σωστή ή Λάθος αν πρόταση είναι λάθος.
- Έστω μία συνάρτηση
ορισμένη σε ένα διάστημα
. Τα εσωτερικά σημεία
του
για τα οποία ισχύει
δεν είναι θέσεις σημείων καμπής της γραφικής παράστασης της
.
- Αν μία συνάρτηση
είναι συνεχής στο
τότε και η συνάρτηση
είναι συνεχής στο
.
- Αν μία συνάρτηση
είναι συνεχής σε ένα διάστημα
τότε η
παίρνει πάντοτε στο
μία ελάχιστη τιμή.
- Έστω
μία συνεχής συνάρτηση σε ένα διάστημα
. Αν
για κάθε
και η
δεν είναι παντού μηδέν στο διάστημα
τότε
.
- Έστω μία συνάρτηση
. Αν η
παρουσιάζει τοπικό ακρότατο στο σημείο
και είναι παραγωγίσιμη στο σημείο αυτό τότε υποχρεωτικά είναι
.
- Λ
- Σ
- Λ
- Σ
- Λ ( το Θεώρημα Fermat δεν ισχύει σε άκρο κλειστού διαστήματος )
Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Εξαιρετικό το διαγώνισμα , ευχαριστούμε!
1. Δεν διδάσκουμε με αυτό που λέμε και κάνουμε. Διδάσκουμε με αυτό που είμαστε.
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
2. Ο μέτριος δάσκαλος περιγράφει. Ο καλός δάσκαλος εξηγεί. Ο σωστός δάσκαλος αποδεικνύει. Ο σπουδαίος δάσκαλος εμπνέει. ( Γουίλιαμ Γουάρντ)
-
Νίκος Ζαφειρόπουλος
- Δημοσιεύσεις: 303
- Εγγραφή: Κυρ Απρ 12, 2009 1:06 am
- Τοποθεσία: ΖΑΚΥΝΘΟΣ
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Tolaso J Kos έγραψε: ↑Κυρ Μάιος 20, 2018 2:07 pm
ΔΙΑΓΩΝΙΣΜΑ έγραψε:
A4.
Να χαρακτηριστούν οι παρακάτω προτάσεις ως σωστές ή λανθασμένες γράφοντας στο τετράδιό σας τη λέξη Σωστό αν η πρόταση είναι σωστή ή Λάθος αν πρόταση είναι λάθος.
- Έστω μία συνάρτηση
ορισμένη σε ένα διάστημα
. Τα εσωτερικά σημεία
του
για τα οποία ισχύει
δεν είναι θέσεις σημείων καμπής της γραφικής παράστασης της
.
- Αν μία συνάρτηση
είναι συνεχής στο
τότε και η συνάρτηση
είναι συνεχής στο
.
- Αν μία συνάρτηση
είναι συνεχής σε ένα διάστημα
τότε η
παίρνει πάντοτε στο
μία ελάχιστη τιμή.
- Έστω
μία συνεχής συνάρτηση σε ένα διάστημα
. Αν
για κάθε
και η
δεν είναι παντού μηδέν στο διάστημα
τότε
.
- Έστω μία συνάρτηση
. Αν η
παρουσιάζει τοπικό ακρότατο στο σημείο
και είναι παραγωγίσιμη στο σημείο αυτό τότε υποχρεωτικά είναι
.
- Λ
- Σ
- Λ
- Σ
- Λ ( το Θεώρημα Fermat δεν ισχύει σε άκρο κλειστού διαστήματος )
Το (i) γιατί είναι λάθος;
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Από τη βιασύνη μου... Σωστό είναι ... αφού δε μηδενίζεται δε πρόκειται να είναι καμπή.
Η φαντασία είναι σημαντικότερη από τη γνώση !


-
Νίκος Ζαφειρόπουλος
- Δημοσιεύσεις: 303
- Εγγραφή: Κυρ Απρ 12, 2009 1:06 am
- Τοποθεσία: ΖΑΚΥΝΘΟΣ
- Επικοινωνία:
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Δεν έχει σημασία αν τοTolaso J Kos έγραψε: ↑Σάβ Μάιος 19, 2018 2:14 pmΓ1. Η συνάρτησηέχει ρίζα στο
και είναι παραγωγίσιμη στο
με
. Επειδή
έπεται ότι η
είναι γνήσια αύξουσα στο

 είναι ρίζα της
είναι ρίζα της  . Για να είναι η
. Για να είναι η  γνησίως αύξουσα στο
γνησίως αύξουσα στο  , εκτός από το
, εκτός από το  στο
στο  , πρέπει να αναφερθεί και η συνέχεια της συνάρτησης στο
, πρέπει να αναφερθεί και η συνέχεια της συνάρτησης στο 
Αυτό γενικά δεν είναι σωστό. Π.χ. ηTolaso J Kos έγραψε: ↑Σάβ Μάιος 19, 2018 2:14 pmηείναι γνήσια αύξουσα στο
και αυτόματα η
είναι γνήσια φθίνουσα.
 είναι γνησίως αύξουσα στο πεδίο ορισμού της, αλλά η
είναι γνησίως αύξουσα στο πεδίο ορισμού της, αλλά η  δεν είναι γνησίως φθίνουσα στο πεδίο ορισμού της.
δεν είναι γνησίως φθίνουσα στο πεδίο ορισμού της.-
nikolaos p.
- Δημοσιεύσεις: 277
- Εγγραφή: Δευ Φεβ 14, 2011 11:44 pm
-
Θωμάς Ποδηματάς
- Δημοσιεύσεις: 371
- Εγγραφή: Κυρ Σεπ 25, 2011 9:23 pm
- Τοποθεσία: Βόλος Μαγνησίας
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Χαιρετώ ξανά την εκλεκτή παρέα του 
Είχα πραγματικά καιρό να δω ένα τέτοιο διαγώνισμα ! Απερίφραστα ΣΥΓΧΑΡΗΤΗΡΙΑ στους θεματοδότες !
Ευχαριστούμε θερμά !
Είχα πραγματικά καιρό να δω ένα τέτοιο διαγώνισμα ! Απερίφραστα ΣΥΓΧΑΡΗΤΗΡΙΑ στους θεματοδότες !
Ευχαριστούμε θερμά !
Τους Λαιστρυγόνας και τους Κύκλωπας,
τον άγριο Ποσειδώνα δεν θα συναντήσεις,
αν δεν τους κουβανείς μες την ψυχή σου,
αν η ψυχή σου δεν τους στήνει εμπρός σου
(ΙΘΑΚΗ - Κ.Π. ΚΑΒΑΦΗΣ)
τον άγριο Ποσειδώνα δεν θα συναντήσεις,
αν δεν τους κουβανείς μες την ψυχή σου,
αν η ψυχή σου δεν τους στήνει εμπρός σου
(ΙΘΑΚΗ - Κ.Π. ΚΑΒΑΦΗΣ)
- Λάμπρος Μπαλός
- Δημοσιεύσεις: 984
- Εγγραφή: Τρί Αύγ 13, 2013 12:21 pm
- Τοποθεσία: Τρίκαλα
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Συγχαρητήρια για την εξαιρετική δουλειά. Το βρήκα πολύ εύστοχο το διαγώνισμα. Μου άρεσε και μακάρι να βλέπαμε κάτι τέτοιο και στις πανελλαδικές. Ίσως μόνο αν ήταν ακόμη πιο στρωτό το 2ο θέμα(μην ξεχνάμε και τον αδύνατο μαθητή) να ήταν σούπερ. Μπράβο και πάλι!
Λάμπρος Μπαλός
lamprosbalos81@gmail.com
lamprosbalos81@gmail.com
-
Θωμάς Ποδηματάς
- Δημοσιεύσεις: 371
- Εγγραφή: Κυρ Σεπ 25, 2011 9:23 pm
- Τοποθεσία: Βόλος Μαγνησίας
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Καλησπέρα στην εκλεκτή παρέα του 
Συνάδελφοι το διαγώνισμα ήταν ΕΞΑΙΡΕΤΙΚΟ !


Μακάρι να βλέπαμε τέτοια θέματα στις Εξετάσεις, θέματα που να σε οδηγούν όπως το υπέροχο Γ4 και όχι μόνο
Όσον αφορά στα σχόλια για τη δυσκολία του Β θέματος, προσωπικά δε με βρίσκουν σύμφωνο. Τα θέματα των προηγούμενων ετών, ήταν φορές που ήταν απίστευτα απαράδεκτα, όπως το 2014 που έγραφε η μικρή μου κόρη. Θέματα τόσο απλά επιτίθενται στο διαβασμένο μαθητή, αφού τον εξομοιώνουν με τον μαθητή που απλά έχει εικόνα του αντικειμένου. Βέβαια, το ίδιο ακριβώς ισχύει και για τα απαράδεκτα θέματα, όπως το Β3 του 2013, από την "ανάποδη" πλευρά τώρα, αφού η αδυναμία λύσης του από το σύνολο των εξεταζομένων, δίνει τη δυνατότητα στον ΑΠΟΛΥΤΑ άσχετο να πει "έλα μωρέ, εγώ άμα είχα διαβάσει θα το γραφα"... Φράση η οποία με εκνευρίζει απίστευτα... διότι ου γαρ οίδασι τι λέγουσι ...
Κατά την εκτίμησή μου, τα θέματα των εξετάσεων, θα πρέπει να είναι τέτοια ώστε, ο διαβασμένος που έχει αντιληφθεί το αντικείμενο, να γράφει περίπου 80 κοιτώντας ... το ταβάνι και - αυτό είναι το ωραίο - ΤΑΥΤΟΧΡΟΝΑ ΜΕ ΤΑ ΙΔΙΑ ΘΕΜΑΤΑ, ο αδιάβαστος να νομίζει ότι γράφει άλλο μάθημα !!!
Το Β θέμα του διαγωνίσματος αυτού, εξέταζε σχεδόν όλη την Ύλη εκτός ολοκληρωμάτων βέβαια. Δεν είχε εκτός πνεύματος λογισμό και αν κάποιος έγραφε τη συνάρτηση θα είχε πραγματικά ελάχιστες πράξεις ! Τόσο στον προσδιορισμό των σταθερών όσο και στα κοινά σημεία όσο και στην παραγώγιση για την εύρεση της κοινής εφαπτομένης. Στο
θα είχε πραγματικά ελάχιστες πράξεις ! Τόσο στον προσδιορισμό των σταθερών όσο και στα κοινά σημεία όσο και στην παραγώγιση για την εύρεση της κοινής εφαπτομένης. Στο  δεν ήταν ανάγκη να αντικατασταθούν οι συναρτήσεις, παρά μόνο η απαλοιφή των παρονομαστών. Διαφωνώ στο ότι είχε λογισμό ή στο ότι ήταν βαρύ.
δεν ήταν ανάγκη να αντικατασταθούν οι συναρτήσεις, παρά μόνο η απαλοιφή των παρονομαστών. Διαφωνώ στο ότι είχε λογισμό ή στο ότι ήταν βαρύ.
Το Γ θέμα... κλασσικό μέχρι το Γ4... όπως θα έπρεπε η ανισότητα των ολοκληρωμάτων, αφού πρέπει ο θεματοδότης να αφήνει ίχνη για τη σκέψη του, αλλιώς ψάχνει κανείς για μάγους ή για βοηθούς φακίρηδων
όπως θα έπρεπε η ανισότητα των ολοκληρωμάτων, αφού πρέπει ο θεματοδότης να αφήνει ίχνη για τη σκέψη του, αλλιώς ψάχνει κανείς για μάγους ή για βοηθούς φακίρηδων 
Το Δ θέμα... δεν ήταν καθόλου ανάγκη να γίνει αντικατάσταση για τη μελέτη της μονοτονίας της συνάρτησης αντικατάσταση η οποία οδηγεί σε αρκετό λογισμό, για τον οποίον δεν υπάρχει αναγκαιότητα. Μπορούσε κανείς να δουλέψει με τη συνάρτηση
αντικατάσταση η οποία οδηγεί σε αρκετό λογισμό, για τον οποίον δεν υπάρχει αναγκαιότητα. Μπορούσε κανείς να δουλέψει με τη συνάρτηση  με
με  για κάθε
για κάθε  ... θα τελείωνε αμέσως...
... θα τελείωνε αμέσως...
Δ3 Θέτοντας οδηγείται άμεσα σε κλασσικό όριο.. Αλλά νομίζω πραγματικά ότι το κερασάκι στην τούρτα είναι το Δ4... Το Δ4 πρέπει να είναι για το απόλυτο άριστα και ΕΙΝΑΙ για το απόλυτο άριστα... είτε γεωμετρικά είτε με τον τύπο του εμβαδού, όπως θέλει κανείς
οδηγείται άμεσα σε κλασσικό όριο.. Αλλά νομίζω πραγματικά ότι το κερασάκι στην τούρτα είναι το Δ4... Το Δ4 πρέπει να είναι για το απόλυτο άριστα και ΕΙΝΑΙ για το απόλυτο άριστα... είτε γεωμετρικά είτε με τον τύπο του εμβαδού, όπως θέλει κανείς
Δεν σας κουράζω άλλο. Επαναλαμβάνω την προσωπική μου εκτίμηση : ΕΞΑΙΡΕΤΙΚΟ !
ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΟΛΟΨΥΧΑ ΣΕ ΟΛΟΥΣ, ΕΚΠΑΙΔΕΥΤΙΚΟΥΣ ΚΑΙ ΑΓΩΝΙΖΟΜΕΝΗ ΝΕΟΛΑΙΑ !!!
Συνάδελφοι το διαγώνισμα ήταν ΕΞΑΙΡΕΤΙΚΟ !
Μακάρι να βλέπαμε τέτοια θέματα στις Εξετάσεις, θέματα που να σε οδηγούν όπως το υπέροχο Γ4 και όχι μόνο
Όσον αφορά στα σχόλια για τη δυσκολία του Β θέματος, προσωπικά δε με βρίσκουν σύμφωνο. Τα θέματα των προηγούμενων ετών, ήταν φορές που ήταν απίστευτα απαράδεκτα, όπως το 2014 που έγραφε η μικρή μου κόρη. Θέματα τόσο απλά επιτίθενται στο διαβασμένο μαθητή, αφού τον εξομοιώνουν με τον μαθητή που απλά έχει εικόνα του αντικειμένου. Βέβαια, το ίδιο ακριβώς ισχύει και για τα απαράδεκτα θέματα, όπως το Β3 του 2013, από την "ανάποδη" πλευρά τώρα, αφού η αδυναμία λύσης του από το σύνολο των εξεταζομένων, δίνει τη δυνατότητα στον ΑΠΟΛΥΤΑ άσχετο να πει "έλα μωρέ, εγώ άμα είχα διαβάσει θα το γραφα"... Φράση η οποία με εκνευρίζει απίστευτα... διότι ου γαρ οίδασι τι λέγουσι ...
Κατά την εκτίμησή μου, τα θέματα των εξετάσεων, θα πρέπει να είναι τέτοια ώστε, ο διαβασμένος που έχει αντιληφθεί το αντικείμενο, να γράφει περίπου 80 κοιτώντας ... το ταβάνι και - αυτό είναι το ωραίο - ΤΑΥΤΟΧΡΟΝΑ ΜΕ ΤΑ ΙΔΙΑ ΘΕΜΑΤΑ, ο αδιάβαστος να νομίζει ότι γράφει άλλο μάθημα !!!
Το Β θέμα του διαγωνίσματος αυτού, εξέταζε σχεδόν όλη την Ύλη εκτός ολοκληρωμάτων βέβαια. Δεν είχε εκτός πνεύματος λογισμό και αν κάποιος έγραφε τη συνάρτηση
 θα είχε πραγματικά ελάχιστες πράξεις ! Τόσο στον προσδιορισμό των σταθερών όσο και στα κοινά σημεία όσο και στην παραγώγιση για την εύρεση της κοινής εφαπτομένης. Στο
θα είχε πραγματικά ελάχιστες πράξεις ! Τόσο στον προσδιορισμό των σταθερών όσο και στα κοινά σημεία όσο και στην παραγώγιση για την εύρεση της κοινής εφαπτομένης. Στο  δεν ήταν ανάγκη να αντικατασταθούν οι συναρτήσεις, παρά μόνο η απαλοιφή των παρονομαστών. Διαφωνώ στο ότι είχε λογισμό ή στο ότι ήταν βαρύ.
δεν ήταν ανάγκη να αντικατασταθούν οι συναρτήσεις, παρά μόνο η απαλοιφή των παρονομαστών. Διαφωνώ στο ότι είχε λογισμό ή στο ότι ήταν βαρύ.Το Γ θέμα... κλασσικό μέχρι το Γ4...
Το Δ θέμα... δεν ήταν καθόλου ανάγκη να γίνει αντικατάσταση για τη μελέτη της μονοτονίας της συνάρτησης
 αντικατάσταση η οποία οδηγεί σε αρκετό λογισμό, για τον οποίον δεν υπάρχει αναγκαιότητα. Μπορούσε κανείς να δουλέψει με τη συνάρτηση
αντικατάσταση η οποία οδηγεί σε αρκετό λογισμό, για τον οποίον δεν υπάρχει αναγκαιότητα. Μπορούσε κανείς να δουλέψει με τη συνάρτηση  με
με  για κάθε
για κάθε  ... θα τελείωνε αμέσως...
... θα τελείωνε αμέσως... Δ3 Θέτοντας
 οδηγείται άμεσα σε κλασσικό όριο.. Αλλά νομίζω πραγματικά ότι το κερασάκι στην τούρτα είναι το Δ4... Το Δ4 πρέπει να είναι για το απόλυτο άριστα και ΕΙΝΑΙ για το απόλυτο άριστα... είτε γεωμετρικά είτε με τον τύπο του εμβαδού, όπως θέλει κανείς
οδηγείται άμεσα σε κλασσικό όριο.. Αλλά νομίζω πραγματικά ότι το κερασάκι στην τούρτα είναι το Δ4... Το Δ4 πρέπει να είναι για το απόλυτο άριστα και ΕΙΝΑΙ για το απόλυτο άριστα... είτε γεωμετρικά είτε με τον τύπο του εμβαδού, όπως θέλει κανείςΔεν σας κουράζω άλλο. Επαναλαμβάνω την προσωπική μου εκτίμηση : ΕΞΑΙΡΕΤΙΚΟ !
ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΟΛΟΨΥΧΑ ΣΕ ΟΛΟΥΣ, ΕΚΠΑΙΔΕΥΤΙΚΟΥΣ ΚΑΙ ΑΓΩΝΙΖΟΜΕΝΗ ΝΕΟΛΑΙΑ !!!
Τους Λαιστρυγόνας και τους Κύκλωπας,
τον άγριο Ποσειδώνα δεν θα συναντήσεις,
αν δεν τους κουβανείς μες την ψυχή σου,
αν η ψυχή σου δεν τους στήνει εμπρός σου
(ΙΘΑΚΗ - Κ.Π. ΚΑΒΑΦΗΣ)
τον άγριο Ποσειδώνα δεν θα συναντήσεις,
αν δεν τους κουβανείς μες την ψυχή σου,
αν η ψυχή σου δεν τους στήνει εμπρός σου
(ΙΘΑΚΗ - Κ.Π. ΚΑΒΑΦΗΣ)
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5561
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: Ενα πολύ καλό διαγώνισμα απο τον Δημήτρη Ντρίζο.
Γεια σας !
Μετά από τόσον καιρό ...αξιώθηκα και γω να λύσω γραμμή-γραμμή και με προσοχή όλα τα ερωτήματα ,προσπαθώντας να δω αν επιτρέπουν δημιουργία διαλόγου με έναν μαθητή, στον οποίο θα τα δώσει κάποιος για λύση.
Τα θέματα είναι προσεγμένα και μερικά ερωτήματα επιδέχονται και άλλες προσεγγίσεις ,κάτι που κάνει το διαγώνισμα ιδιαίτερα χρήσιμο αυτή την περίοδο.
Τα συνευθειακά σημεία (στο Δ) δίνουν την αφορμή να αποδείξει κάποιος ότι μια ευθεία και μια κυρτή συνάρτηση έχουν το πολύ δύο κοινά σημεία.Από την άλλη η παρουσία της σπρώχνει το μαθητή στην αναλυτική γεωμετρία, αφού δηλώνει το συντελεστή διεύθυνσης της ΟΑ κλπ.
σπρώχνει το μαθητή στην αναλυτική γεωμετρία, αφού δηλώνει το συντελεστή διεύθυνσης της ΟΑ κλπ.
Τέτοια ερωτήματα είναι καλά για το μαθητή και δημιουργούνε ωραίο κλίμα για συζήτηση μια και συνδυάζουν γεωμετρία, διαίσθηση και αυστηρή προσέγγιση με ανάλυση .
Αμέσως πιο κάτω το εμβαδόν και το υπαρζιακό ανοίγει νέο διάλογο : να αναζητήσουμε τον τύπο του εμβαδού τριγώνου από την Β Κατ ή να πάμε με τρίγωνα και τραπέζια, μέσω της κλασικής οδού ; ΚΑλό ερώτημα και η λύση πράγματα απαιτεί πολύ καλή προετοιμασία και καλή μαθηματική υποδομή .
Αλλά και η εύρεση των α,β για την ασύμπτωτη στο Β θέλει προσοχή.Εκεί χρειάζεται και μια σχετική διευρεύνηση και ο κανόνες de L'Hospital δεν είναι καθόλου καλή επιλογή γιατί αφήνει ίσως θεωρητικά κενά.Ποιος είναι ο μεγιστοβάθμιος όρος στον αριθμητή ; Για το μαθητή αυτά είναι δύσκολα σημεία που εύκολα τα παραβλεπει, χάνοντας μονάδες.
Προφανώς, δεν χωράνε όλα σε ένα διαγώνισμα.Μπορεί κάτι από το ολοκλήρωμα να φαίνεται απαραίτητο, αλλά αν φορτώσουμε πιο πολύ τα θέματα πάμε στην περίοδο 12-15 με τα γνωστά ζητήματα αλλά και μετέπειτα χρόνια που χαρακτηρίζονται από τον όγκο των θεμάτων.
Δεν θέλω να παινέσω τα θέματα μόνο επειδή τα έχουν συντάξει ...πατριωτάκια Θεσσαλοί και μάλιστα αρκετοί από τον νομό Καρδίτσας, αλλά νομίζω ότι ένα ΕΥΧΑΡΙΣΤΩ από την καρδιά μου και ένα ΕΥΓΕ είναι απαραίτητο προς όλους.
Τα θέματα δείχνουν σεβασμό στο μαθητή, δεν είναι βέβαια εύκολα, αλλά τα κρίνω μόνο από την πλευρά της προετοιμασίας. Αν τα θέματα αυτά , όπως είναι , ήταν θέματα πανελλαδικών εξετάσεων, ίσως έβαζα και άλλα κριτήρια για να τα αξιολογήσω, αλλά για την ώρα μένω με την γλυκειά γεύση ότι τα ευχαριστήθηκα ο ίδιος.Δεν είχα τη χαρά να τα δώσω σε μαθητές, που να τους βρεις αυτό τον καιρό, αλλά νομίζω ότι οι ''καλοί'' θα τα επεξεργάζονταν καλά.
Καλό βράδυ σε όλους !
Μετά από τόσον καιρό ...αξιώθηκα και γω να λύσω γραμμή-γραμμή και με προσοχή όλα τα ερωτήματα ,προσπαθώντας να δω αν επιτρέπουν δημιουργία διαλόγου με έναν μαθητή, στον οποίο θα τα δώσει κάποιος για λύση.
Τα θέματα είναι προσεγμένα και μερικά ερωτήματα επιδέχονται και άλλες προσεγγίσεις ,κάτι που κάνει το διαγώνισμα ιδιαίτερα χρήσιμο αυτή την περίοδο.
Τα συνευθειακά σημεία (στο Δ) δίνουν την αφορμή να αποδείξει κάποιος ότι μια ευθεία και μια κυρτή συνάρτηση έχουν το πολύ δύο κοινά σημεία.Από την άλλη η παρουσία της
 σπρώχνει το μαθητή στην αναλυτική γεωμετρία, αφού δηλώνει το συντελεστή διεύθυνσης της ΟΑ κλπ.
σπρώχνει το μαθητή στην αναλυτική γεωμετρία, αφού δηλώνει το συντελεστή διεύθυνσης της ΟΑ κλπ.Τέτοια ερωτήματα είναι καλά για το μαθητή και δημιουργούνε ωραίο κλίμα για συζήτηση μια και συνδυάζουν γεωμετρία, διαίσθηση και αυστηρή προσέγγιση με ανάλυση .
Αμέσως πιο κάτω το εμβαδόν και το υπαρζιακό ανοίγει νέο διάλογο : να αναζητήσουμε τον τύπο του εμβαδού τριγώνου από την Β Κατ ή να πάμε με τρίγωνα και τραπέζια, μέσω της κλασικής οδού ; ΚΑλό ερώτημα και η λύση πράγματα απαιτεί πολύ καλή προετοιμασία και καλή μαθηματική υποδομή .
Αλλά και η εύρεση των α,β για την ασύμπτωτη στο Β θέλει προσοχή.Εκεί χρειάζεται και μια σχετική διευρεύνηση και ο κανόνες de L'Hospital δεν είναι καθόλου καλή επιλογή γιατί αφήνει ίσως θεωρητικά κενά.Ποιος είναι ο μεγιστοβάθμιος όρος στον αριθμητή ; Για το μαθητή αυτά είναι δύσκολα σημεία που εύκολα τα παραβλεπει, χάνοντας μονάδες.
Προφανώς, δεν χωράνε όλα σε ένα διαγώνισμα.Μπορεί κάτι από το ολοκλήρωμα να φαίνεται απαραίτητο, αλλά αν φορτώσουμε πιο πολύ τα θέματα πάμε στην περίοδο 12-15 με τα γνωστά ζητήματα αλλά και μετέπειτα χρόνια που χαρακτηρίζονται από τον όγκο των θεμάτων.
Δεν θέλω να παινέσω τα θέματα μόνο επειδή τα έχουν συντάξει ...πατριωτάκια Θεσσαλοί και μάλιστα αρκετοί από τον νομό Καρδίτσας, αλλά νομίζω ότι ένα ΕΥΧΑΡΙΣΤΩ από την καρδιά μου και ένα ΕΥΓΕ είναι απαραίτητο προς όλους.
Τα θέματα δείχνουν σεβασμό στο μαθητή, δεν είναι βέβαια εύκολα, αλλά τα κρίνω μόνο από την πλευρά της προετοιμασίας. Αν τα θέματα αυτά , όπως είναι , ήταν θέματα πανελλαδικών εξετάσεων, ίσως έβαζα και άλλα κριτήρια για να τα αξιολογήσω, αλλά για την ώρα μένω με την γλυκειά γεύση ότι τα ευχαριστήθηκα ο ίδιος.Δεν είχα τη χαρά να τα δώσω σε μαθητές, που να τους βρεις αυτό τον καιρό, αλλά νομίζω ότι οι ''καλοί'' θα τα επεξεργάζονταν καλά.
Καλό βράδυ σε όλους !
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες


