Δίνεται η συνεχής συνάρτηση
 . Αν ισχύει
. Αν ισχύει  , να δείξετε ότι υπάρχει ένα τουλάχιστον
, να δείξετε ότι υπάρχει ένα τουλάχιστον ![\xi \epsilon [-\frac{5}{4},-\frac{1}{4}] \xi \epsilon [-\frac{5}{4},-\frac{1}{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/5be28276d492176eb6e4169bf0191af4.png) τέτοιο ώστε
τέτοιο ώστε  και να ερμηνεύσετε γεωμετρικά το αποτέλεσμα.
και να ερμηνεύσετε γεωμετρικά το αποτέλεσμα.Συντονιστής: Καρδαμίτσης Σπύρος
 . Αν ισχύει
. Αν ισχύει  , να δείξετε ότι υπάρχει ένα τουλάχιστον
, να δείξετε ότι υπάρχει ένα τουλάχιστον ![\xi \epsilon [-\frac{5}{4},-\frac{1}{4}] \xi \epsilon [-\frac{5}{4},-\frac{1}{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/5be28276d492176eb6e4169bf0191af4.png) τέτοιο ώστε
τέτοιο ώστε  και να ερμηνεύσετε γεωμετρικά το αποτέλεσμα.
και να ερμηνεύσετε γεωμετρικά το αποτέλεσμα.ΛΥΣΗ
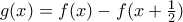 που είναι συνεχής στο
που είναι συνεχής στο  ως πράξεις συνεχών με
ως πράξεις συνεχών με  και
και  και
και  έχουμε με πρόσθεση κατά μέλη ότι
έχουμε με πρόσθεση κατά μέλη ότι  (1)
(1)  για κάθε
για κάθε ![x\in [-\frac{5}{4},\,-\frac{1}{4}] x\in [-\frac{5}{4},\,-\frac{1}{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/bb581bae8fb3c78987463cfdc1497f5e.png) θα έχει σταθερό πρόσημο δηλαδή
θα έχει σταθερό πρόσημο δηλαδή  ή
ή  και από (1) άτοπο
και από (1) άτοπο ![{{x}_{0}}\in [-\frac{5}{4},\,-\frac{1}{4}] {{x}_{0}}\in [-\frac{5}{4},\,-\frac{1}{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/7e982e6059e115328a65f35d18e97c77.png) που
που  ή
ή 
 μήκους
μήκους 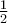
Να σημειώσω ότιKAKABASBASILEIOS έγραψε: ↑Τετ Μάιος 02, 2018 1:08 pmΛΥΣΗ
Θεωρώντας την συνάρτησηπου είναι συνεχής στο
ως πράξεις συνεχών με
και
και
έχουμε με πρόσθεση κατά μέλη ότι
(1)
και ανγια κάθε
θα έχει σταθερό πρόσημο δηλαδή
ή
και από (1) άτοπο
άρα υπάρχειπου
ή

και γεωμετρικά σημαίνει ότι υπάρχει χορδή οριζόντια της γραφικής παράστασης τηςμήκους
...μετά από Π.Μ. του Σταυρου του Παπαδόπουλου διόρθωσα την αβλεψία μου στο διάστημα...
Φιλικά και Μαθηματικά
Βασίλης
 μπορούμε να το έχουμε στο
μπορούμε να το έχουμε στο  .
. συμπεραίνουμε ότι οι αριθμοί
συμπεραίνουμε ότι οι αριθμοί 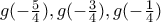 η θα είναι και οι τρεις
η θα είναι και οι τρεις  όποτε π.χ
όποτε π.χ 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες