M.S.Vovos έγραψε: ↑Παρ Απρ 13, 2018 4:01 pm
Έστω η παραγωγίσιμη συνάρτηση

με

τέτοια ώστε, για κάθε

να ισχύει:
 (α)
(α) Να αποδείξετε ότι
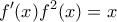
, για κάθε

.
(β) Να αποδείξετε ότι
![\displaystyle f(x)=\sqrt[3]{\frac{3x^{2}}{2}+1} \displaystyle f(x)=\sqrt[3]{\frac{3x^{2}}{2}+1}](/forum/ext/geomar/texintegr/latexrender/pictures/fcace37eb7559f85a67f449cef203b5a.png)
,

.
(γ.i.) Να μελετήσετε την

ως προς:
- τις ασύμπτωτες ευθείες της.
(γ.ii.) Να σχεδιάσετε τη γραφική παράσταση της

.
(δ) Αν
![\displaystyle a,b\in \left [ -\sqrt{2},\sqrt{2} \right ] \displaystyle a,b\in \left [ -\sqrt{2},\sqrt{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/70c1a1f23b1fdafd5cf04b7555d1920a.png)
με άθροισμα

, τότε να βρείτε την ελάχιστη τιμή της παράστασης:
![\displaystyle{\displaystyle \mathcal{A}=\sqrt[3]{3a^{2}+2}+\sqrt[3]{3b^{2}+2}} \displaystyle{\displaystyle \mathcal{A}=\sqrt[3]{3a^{2}+2}+\sqrt[3]{3b^{2}+2}}](/forum/ext/geomar/texintegr/latexrender/pictures/c49c8c1b69fe576b390458459ae5b009.png) Φιλικά,
Φιλικά,
Μάριος
Καλησπέρα.
Μια προσπάθεια στα τρία πρώτα ...
(α) Είναι:
![\dfrac{f^{3}(x+h)-f^{3}(x-h)-6xh}{h}=\dfrac{\left [f(x+h)-f(x-h) \right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]-6xh}{h}= \dfrac{f^{3}(x+h)-f^{3}(x-h)-6xh}{h}=\dfrac{\left [f(x+h)-f(x-h) \right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]-6xh}{h}=](/forum/ext/geomar/texintegr/latexrender/pictures/7851e23e7cf1dc71b56f67775d8014c2.png)
![=\left [\dfrac{f(x+h)-f(x) }{h} - \dfrac{f(x-h)-f(x) }{h}\right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]- 6xh =\left [\dfrac{f(x+h)-f(x) }{h} - \dfrac{f(x-h)-f(x) }{h}\right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]- 6xh](/forum/ext/geomar/texintegr/latexrender/pictures/a6a7708b79493b36aa52dc4b4b6d4e8a.png)
Θέτω

.

.
Γνωρίζουμε ότι η

είναι παραγωγίσιμη στο

.
Άρα

.
Επίσης η

είναι συνεχής στο

, άρα και συνεχής στο

και στο

.
Συνεπώς

.
Θέτοντας

, έχουμε

, οπότε

.
Ομοίως

.
Τελικά έχουμε





.
(β) Ισχύει :





.
Συνεπώς από Πόρισμα Συνεπειών ΘΜΤ συμπεραίνουμε ότι

.
Θέτω

από όπου προκύπτει
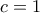
. Επομένως

.
Άρα

,

. Άρα και

,

.
Άρα
![\displaystyle f(x)=\sqrt[3]{\dfrac{3x^{2}}{2}+1} \displaystyle f(x)=\sqrt[3]{\dfrac{3x^{2}}{2}+1}](/forum/ext/geomar/texintegr/latexrender/pictures/5d7015f1a823cbf2145bf0e9e9cd52ab.png)
.
(γ) (i) Είναι

Επομένως
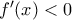
,



: γνησίως φθίνουσα στο
![(-\infty , 0] (-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/d12a2fb16bdbeb159972fe9c68664dc2.png)
.
Επίσης

,



: γνησίως αύξουσα στο

.
Συνεπώς η

παρουσιάζει (ολικό) ελάχιστο στο

, το

.
Θέτοντας

, έχουμε

,
οπότε

. Ομοίως

.
Από την μονοτονία και την συνέχεια της

προκύπτει ότι το σύνολο τιμών της είναι το

.
Επίσης η

είναι παραγωγίσιμη . Συνεπώς έχουμε

.
Επί πλέον η

είναι παραγωγίσιμη . Συνεπώς έχουμε

.
Από τα παραπάνω προκύπτουν :

,



: κοίλη στο
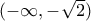
.

,



: κυρτή στο

.

,



: κοίλη στο

.
Επίσης ισχύει

.
Άρα σημεία καμπής τα
![B (-\sqrt{2}, \sqrt[3]{4}) B (-\sqrt{2}, \sqrt[3]{4})](/forum/ext/geomar/texintegr/latexrender/pictures/4e8343fe4db6bfe29cd865e001d4d43a.png)
και
![C (\sqrt{2}, \sqrt[3]{4}) C (\sqrt{2}, \sqrt[3]{4})](/forum/ext/geomar/texintegr/latexrender/pictures/fb8d4a264dab6224aef55bb634081b56.png)
.
Για τις ασύμπτωτες έχουμε :
Κατ' αρχάς η

δεν παρουσιάζει κατακόρυφες ασύπτωτες αφού είναι συνεχής στο

.
Επίσης έχουμε
![\displaystyle{\lim_{x\rightarrow -\infty }\frac{f(x)}{x}= \lim_{x\rightarrow -\infty }\frac{\sqrt[3]{\frac{3x^2}{2}+1}}{-(-x)}} = \lim_{x\rightarrow -\infty }\left (-\sqrt[3]{\frac{3x^2+1}{-2x^3}} \right ) = 0 \displaystyle{\lim_{x\rightarrow -\infty }\frac{f(x)}{x}= \lim_{x\rightarrow -\infty }\frac{\sqrt[3]{\frac{3x^2}{2}+1}}{-(-x)}} = \lim_{x\rightarrow -\infty }\left (-\sqrt[3]{\frac{3x^2+1}{-2x^3}} \right ) = 0](/forum/ext/geomar/texintegr/latexrender/pictures/769292b64c22530143831fee313f12c9.png)
,
αφού το όριο της ρητής συνάρτησης μέσα στη ρίζα είναι μηδέν.
Όμως

.
Άρα η

δεν παρουσιάζει πλάγια ασύμπτωτη στο

.
Ομοίως προκύπτει ότι η

δεν παρουσιάζει πλάγια ασύμπτωτη στο

.
(γ)(ii)

- Επαναληπτική 2_2018.png (8.1 KiB) Προβλήθηκε 1063 φορές
Φιλικά
Σταμ. Γλάρος
 με
με  τέτοια ώστε, για κάθε
τέτοια ώστε, για κάθε  να ισχύει:
να ισχύει:
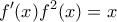 , για κάθε
, για κάθε  .
.![\displaystyle f(x)=\sqrt[3]{\frac{3x^{2}}{2}+1} \displaystyle f(x)=\sqrt[3]{\frac{3x^{2}}{2}+1}](/forum/ext/geomar/texintegr/latexrender/pictures/fcace37eb7559f85a67f449cef203b5a.png) ,
,  .
. ως προς:
ως προς:
 .
.![\displaystyle a,b\in \left [ -\sqrt{2},\sqrt{2} \right ] \displaystyle a,b\in \left [ -\sqrt{2},\sqrt{2} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/70c1a1f23b1fdafd5cf04b7555d1920a.png) με άθροισμα
με άθροισμα  , τότε να βρείτε την ελάχιστη τιμή της παράστασης:
, τότε να βρείτε την ελάχιστη τιμή της παράστασης: ![\displaystyle{\displaystyle \mathcal{A}=\sqrt[3]{3a^{2}+2}+\sqrt[3]{3b^{2}+2}} \displaystyle{\displaystyle \mathcal{A}=\sqrt[3]{3a^{2}+2}+\sqrt[3]{3b^{2}+2}}](/forum/ext/geomar/texintegr/latexrender/pictures/c49c8c1b69fe576b390458459ae5b009.png)

![\dfrac{f^{3}(x+h)-f^{3}(x-h)-6xh}{h}=\dfrac{\left [f(x+h)-f(x-h) \right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]-6xh}{h}= \dfrac{f^{3}(x+h)-f^{3}(x-h)-6xh}{h}=\dfrac{\left [f(x+h)-f(x-h) \right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]-6xh}{h}=](/forum/ext/geomar/texintegr/latexrender/pictures/7851e23e7cf1dc71b56f67775d8014c2.png)
![=\left [\dfrac{f(x+h)-f(x) }{h} - \dfrac{f(x-h)-f(x) }{h}\right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]- 6xh =\left [\dfrac{f(x+h)-f(x) }{h} - \dfrac{f(x-h)-f(x) }{h}\right ]\left [ f^2(x+h)+f(x+h)f(x-h)+f^2(x-h) \right ]- 6xh](/forum/ext/geomar/texintegr/latexrender/pictures/a6a7708b79493b36aa52dc4b4b6d4e8a.png)
 .
.  .
. .
. .
. και στο
και στο  .
. .
. , έχουμε
, έχουμε  , οπότε
, οπότε  .
. .
.

 .
.
 .
. .
. από όπου προκύπτει
από όπου προκύπτει 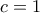 . Επομένως
. Επομένως  .
. ,
,  . Άρα και
. Άρα και  ,
, ![\displaystyle f(x)=\sqrt[3]{\dfrac{3x^{2}}{2}+1} \displaystyle f(x)=\sqrt[3]{\dfrac{3x^{2}}{2}+1}](/forum/ext/geomar/texintegr/latexrender/pictures/5d7015f1a823cbf2145bf0e9e9cd52ab.png) .
.
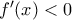 ,
, 

 : γνησίως φθίνουσα στο
: γνησίως φθίνουσα στο ![(-\infty , 0] (-\infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/d12a2fb16bdbeb159972fe9c68664dc2.png) .
. ,
, 
 .
. , έχουμε
, έχουμε  ,
, . Ομοίως
. Ομοίως  .
.  .
. .
. είναι παραγωγίσιμη . Συνεπώς έχουμε
είναι παραγωγίσιμη . Συνεπώς έχουμε  .
. ,
, 
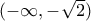 .
. ,
, 
 .
.
 .
. .
.![B (-\sqrt{2}, \sqrt[3]{4}) B (-\sqrt{2}, \sqrt[3]{4})](/forum/ext/geomar/texintegr/latexrender/pictures/4e8343fe4db6bfe29cd865e001d4d43a.png) και
και ![C (\sqrt{2}, \sqrt[3]{4}) C (\sqrt{2}, \sqrt[3]{4})](/forum/ext/geomar/texintegr/latexrender/pictures/fb8d4a264dab6224aef55bb634081b56.png) .
.![\displaystyle{\lim_{x\rightarrow -\infty }\frac{f(x)}{x}= \lim_{x\rightarrow -\infty }\frac{\sqrt[3]{\frac{3x^2}{2}+1}}{-(-x)}} = \lim_{x\rightarrow -\infty }\left (-\sqrt[3]{\frac{3x^2+1}{-2x^3}} \right ) = 0 \displaystyle{\lim_{x\rightarrow -\infty }\frac{f(x)}{x}= \lim_{x\rightarrow -\infty }\frac{\sqrt[3]{\frac{3x^2}{2}+1}}{-(-x)}} = \lim_{x\rightarrow -\infty }\left (-\sqrt[3]{\frac{3x^2+1}{-2x^3}} \right ) = 0](/forum/ext/geomar/texintegr/latexrender/pictures/769292b64c22530143831fee313f12c9.png) ,
, .
. .
.![a,b\in [-\sqrt{2},\sqrt{2}] a,b\in [-\sqrt{2},\sqrt{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/4075516b16000ac45a6518e5b3f6bbd2.png) ισχύει:
ισχύει:
 είναι η
είναι η  αφού επιτυγχάνεται για
αφού επιτυγχάνεται για 