
 Να εξετάσετε αν η
Να εξετάσετε αν η  είναι συνεχής, στο
είναι συνεχής, στο 
 Να βρείτε τα διαστήματα μονοτονίας και τα ακρότατα της
Να βρείτε τα διαστήματα μονοτονίας και τα ακρότατα της 
 Να βρείτε το σύνολο τιμών της
Να βρείτε το σύνολο τιμών της 
 Να εξετάσετε τη συνάρτηση
Να εξετάσετε τη συνάρτηση  ως προς την κυρτότητα και να βρείτε τα σημεία καμπής.
ως προς την κυρτότητα και να βρείτε τα σημεία καμπής. Να σχεδιάσετε τη γραφική παράσταση της
Να σχεδιάσετε τη γραφική παράσταση της 
 Να δείξετε ότι
Να δείξετε ότι 
 Να υπολογίσετε το εμβαδόν
Να υπολογίσετε το εμβαδόν  του χωρίου που περικλείεται από τη γραφική παράσταση της
του χωρίου που περικλείεται από τη γραφική παράσταση της 
την ασύμπτωτή της στο
 τον άξονα
τον άξονα 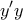 και την ευθεία
και την ευθεία 
 Να υπολογίσετε το όριο
Να υπολογίσετε το όριο 

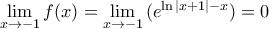 γιατί
γιατί 
 η
η  παραγωγίσιμη η
παραγωγίσιμη η  και
και  και
και 
![[-1,\,0] [-1,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/939d27e75a23bf6cf35057dfbfb460b9.png) και
και 
![(-\infty ,\,-1],\,\,[0,\,+\infty ) (-\infty ,\,-1],\,\,[0,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/7c1a5c65330737e73092f362b41ac1d2.png) επομένως παρουσιάζει τοπικό ελάχιστο
επομένως παρουσιάζει τοπικό ελάχιστο  (που είναι και ολικό αφού
(που είναι και ολικό αφού  ) και τοπικό μέγιστο το
) και τοπικό μέγιστο το 
 και
και  γιατί
γιατί 
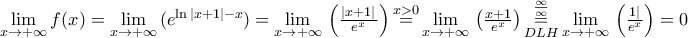

 παραγωγίσιμη με
παραγωγίσιμη με 
 με
με  και
και  άρα η
άρα η ![(-\infty ,\,\,-1],\,\,[1,\,\,+\infty ) (-\infty ,\,\,-1],\,\,[1,\,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/b3ac6da03889fd65b350598fd22860af.png) και
και 
![[-1,\,1] [-1,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/75b6db3096497c8b4d1a5e75331a4335.png) άρα έχει σημείο καμπής το
άρα έχει σημείο καμπής το  ή
ή 
 και ολοκληρώνοντας έχουμε
και ολοκληρώνοντας έχουμε 

![=-\left[ (x+1){{e}^{-x}} \right]_{0}^{a}+\int\limits_{0}^{a}{{{e}^{-x}}dx}=-\left[ (x+1){{e}^{-x}} \right]_{0}^{a}-\left[ {{e}^{-x}} \right]_{0}^{a}=-\left[ (x+2){{e}^{-x}} \right]_{0}^{a} =-\left[ (x+1){{e}^{-x}} \right]_{0}^{a}+\int\limits_{0}^{a}{{{e}^{-x}}dx}=-\left[ (x+1){{e}^{-x}} \right]_{0}^{a}-\left[ {{e}^{-x}} \right]_{0}^{a}=-\left[ (x+2){{e}^{-x}} \right]_{0}^{a}](/forum/ext/geomar/texintegr/latexrender/pictures/fe0f099f6f4a9a18270cee28206470ef.png) άρα
άρα ![E(a)=-\left[ (x+2){{e}^{-x}} \right]_{0}^{a}=2-\frac{a+2}{{{e}^{a}}} E(a)=-\left[ (x+2){{e}^{-x}} \right]_{0}^{a}=2-\frac{a+2}{{{e}^{a}}}](/forum/ext/geomar/texintegr/latexrender/pictures/90c88588b03ae87571e3eef8508a7db6.png)
 επειδή
επειδή 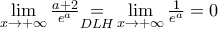
![\displaystyle \begin{array}{l}
\int\limits_0^1 {{e^{\ln |x + 1| - x}}} \,dx\mathop = \limits^{|x + 1| = x + 1} \int\limits_0^1 {{e^{\ln \left( {x + 1} \right)}}{e^{ - x}}} \,dx = \int\limits_0^1 {\left( {x + 1} \right){e^{ - x}}} \,dx = \left[ { - \left( {x + 2} \right){e^{ - x}}} \right]_0^1 = ... = \frac{{2e - 3}}{e}\\
\\
\frac{2}{e} \le \frac{{2e - 3}}{e} \le 1 \Leftrightarrow 2 \le 2e - 3 \le e \Leftrightarrow 5 \le 2e \le e + 3
\end{array} \displaystyle \begin{array}{l}
\int\limits_0^1 {{e^{\ln |x + 1| - x}}} \,dx\mathop = \limits^{|x + 1| = x + 1} \int\limits_0^1 {{e^{\ln \left( {x + 1} \right)}}{e^{ - x}}} \,dx = \int\limits_0^1 {\left( {x + 1} \right){e^{ - x}}} \,dx = \left[ { - \left( {x + 2} \right){e^{ - x}}} \right]_0^1 = ... = \frac{{2e - 3}}{e}\\
\\
\frac{2}{e} \le \frac{{2e - 3}}{e} \le 1 \Leftrightarrow 2 \le 2e - 3 \le e \Leftrightarrow 5 \le 2e \le e + 3
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/1645cf342bfbe1e3f26cb99340fd615c.png)
 , εντούτοις, νομίζω ότι, στο (4), δηλαδή στην εύρεση των σημείων καμπής πρέπει να δικαιολογήσουμε γιατί απορρίπτουμε το
, εντούτοις, νομίζω ότι, στο (4), δηλαδή στην εύρεση των σημείων καμπής πρέπει να δικαιολογήσουμε γιατί απορρίπτουμε το  .
. είναι
είναι  .
. είναι
είναι  .
. , είναι διαφορετικά, η
, είναι διαφορετικά, η  , οπότε στο σημείο αυτό δεν ορίζεται εφαπτομένη της, άρα το
, οπότε στο σημείο αυτό δεν ορίζεται εφαπτομένη της, άρα το