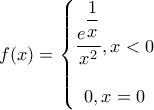
1) Να αποδείξετε οτι είναι συνεχής
2) Να υπολογίσετε το

3) Να υπολογίσετε το
![\displaystyle{\lim_{x \to -\infty}\left [ F(x)-F(x-1) \right ]} \displaystyle{\lim_{x \to -\infty}\left [ F(x)-F(x-1) \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/dad8599e78abba768371c4ba8d57c599.png) , όπου
, όπου  μια αρχική της
μια αρχική της 
4) Να δειχθεί οτι η εξίσωση
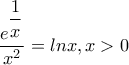 έχει μοναδική ρίζα στο διάστημα
έχει μοναδική ρίζα στο διάστημα 
Συντονιστής: Καρδαμίτσης Σπύρος
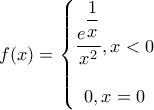

![\displaystyle{\lim_{x \to -\infty}\left [ F(x)-F(x-1) \right ]} \displaystyle{\lim_{x \to -\infty}\left [ F(x)-F(x-1) \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/dad8599e78abba768371c4ba8d57c599.png) , όπου
, όπου  μια αρχική της
μια αρχική της 
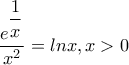 έχει μοναδική ρίζα στο διάστημα
έχει μοναδική ρίζα στο διάστημα 
Στοerxmer έγραψε:Δίνεται η συνάρτηση με τύπο
1) Να αποδείξετε οτι είναι συνεχής
2) Να υπολογίσετε το
3) Να υπολογίσετε το, όπου
μια αρχική της

4) Να δειχθεί οτι η εξίσωσηέχει μοναδική ρίζα στο διάστημα
 δεν είναι ορισμένη η συνάρτηση.Πως θα δείξουμε ότι έχει ρίζα.
δεν είναι ορισμένη η συνάρτηση.Πως θα δείξουμε ότι έχει ρίζα....για τα δύο πρώτα ερωτήματα....erxmer έγραψε:Δίνεται η συνάρτηση με τύπο
1) Να αποδείξετε οτι είναι συνεχής
2) Να υπολογίσετε το
3) Να υπολογίσετε το, όπου
μια αρχική της

4) Να δειχθεί οτι η εξίσωσηέχει μοναδική ρίζα στο διάστημα
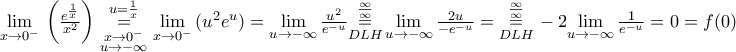
 είναι συνεχής στο
είναι συνεχής στο  και επειδή είναι συνεχής στο
και επειδή είναι συνεχής στο  ως πράξεις συνεχών είναι συνεχής στο
ως πράξεις συνεχών είναι συνεχής στο 
 είναι μία αρχική της
είναι μία αρχική της  στο
στο  θα έχει την μορφή
θα έχει την μορφή  αυτή θα είναι συνεχής άρα
αυτή θα είναι συνεχής άρα 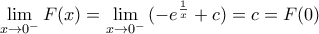
 και πρέπει
και πρέπει 

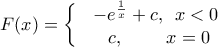 και
και 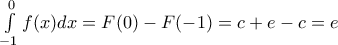
![\displaystyle{\lim_{x \to -\infty}\left [ F(x)-F(x-1) \right ]} \displaystyle{\lim_{x \to -\infty}\left [ F(x)-F(x-1) \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/dad8599e78abba768371c4ba8d57c599.png) επειδή
επειδή ![\underset{x\to -\infty }{\mathop{\lim }}\,\left[ F(x)) \right]=\underset{x\to -\infty }{\mathop{\lim }}\,\left( {{e}^{-\frac{1}{x}}}+c \right)\underset{\begin{smallmatrix}
x\to -\infty \\
u\to 0
\end{smallmatrix}}{\overset{u=-\frac{1}{x}}{\mathop{=}}}\,\underset{u\to 0}{\mathop{\lim }}\,\left( {{e}^{u}}+c \right)=1+c \underset{x\to -\infty }{\mathop{\lim }}\,\left[ F(x)) \right]=\underset{x\to -\infty }{\mathop{\lim }}\,\left( {{e}^{-\frac{1}{x}}}+c \right)\underset{\begin{smallmatrix}
x\to -\infty \\
u\to 0
\end{smallmatrix}}{\overset{u=-\frac{1}{x}}{\mathop{=}}}\,\underset{u\to 0}{\mathop{\lim }}\,\left( {{e}^{u}}+c \right)=1+c](/forum/ext/geomar/texintegr/latexrender/pictures/bf8bb5727fc2e7516582765ddb28cdb0.png) και
και ![\underset{x\to -\infty }{\mathop{\lim }}\,\left[ F(x-1) \right]\underset{\begin{smallmatrix}
x\to -\infty \\
u\to -\infty
\end{smallmatrix}}{\overset{u=x-1}{\mathop{=}}}\,\underset{u\to -\infty }{\mathop{\lim }}\,F(u)=1+c \underset{x\to -\infty }{\mathop{\lim }}\,\left[ F(x-1) \right]\underset{\begin{smallmatrix}
x\to -\infty \\
u\to -\infty
\end{smallmatrix}}{\overset{u=x-1}{\mathop{=}}}\,\underset{u\to -\infty }{\mathop{\lim }}\,F(u)=1+c](/forum/ext/geomar/texintegr/latexrender/pictures/e70f8cfb878d1da78bdd94070d2ddea0.png) το
το ![\underset{x\to -\infty }{\mathop{\lim }}\,\left[ F(x)-F(x-1) \right]=0 \underset{x\to -\infty }{\mathop{\lim }}\,\left[ F(x)-F(x-1) \right]=0](/forum/ext/geomar/texintegr/latexrender/pictures/b010300fc0a152473106eef37ca3f930.png)
Κάνω το 4) για να κλείσειerxmer έγραψε:Δίνεται η συνάρτηση με τύπο
1) Να αποδείξετε οτι είναι συνεχής
2) Να υπολογίσετε το
3) Να υπολογίσετε το, όπου
μια αρχική της

4) Να δειχθεί οτι η εξίσωσηέχει μοναδική ρίζα στο διάστημα




Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες