
 σταθερός.
σταθερός.1) Να δείξετε ότι η
 είναι γνησίως αύξουσα και κοίλη στο
είναι γνησίως αύξουσα και κοίλη στο 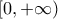 .
.2) Να ϐρείτε το εµβαδόν του χωρίου που περικλείετε από τη
 , τον άξονα
, τον άξονα 
και τις ευθείες

3) Να ϐρείτε
 ώστε η ευθεία
ώστε η ευθεία  να χωρίζει το ανωτέρω χωρίο σε δύο ισεµβαδικά μέρη
να χωρίζει το ανωτέρω χωρίο σε δύο ισεµβαδικά μέρη 4) Aν
 να υπολογιστεί το όριο
να υπολογιστεί το όριο 
ερωτήμα bonus αν το
 υπάρχει τρόπος να βρεθεί σε πιο γενική μορφή το παραπάνω όριο;
υπάρχει τρόπος να βρεθεί σε πιο γενική μορφή το παραπάνω όριο;

 (σχολικό εφαρμογή)
(σχολικό εφαρμογή)



 για κάθε
για κάθε  και αφού είναι συνεχής στο
και αφού είναι συνεχής στο  για κάθε
για κάθε  άρα κοίλη στο
άρα κοίλη στο ![E=\int\limits_{0}^{2}{|f(x)|dx}=\int\limits_{0}^{2}{{{x}^{a}}dx}=\frac{1}{a+1}\left[ {{x}^{a+1}} \right]_{0}^{2}=\frac{1}{a+1}\left( {{2}^{a+1}}-0 \right)=\frac{1}{a+1}{{2}^{a+1}} E=\int\limits_{0}^{2}{|f(x)|dx}=\int\limits_{0}^{2}{{{x}^{a}}dx}=\frac{1}{a+1}\left[ {{x}^{a+1}} \right]_{0}^{2}=\frac{1}{a+1}\left( {{2}^{a+1}}-0 \right)=\frac{1}{a+1}{{2}^{a+1}}](/forum/ext/geomar/texintegr/latexrender/pictures/8ec247aeac39df8396fe15e6779191b1.png)
![\int\limits_{0}^{t}{{{x}^{a}}dx}=\frac{E}{2}\Leftrightarrow \left[ {{x}^{a+1}} \right]_{0}^{t}=\frac{{{2}^{a}}}{a+1}\Leftrightarrow {{t}^{a+1}}=\frac{{{2}^{a}}}{a+1} \int\limits_{0}^{t}{{{x}^{a}}dx}=\frac{E}{2}\Leftrightarrow \left[ {{x}^{a+1}} \right]_{0}^{t}=\frac{{{2}^{a}}}{a+1}\Leftrightarrow {{t}^{a+1}}=\frac{{{2}^{a}}}{a+1}](/forum/ext/geomar/texintegr/latexrender/pictures/2c9df740580c0cbbbd951e8dc12044c2.png) επομένως ισοδύναμα
επομένως ισοδύναμα 

 και αν
και αν  έχουμε
έχουμε 


 επομένως
επομένως 