 ώστε
ώστε . Αν
. Αν  μια αρχική της
μια αρχική της  ώστε
ώστε  .
.1) Nα βρεθεί ο τύπος της συνάρτησης
2) Να μελετηθεί ως προς την μονοτονία
3) Αν
 συνεχής συνάρτηση με
συνεχής συνάρτηση με  και
και  μια αρχική της
μια αρχική της  ώστε
ώστε  . Να λυθεί η ανίσωση
. Να λυθεί η ανίσωση 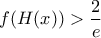
Συντονιστής: Καρδαμίτσης Σπύρος







 είναι το
είναι το  , ισχύει
, ισχύει  για κάθε
για κάθε  . Όμως, η
. Όμως, η  είναι συνεχής, άρα διατηρεί σταθερό πρόσημο στο
είναι συνεχής, άρα διατηρεί σταθερό πρόσημο στο  . Έχουμε όμως
. Έχουμε όμως  , αφού η
, αφού η  είναι γνησίως αύξουσα. Άρα, είναι
είναι γνησίως αύξουσα. Άρα, είναι  για κάθε
για κάθε  και επειδή η
και επειδή η  είναι μια αρχική της
είναι μια αρχική της  ισχύει
ισχύει  για κάθε
για κάθε  , οπότε η
, οπότε η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  . Έτσι, έχουμε:
. Έτσι, έχουμε: .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες