Για τους μαθητές της Γ Λυκείου
Συντονιστής: Καρδαμίτσης Σπύρος
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1739
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Για τους μαθητές της Γ Λυκείου
Δεχόμαστε χωρίς απόδειξη τοRempeskes έγραψε: Ασκηση 21
.......................
Έστω
Τότε, η
Στοισχύει ότι ,
.
 ;
;Kαλαθάκης Γιώργης
- Tolaso J Kos
- Δημοσιεύσεις: 5225
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Για τους μαθητές της Γ Λυκείου
Είχα ξεχάσει ότι η ΕΜΕ έχει πολύ ωραίες ασκήσεις. Για να δούμε:Λάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 20 ΕΜΕ 2012
Εστω η παραγωγίσιμη συνάρτησημε συνεχή παράγωγο, που ικανοποιεί τις σχέσεις :
•, για κάθε
(1)
•(2)
•(3)
Α) Να αποδείξετε ότι,
Β) Να αποδείξετε ότιγια κάθε
Γ) Να μελετήσετε τη συνάρτησηως προς τη μονοτονία και την κυρτότητα
Δ) Αν,
, τότε :
... i) Να αποδείξετε ότι,
... ii) Να βρείτε το εμβαδόν του χωρίου που περικλείεται από τη, τον άξονα
και τις ευθείες με εξισώσεις
και
... iii) Να αποδείξετε ότι, για κάθε
Α) Η δοσμένη σχέση δίδει:

Τώρα, παρατηρούμε ότι στο
 ισχύει
ισχύει  συνεπώς
συνεπώς  και άρα
και άρα  . Οπότε η
. Οπότε η  ως συνεχής, θα διατηρεί και πρόσημο. Για
ως συνεχής, θα διατηρεί και πρόσημο. Για 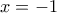 έχουμε ότι
έχουμε ότι  από τη σχέση
από τη σχέση  . Οπότε:
. Οπότε:
Παρόμοια, βγάζουμε και τη σχέση
 . Για
. Για  από τη σχέση
από τη σχέση  έχουμε
έχουμε  . Οπότε:
. Οπότε:
Β) Είναι διαδοχικά:

και το ζητούμενο έπεται.
Γ) Η
 είναι παραγωγίσιμη με παράγωγο
είναι παραγωγίσιμη με παράγωγο  συνεπώς είναι γνήσια αύξουσα. Ναι, αλλά και η
συνεπώς είναι γνήσια αύξουσα. Ναι, αλλά και η  είναι ξανά παραγωγίσιμη με παράγωγο:
είναι ξανά παραγωγίσιμη με παράγωγο:
Συνεπώς η
 είναι κυρτή.
είναι κυρτή.Δ.
α) Η συνάρτηση
 έχει τύπο
έχει τύπο  . Είναι παραγωγίσιμη με παράγωγο:
. Είναι παραγωγίσιμη με παράγωγο:  (απλές πραξούλες).
(απλές πραξούλες). Σημείωση: Από το ερώτημα Γ) έχουμε ότι

Είναι ένας άλλος τρόπος για να βγει η παράγωγος.
β) Εφόσον η
 είναι θετική για το εμβαδόν έχουμε διαδοχικά:
είναι θετική για το εμβαδόν έχουμε διαδοχικά:![\displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1}f(x)\, {\rm d}x\\
&= \int_{0}^{1}\left ( x+ \sqrt{x^2+1} \right )\, {\rm d}x\\
&=\frac{1}{2}+ \int_{0}^{1}\sqrt{x^2+1} \, {\rm d}x \\
&= \frac{1}{2}+ \left [ x \sqrt{x^2+1} \right ]_0^1 - \int_{0}^{1}\frac{x^2}{\sqrt{x^2+1}}\, {\rm d}x\\
&= \frac{1}{2}+ \sqrt{2} - \int_{0}^{1}\frac{x^2+1-1}{\sqrt{x^2+1}}\, {\rm d}x\\
&= \frac{1}{2} + \sqrt{2} - \int_{0}^{1}\frac{x^2+1}{\sqrt{x^2+1}}\, {\rm d}x + \int_{0}^{1}\frac{{\rm d}x}{\sqrt{x^2+1}} \\
&= \frac{1}{2} + \sqrt{2} - \int_{0}^{1}\frac{x^2+1}{\sqrt{x^2+1}} \, {\rm d}x + \left [ \ln \left ( x+\sqrt{x^2+1} \right ) \right ]_0^1 \\
&=\frac{1}{2} + \sqrt{2} - \int_{0}^{1}\frac{x^2+1}{\sqrt{x^2+1}} \, {\rm d}x + \ln \left(1 +\sqrt{2} \right) \\
&=\frac{1}{2}+ \sqrt{2} - \int_{0}^{1}\sqrt{x^2+1}\, {\rm d}x + \ln \left ( 1+\sqrt{2} \right )
\end{aligned}} \displaystyle{\begin{aligned}
{\rm E}\left ( \Omega \right ) &= \int_{0}^{1}f(x)\, {\rm d}x\\
&= \int_{0}^{1}\left ( x+ \sqrt{x^2+1} \right )\, {\rm d}x\\
&=\frac{1}{2}+ \int_{0}^{1}\sqrt{x^2+1} \, {\rm d}x \\
&= \frac{1}{2}+ \left [ x \sqrt{x^2+1} \right ]_0^1 - \int_{0}^{1}\frac{x^2}{\sqrt{x^2+1}}\, {\rm d}x\\
&= \frac{1}{2}+ \sqrt{2} - \int_{0}^{1}\frac{x^2+1-1}{\sqrt{x^2+1}}\, {\rm d}x\\
&= \frac{1}{2} + \sqrt{2} - \int_{0}^{1}\frac{x^2+1}{\sqrt{x^2+1}}\, {\rm d}x + \int_{0}^{1}\frac{{\rm d}x}{\sqrt{x^2+1}} \\
&= \frac{1}{2} + \sqrt{2} - \int_{0}^{1}\frac{x^2+1}{\sqrt{x^2+1}} \, {\rm d}x + \left [ \ln \left ( x+\sqrt{x^2+1} \right ) \right ]_0^1 \\
&=\frac{1}{2} + \sqrt{2} - \int_{0}^{1}\frac{x^2+1}{\sqrt{x^2+1}} \, {\rm d}x + \ln \left(1 +\sqrt{2} \right) \\
&=\frac{1}{2}+ \sqrt{2} - \int_{0}^{1}\sqrt{x^2+1}\, {\rm d}x + \ln \left ( 1+\sqrt{2} \right )
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/035c3f05e8d6cd87bbcfdf32784dde9e.png)
Οπότε αν
 δηλώνει το ολοκλήρωμα
δηλώνει το ολοκλήρωμα  από τη παραπάνω διαδικασία είδαμε ότι:
από τη παραπάνω διαδικασία είδαμε ότι:
Τελικά το ζητούμενο εμβαδόν ισούται με
 .
.γ) Έστω
 η συνάρτηση
η συνάρτηση  . Παρατηρούμε ότι η
. Παρατηρούμε ότι η  είναι παραγωγίσιμη και η παράγωγός της δεν είναι καμία άλλη συνάρτηση παρά η
είναι παραγωγίσιμη και η παράγωγός της δεν είναι καμία άλλη συνάρτηση παρά η  . Όπως είδαμε η
. Όπως είδαμε η  είναι γνήσια αύξουσα αφού
είναι γνήσια αύξουσα αφού  . Όμως για
. Όμως για  είναι
είναι  . Οπότε η
. Οπότε η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  . Άρα στο
. Άρα στο  είναι
είναι  και το συμπέρασμα έπεται.
και το συμπέρασμα έπεται.Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Για τους μαθητές της Γ Λυκείου
ΑΣΚΗΣΗ 9
1) Το όριο γίνεται
 , σχέση (1)
, σχέση (1)
2)απο το (1)![(e^{x}f(x))'=[(2x-3)\cfrac{e^{2x}}{2}-\cfrac{e^{2x}}{2}+2+x]' (e^{x}f(x))'=[(2x-3)\cfrac{e^{2x}}{2}-\cfrac{e^{2x}}{2}+2+x]'](/forum/ext/geomar/texintegr/latexrender/pictures/764b09f088e1446958d44340b7d36320.png)
απο συνέπειες η ζητουμένη
3) kai
kai
 αρα είναι
αρα είναι
κοίλη για χ<0 και κυρτ'η για χ>0 με σημείο καμπής στο 0.
Τ΄ωρα η , γνησίως φθίνουσα για χ<0 και γνησίως αύξουσα για χ>0, με ελάχιστο
, γνησίως φθίνουσα για χ<0 και γνησίως αύξουσα για χ>0, με ελάχιστο
στο ο με τιμή,
συνεπώς απο το πεδίο τιμών της f' έχει μοναδικές ρίζες
4)Τώρα επειδή η συνάρτηση είναι είναι περιττη
είναι περιττη 
αρα
φιλικά dennys
1) Το όριο γίνεται

 , σχέση (1)
, σχέση (1)2)απο το (1)
![(e^{x}f(x))'=[(2x-3)\cfrac{e^{2x}}{2}-\cfrac{e^{2x}}{2}+2+x]' (e^{x}f(x))'=[(2x-3)\cfrac{e^{2x}}{2}-\cfrac{e^{2x}}{2}+2+x]'](/forum/ext/geomar/texintegr/latexrender/pictures/764b09f088e1446958d44340b7d36320.png)
απο συνέπειες η ζητουμένη
3)
 kai
kai  αρα είναι
αρα είναι κοίλη για χ<0 και κυρτ'η για χ>0 με σημείο καμπής στο 0.
Τ΄ωρα η
 , γνησίως φθίνουσα για χ<0 και γνησίως αύξουσα για χ>0, με ελάχιστο
, γνησίως φθίνουσα για χ<0 και γνησίως αύξουσα για χ>0, με ελάχιστο στο ο με τιμή,

συνεπώς απο το πεδίο τιμών της f' έχει μοναδικές ρίζες

4)Τώρα επειδή η συνάρτηση είναι
 είναι περιττη
είναι περιττη 
αρα

φιλικά dennys
Dennys =Ξεκλείδωμα κάθε άσκησης
Re: Για τους μαθητές της Γ Λυκείου
Tolaso J Kos έγραψε:Άσκηση 19
Δίδεται η συνάρτησηη οποία είναι συνεχής στο
και
. Αν ισχύει ότι
και
καθώς επίσης και η σχέση
τότε
- Να δείξετε ότι
.
- Να δείξετε ότι υπάρχει τουλάχιστον ένα
τέτοιο ώστε
.
- Να δείξετε ότι η
δεν είναι
.
- Αν η
γνησίως αύξουσα στο
και
τότε να δείξετε ότι υπάρχει μοναδικό
τέτοιο ώστε
.
 Έστω η συνάρτηση
Έστω η συνάρτηση  η οποία είναι συνεχής ως διαφορά συνεχών συναρτήσεων.
η οποία είναι συνεχής ως διαφορά συνεχών συναρτήσεων.Η
 συνεχής στο
συνεχής στο ![[2008,2009]\subseteq R [2008,2009]\subseteq R](/forum/ext/geomar/texintegr/latexrender/pictures/e5ce1300d1440a7376a3b01624b74bff.png) και ισχύει
και ισχύει  .
.Τότε σύμφωνα από Θεώρημα
 θα υπάρχει ένα τουλάχιστον
θα υπάρχει ένα τουλάχιστον  .
.Όπου
 το
το  στην δοθείσα σχέση και προκύπτει το ζητούμενο.
στην δοθείσα σχέση και προκύπτει το ζητούμενο. Έστω η συνάρτηση
Έστω η συνάρτηση  η οποία είναι συνεχής ως διαφορά συνεχών συναρτήσεων.
η οποία είναι συνεχής ως διαφορά συνεχών συναρτήσεων.Η
 συνεχής στο
συνεχής στο ![[2,3] [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/d5138fec13c27bb6c645b29cdfa97a84.png) με
με ![h(2)h(3)=-f(2)f(3)[f(2)-f(3)]^{2}\leq 0 h(2)h(3)=-f(2)f(3)[f(2)-f(3)]^{2}\leq 0](/forum/ext/geomar/texintegr/latexrender/pictures/e06edf7cf2b87322bfc453468c17ae2d.png) αφού η
αφού η  συνεχής, διάφορη από το μηδέν, άρα διατηρεί πρόσημο και αφού
συνεχής, διάφορη από το μηδέν, άρα διατηρεί πρόσημο και αφού  , τότε
, τότε  .
.Αν
 τότε το
τότε το  ή
ή  .
.Αν
 τότε από Θ.Β. θα υπάρχει ένα
τότε από Θ.Β. θα υπάρχει ένα  .
.Άρα σε κάθε περίπτωση θα υπάρχει ένα
![\rho \in [2,3] \rho \in [2,3]](/forum/ext/geomar/texintegr/latexrender/pictures/00940d07b2d57a9709bc60562c9578fc.png) τέτοιο ώστε
τέτοιο ώστε  .
. Έστω η συνάρτηση
Έστω η συνάρτηση  .Αποδεικνύεται ομοίως ότι υπάρχει ένα τουλάχιστον
.Αποδεικνύεται ομοίως ότι υπάρχει ένα τουλάχιστον ![\xi \in [4,5] \xi \in [4,5]](/forum/ext/geomar/texintegr/latexrender/pictures/e73a53a0828908b53d9d1c9d4265a702.png) τέτοιο ώστε
τέτοιο ώστε  .
. αφού
αφού  .Δηλαδή είναι
.Δηλαδή είναι  . Άρα η
. Άρα η  δεν είναι
δεν είναι  ,
, Είναι
Είναι  , όμοια
, όμοια  .
.Με πρόσθεση κατά μέλη προκύπτει :
 .
.Έστω τώρα η συνάρτηση
 , η οποία ικανοποιεί τις προϋποθέσεις του θεωρήματος
, η οποία ικανοποιεί τις προϋποθέσεις του θεωρήματος  .
.Άρα θα υπάρχει ένα
 (έχω βρει
(έχω βρει  νωρίτερα) τέτοιο ώστε
νωρίτερα) τέτοιο ώστε  και επειδή η
και επειδή η  είναι γνησίως αύξουσα τότε θα είναι και μοναδικό.
είναι γνησίως αύξουσα τότε θα είναι και μοναδικό.- Λάμπρος Μπαλός
- Δημοσιεύσεις: 984
- Εγγραφή: Τρί Αύγ 13, 2013 12:21 pm
- Τοποθεσία: Τρίκαλα
Re: Για τους μαθητές της Γ Λυκείου
Από Εκδόσεις Κανδύλας, μία άσκηση από τα Διαγωνίσματα εφ' όλης της ύλης που μου άρεσε
ΑΣΚΗΣΗ 22 (Τηλέγραφος-Παντούλας)
Δίνονται οι συναρτήσεις με
με  ,
,  .
.
Αν , η
, η  παρουσιάζει ολικό ακρότατο μόνο στη θέση
παρουσιάζει ολικό ακρότατο μόνο στη θέση  το
το  και ισχύει
και ισχύει
 για κάθε
για κάθε  , τότε :
, τότε :
α) να δείξετε ότι , για κάθε
, για κάθε 
β) να δείξετε ότι :
i) η είναι περιττή
είναι περιττή
ii) η έχει ένα σημείο καμπής το οποίο και να βρεθεί
έχει ένα σημείο καμπής το οποίο και να βρεθεί
iii) οι ευθείες και
και 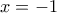 είναι ασύμπτωτες της
είναι ασύμπτωτες της 
γ) να βρείτε τα ώστε
ώστε 
δ) να δείξετε ότι το εμβαδόν που σχηματίζεται από τη γραφική παράσταση της , τον άξονα
, τον άξονα  και τις κατακόρυφες ευθείες
και τις κατακόρυφες ευθείες  ,
,  , όπου
, όπου  , είναι ίσο με :
, είναι ίσο με :

ΑΣΚΗΣΗ 22 (Τηλέγραφος-Παντούλας)
Δίνονται οι συναρτήσεις
 με
με  ,
,  .
.Αν
 , η
, η  παρουσιάζει ολικό ακρότατο μόνο στη θέση
παρουσιάζει ολικό ακρότατο μόνο στη θέση  το
το  και ισχύει
και ισχύει για κάθε
για κάθε  , τότε :
, τότε :α) να δείξετε ότι
 , για κάθε
, για κάθε 
β) να δείξετε ότι :
i) η
 είναι περιττή
είναι περιττήii) η
 έχει ένα σημείο καμπής το οποίο και να βρεθεί
έχει ένα σημείο καμπής το οποίο και να βρεθείiii) οι ευθείες
 και
και 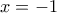 είναι ασύμπτωτες της
είναι ασύμπτωτες της 
γ) να βρείτε τα
 ώστε
ώστε 
δ) να δείξετε ότι το εμβαδόν που σχηματίζεται από τη γραφική παράσταση της
 , τον άξονα
, τον άξονα  και τις κατακόρυφες ευθείες
και τις κατακόρυφες ευθείες  ,
,  , όπου
, όπου  , είναι ίσο με :
, είναι ίσο με :
Λάμπρος Μπαλός
lamprosbalos81@gmail.com
lamprosbalos81@gmail.com
Re: Για τους μαθητές της Γ Λυκείου
Καλημέρα!Λάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 20 ΕΜΕ 2012
Εστω η παραγωγίσιμη συνάρτησημε συνεχή παράγωγο, που ικανοποιεί τις σχέσεις :
•, για κάθε
(1)
•(2)
•(3)
Α) Να αποδείξετε ότι,
Β) Να αποδείξετε ότιγια κάθε
Γ) Να μελετήσετε τη συνάρτησηως προς τη μονοτονία και την κυρτότητα
Δ) Αν,
, τότε :
... i) Να αποδείξετε ότι,
... ii) Να βρείτε το εμβαδόν του χωρίου που περικλείεται από τη, τον άξονα
και τις ευθείες με εξισώσεις
και
... iii) Να αποδείξετε ότι, για κάθε
A)

Η
 είναι συνεχής ως διαφορά συνεχών συναρτήσεων και
είναι συνεχής ως διαφορά συνεχών συναρτήσεων και 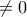 στο
στο  .
.Άρα θα διατηρεί πρόσημο και αφού
 τότε θα είναι
τότε θα είναι
Όμοια αποδεικνύεται ότι
 είναι
είναι 
Άρα

Η
 είναι συνεχής στο
είναι συνεχής στο  ως παραγωγίσιμη άρα θα είναι συνεχής και στο
ως παραγωγίσιμη άρα θα είναι συνεχής και στο  .
.Επομένως

Έχουμε τελικά

Β) Είναι

Γ) Έχουμε
 ,
,  γνησίως αύξουσα στο
γνησίως αύξουσα στο  .
. , η
, η  γν.αύξουσα
γν.αύξουσα  η
η  κυρτή στο
κυρτή στο  .
.Δ)


 Για κάθε
Για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) είναι
είναι  και συνεχής.
και συνεχής. Άρα

Θέτω
 τότε
τότε ![I=\int_{0}^{1}{\sqrt{x^{2}+1}dx}=\int_{0}^{\frac{\pi }{4}}{\frac{1}{cos^{3}u}du}=[\frac{\epsilon \varphi x}{cosx}]_{0}^{\frac{\pi }{4}}-\int_{0}^{\frac{\pi }{4}}{\frac{1}{cos^{3}x}dx}+\int_{0}^{\frac{\pi }{4}}{\frac{1}{cosx}dx}\Leftrightarrow 2I=2+\int_{0}^{\frac{\pi }{4}}{\frac{1}{cosx}dx} I=\int_{0}^{1}{\sqrt{x^{2}+1}dx}=\int_{0}^{\frac{\pi }{4}}{\frac{1}{cos^{3}u}du}=[\frac{\epsilon \varphi x}{cosx}]_{0}^{\frac{\pi }{4}}-\int_{0}^{\frac{\pi }{4}}{\frac{1}{cos^{3}x}dx}+\int_{0}^{\frac{\pi }{4}}{\frac{1}{cosx}dx}\Leftrightarrow 2I=2+\int_{0}^{\frac{\pi }{4}}{\frac{1}{cosx}dx}](/forum/ext/geomar/texintegr/latexrender/pictures/b0c4e2f7bd2c9eb9ae865bbd9cd1b06a.png)
Όμως
 Έθεσα
Έθεσα 
Βρίσκουμε το
 και συνεπώς και το
και συνεπώς και το  (θα τα έβρισκα αλλά έχω και διάβασμα).
(θα τα έβρισκα αλλά έχω και διάβασμα). Θεωρώ την συνάρτηση
Θεωρώ την συνάρτηση 

 η
η  γν αύξουσα
γν αύξουσα
Είναι
 και η
και η  συνεχής στο
συνεχής στο 
Άρα η
 γν.αύξουσα στο
γν.αύξουσα στο  .
.
Ελπίζω να μην έκανα κάποιο λάθος.
Re: Για τους μαθητές της Γ Λυκείου
α) ΗΛάμπρος Μπαλός έγραψε:Από Εκδόσεις Κανδύλας, μία άσκηση από τα Διαγωνίσματα εφ' όλης της ύλης που μου άρεσε
ΑΣΚΗΣΗ 22 (Τηλέγραφος-Παντούλας)
Δίνονται οι συναρτήσειςμε
,
.
Αν, η
παρουσιάζει ολικό ακρότατο μόνο στη θέση
το
και ισχύει
για κάθε
, τότε :
α) να δείξετε ότι, για κάθε
β) να δείξετε ότι :
i) ηείναι περιττή
ii) ηέχει ένα σημείο καμπής το οποίο και να βρεθεί
iii) οι ευθείεςκαι
είναι ασύμπτωτες της
γ) να βρείτε ταώστε
δ) να δείξετε ότι το εμβαδόν που σχηματίζεται από τη γραφική παράσταση της, τον άξονα
και τις κατακόρυφες ευθείες
,
, όπου
, είναι ίσο με :
 παρουσιάζει ολικό ακρότατο στη θέση
παρουσιάζει ολικό ακρότατο στη θέση  το
το  ,άρα υπάρχει μοναδική τιμή της
,άρα υπάρχει μοναδική τιμή της  για την οποία ισχύει
για την οποία ισχύει  και αυτή είναι το
και αυτή είναι το  .
.Συνεπώς είναι


Επομένως μπορούμε να διαιρέσουμε.


Για



Άρα

β)

 ισχύει και
ισχύει και 
Όπου
 το
το  και έχουμε:
και έχουμε: 
Άρα η
 είναι περιττή.
είναι περιττή. Από
Από  ερώτημα έχουμε
ερώτημα έχουμε  .Παραγωγίζουμε και παίρνουμε :
.Παραγωγίζουμε και παίρνουμε : 
 ,
, 
Η
 αλλάζει πρόσημο εκατέρωθεν του
αλλάζει πρόσημο εκατέρωθεν του  και είναι
και είναι  . Άρα η
. Άρα η  έχει ένα Σ.Κ. στο
έχει ένα Σ.Κ. στο  το
το 



Άρα οι ευθείες
 είναι κατακόρυφες ασύμπτωτες της
είναι κατακόρυφες ασύμπτωτες της  .
.γ)

Η
 είναι γνησίως αύξουσα, άρα και
είναι γνησίως αύξουσα, άρα και  .Τότε
.Τότε 
Για να ισχύει αυτό πρέπει:
 και
και  , δηλαδή
, δηλαδή 
δ)Η
 είναι περιττή, τότε λόγω συμμετρίας το ζητούμενο εμβαδόν θα είναι ίσο με:
είναι περιττή, τότε λόγω συμμετρίας το ζητούμενο εμβαδόν θα είναι ίσο με: 
Re: Για τους μαθητές της Γ Λυκείου
α) Ικανοποιούνται οι προϋποθέσει L'Hospital:Christos.N έγραψε:Άσκηση 18
Δίνεται η παραγωγίσιμη συνάρτησημε
για την οποία ισχύει
.
1) Να δείξετε ότι
2) Να βρεθεί το σύνολο τιμών της.
3) Αν, να αποδείξετε ότι
.
4) ΝΑ δείξετε ότι η εξίσωσηέχει μοναδική ρίζα στο
.
Μαθηματικά Γ' τάξης Γενικού Λυκείου , Εκδόσεις Κανδύλας

Άρα

Επομένως

Για



Συνεπώς

β)

και αφού η
 συνεχής στο
συνεχής στο  τότε η
τότε η  γν.φθίνουσα στο πεδίο ορισμού της.
γν.φθίνουσα στο πεδίο ορισμού της.Άρα
 γιατί:
γιατί: αφού
αφού 

γ)
 και έπεται το ζητούμενο.
και έπεται το ζητούμενο.δ)Έστω η συνάρτηση

Προφανής ρίζα το
 .Χτίζοντας την από
.Χτίζοντας την από  καταλήγουμε μετά από αρκετές σειρές σε
καταλήγουμε μετά από αρκετές σειρές σε  .
.Άρα η
 και το
και το  ρίζα της άρα και μοναδική.
ρίζα της άρα και μοναδική.Δηλαδή η εξίσωση
 έχει μοναδική ρίζα στο
έχει μοναδική ρίζα στο  και μάλιστα την
και μάλιστα την  .
.Σίγουρα πρέπει να υπάρχει και άλλος τρόπος για το (δ), τον οποίο δεν τον βλέπω αυτή τη στιγμή.
Re: Για τους μαθητές της Γ Λυκείου
ΑΣΚΗΣΗ 23
Έστω η συνάρτηση , για την οποία ισχύει
, για την οποία ισχύει  , για κάθε
, για κάθε  .
.
A. Να υπολογίσετε το .
.
B. Να δείξετε ότι η είναι συνεχής στο
είναι συνεχής στο  .
.
Γ. Να δείξετε ότι η είναι περιττή στο
είναι περιττή στο  .
.
Δ. Να μελετήσετε τη συνάρτηση ως προς τη μονοτονία και το σύνολο τιμών της.
ως προς τη μονοτονία και το σύνολο τιμών της.
Φιλικά,
Μάριος
Έστω η συνάρτηση
 , για την οποία ισχύει
, για την οποία ισχύει  , για κάθε
, για κάθε  .
.A. Να υπολογίσετε το
 .
.B. Να δείξετε ότι η
 είναι συνεχής στο
είναι συνεχής στο  .
.Γ. Να δείξετε ότι η
 είναι περιττή στο
είναι περιττή στο  .
.Δ. Να μελετήσετε τη συνάρτηση
 ως προς τη μονοτονία και το σύνολο τιμών της.
ως προς τη μονοτονία και το σύνολο τιμών της.Φιλικά,
Μάριος
Είναι αυταπάτη ότι η νεότητα είναι ευτυχισμένη, μια αυταπάτη αυτών που την έχουν χάσει. W. Somerset Maugham
Re: Για τους μαθητές της Γ Λυκείου
M.S.Vovos έγραψε:ΑΣΚΗΣΗ 23
Έστω η συνάρτηση, για την οποία ισχύει
, για κάθε
.
A. Να υπολογίσετε το.
B. Να δείξετε ότι ηείναι συνεχής στο
.
Γ. Να δείξετε ότι ηείναι περιττή στο
.
Δ. Να μελετήσετε τη συνάρτησηως προς τη μονοτονία και το σύνολο τιμών της.
Φιλικά,
Μάριος
Αυτή η άσκηση είναι εκτός πνεύματος εξετάσεων (ο σκοπός του παρόντος θρέντ).
Εν τούτοις, από μαθηματικής σκοπιάς φαίνεται όμορφη άρα ας δώσουμε μια λύση.
Α)
Για
 στην δοθείσα παίρνουμε
στην δοθείσα παίρνουμε 
Συνεπώς,
 .
.Επίσης,



Με χρήση του κριτηρίου παρεμβολής εύκολα δείχνουμε ότι

Και εφόσον
 ,
,
Ισχύει ότι

Επομένως,
![\displaystyle{\lim_{x\rightarrow +\infty}\frac{f(x)}{x}=\lim_{x\rightarrow +\infty}\sqrt[3]{1-\frac{f(x)}{x^3}}=\sqrt[3]{\lim_{x\rightarrow +\infty}\left( 1-\frac{f(x)}{x^3}\right)}=1} \displaystyle{\lim_{x\rightarrow +\infty}\frac{f(x)}{x}=\lim_{x\rightarrow +\infty}\sqrt[3]{1-\frac{f(x)}{x^3}}=\sqrt[3]{\lim_{x\rightarrow +\infty}\left( 1-\frac{f(x)}{x^3}\right)}=1}](/forum/ext/geomar/texintegr/latexrender/pictures/9efdaf458827dd2cb10d030d062099a3.png)
Β)
Έστω τυχαίο

Τότε,

Την αφαιρώ από από την αρχική και έχω:

Παίρνοντας όρια, έχω:
![\displaystyle{\Rightarrow \lim_{x\rightarrow x_o}\left[ \left(f(x)-f(x_o) \right)\left(\left(f(x)+\frac{f(x_o)}{2} \right)^2 +3\frac{f^2(x_o)}{4} \right)\right]=\lim_{x\rightarrow x_o}\left[ (x-x_o)(x^2 +xx_o+x_o^2)\right]=0} \displaystyle{\Rightarrow \lim_{x\rightarrow x_o}\left[ \left(f(x)-f(x_o) \right)\left(\left(f(x)+\frac{f(x_o)}{2} \right)^2 +3\frac{f^2(x_o)}{4} \right)\right]=\lim_{x\rightarrow x_o}\left[ (x-x_o)(x^2 +xx_o+x_o^2)\right]=0}](/forum/ext/geomar/texintegr/latexrender/pictures/fd8eaf5631730c4454afc9bea9e32fc4.png)

Γ)
Θεωρώ συνάρτηση

Εύκολα αποδεικνύουμε ότι η
 είναι
είναι 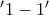 (Θα το δείξουμε και παρακάτω)
(Θα το δείξουμε και παρακάτω) και παρατηρούμε ότι,
και παρατηρούμε ότι, εφόσον η
εφόσον η  είναι
είναι 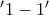
Άλλος ένας τρόπος είναι να θέσουμε όπου
 στην δοθείσα.Αφαιρώ την σχέση από την δοθείσα και καταλήγω σχετικά εύκολα στο ζητούμενο.
στην δοθείσα.Αφαιρώ την σχέση από την δοθείσα και καταλήγω σχετικά εύκολα στο ζητούμενο.Δ)
Έστω

 διότι
διότι  γνησίως αύξουσα.
γνησίως αύξουσα.Άρα
 γνησίως αύξουσα.
γνησίως αύξουσα.Έχουμε δείξει παραπάνω ότι

Εφόσον η
 είναι γνησίως αύξουσα και
είναι γνησίως αύξουσα και  , δεν μπορεί να ισχύει
, δεν μπορεί να ισχύει 
Άρα θα ισχύει είτε
 είτε
είτε  .
.Έστω ότι
 .
.Τότε, από την δοθείσα:


ΑΤΟΠΟ.
Άρα
 .
.Οπότε εφόσον η
 είναι συνεχής και γνησίως αύξουσα στο πεδίο ορισμού της, θα ισχύει ότι,
είναι συνεχής και γνησίως αύξουσα στο πεδίο ορισμού της, θα ισχύει ότι,
Re: Για τους μαθητές της Γ Λυκείου
Ικανοποιούνται οι προϋποθέσει L'Hospital:
Nίκο αυτο που έκανες δεν γίνεται .πρόσεξε λίγο.Στην χρήση του θεωρ'ηματος θέλει προσοχή ...
φιλικά

Nίκο αυτο που έκανες δεν γίνεται .πρόσεξε λίγο.Στην χρήση του θεωρ'ηματος θέλει προσοχή ...
φιλικά
Dennys =Ξεκλείδωμα κάθε άσκησης
- Λάμπρος Μπαλός
- Δημοσιεύσεις: 984
- Εγγραφή: Τρί Αύγ 13, 2013 12:21 pm
- Τοποθεσία: Τρίκαλα
Re: Για τους μαθητές της Γ Λυκείου
ΑΣΚΗΣΗ 24 (προσωπική πηγή : Μαθηματικά Γ Λυκείου Θετικής και Τεχνολογικής Κατ/σης, Δημήτριος Κατσαρός, Ελληνοεκδοτική)
Θεωρούμε μία συνάρτηση που έχει πεδίο ορισμού το
που έχει πεδίο ορισμού το  όπου και είναι δύο φορές παραγωγίσιμη.
όπου και είναι δύο φορές παραγωγίσιμη.
i) Αν υποθέσουμε ότι , να βρείτε τις τιμές
, να βρείτε τις τιμές  και
και  .
.
ii) Αν υποθέσουμε ότι για τους πραγματικούς , με
, με  , οι
, οι  είναι ομόσημοι και ισχύει
είναι ομόσημοι και ισχύει  , να αποδείξετε ότι υπάρχει ένα τουλάχιστον
, να αποδείξετε ότι υπάρχει ένα τουλάχιστον  τέτοιο, ώστε
τέτοιο, ώστε 
iii) Αν υποθέσουμε ότι για την ισχύει
ισχύει  και
και  , να αποδείξετε ότι υπάρχει
, να αποδείξετε ότι υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  για κάθε
για κάθε  .
.
Θεωρούμε μία συνάρτηση
 που έχει πεδίο ορισμού το
που έχει πεδίο ορισμού το  όπου και είναι δύο φορές παραγωγίσιμη.
όπου και είναι δύο φορές παραγωγίσιμη.i) Αν υποθέσουμε ότι
 , να βρείτε τις τιμές
, να βρείτε τις τιμές  και
και  .
.ii) Αν υποθέσουμε ότι για τους πραγματικούς
 , με
, με  , οι
, οι  είναι ομόσημοι και ισχύει
είναι ομόσημοι και ισχύει  , να αποδείξετε ότι υπάρχει ένα τουλάχιστον
, να αποδείξετε ότι υπάρχει ένα τουλάχιστον  τέτοιο, ώστε
τέτοιο, ώστε 
iii) Αν υποθέσουμε ότι για την
 ισχύει
ισχύει  και
και  , να αποδείξετε ότι υπάρχει
, να αποδείξετε ότι υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  για κάθε
για κάθε  .
.Λάμπρος Μπαλός
lamprosbalos81@gmail.com
lamprosbalos81@gmail.com
Re: Για τους μαθητές της Γ Λυκείου
Άσκηση 25 ..... Για τη δις παραγωγίσιμη συνάρτηση  ,
,
ισχύουν : .
.
α) Δείξτε ότι .
.
β) Δείξτε ότι η έχει μοναδική ρίζα .
έχει μοναδική ρίζα .
γ) Βρείτε τη μέγιστη τιμή που μπορεί να πάρει η κλίση μιας εφαπτομένης της .
.
δ) Αν η παρουσιάζει μέγιστο για
παρουσιάζει μέγιστο για  και σημείο καμπής για
και σημείο καμπής για  , βρείτε το
, βρείτε το
εμβαδόν του χωρίου που περικλείουν η , ο άξονας
, ο άξονας  και οι ευθείες
και οι ευθείες  .
.
 ,
,ισχύουν :
 .
.α) Δείξτε ότι
 .
.β) Δείξτε ότι η
 έχει μοναδική ρίζα .
έχει μοναδική ρίζα .γ) Βρείτε τη μέγιστη τιμή που μπορεί να πάρει η κλίση μιας εφαπτομένης της
 .
.δ) Αν η
 παρουσιάζει μέγιστο για
παρουσιάζει μέγιστο για  και σημείο καμπής για
και σημείο καμπής για  , βρείτε το
, βρείτε τοεμβαδόν του χωρίου που περικλείουν η
 , ο άξονας
, ο άξονας  και οι ευθείες
και οι ευθείες  .
.Re: Για τους μαθητές της Γ Λυκείου
Καλησπέρα.Λάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 24 (προσωπική πηγή : Μαθηματικά Γ Λυκείου Θετικής και Τεχνολογικής Κατ/σης, Δημήτριος Κατσαρός, Ελληνοεκδοτική)
Θεωρούμε μία συνάρτησηπου έχει πεδίο ορισμού το
όπου και είναι δύο φορές παραγωγίσιμη.
i) Αν υποθέσουμε ότι, να βρείτε τις τιμές
και
.
ii) Αν υποθέσουμε ότι για τους πραγματικούς, με
, οι
είναι ομόσημοι και ισχύει
, να αποδείξετε ότι υπάρχει ένα τουλάχιστον
τέτοιο, ώστε
iii) Αν υποθέσουμε ότι για τηνισχύει
και
, να αποδείξετε ότι υπάρχει
τέτοιο, ώστε
για κάθε
.
 δύο φορές παραγωγίσιμη άρα η
δύο φορές παραγωγίσιμη άρα η  συνεχείς.
συνεχείς.i)
Θεωρώ συνάρτηση
 .
. κοντά στο
κοντά στο  ,
,
Άρα


Θεωρώ συνάρτηση

Κοντά στο
 ,
, 
Οπότε,

ii)
 ομόσημοι άρα θα ισχύει
ομόσημοι άρα θα ισχύει 
Η
 πληροί τις προυποθέσεις του
πληροί τις προυποθέσεις του  στο
στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) και στο
και στο ![[b,c] [b,c]](/forum/ext/geomar/texintegr/latexrender/pictures/238bb374974bd3b5bf3b51c245fb1bdc.png) .
.Άρα

και

Τώρα, η
 πληροί τις προυποθέσεις του θεωρήματος
πληροί τις προυποθέσεις του θεωρήματος  στο
στο ![[\xi_1,\xi_2] [\xi_1,\xi_2]](/forum/ext/geomar/texintegr/latexrender/pictures/aa22922e8d953a40abce3c8f1e68e9b4.png)
με

Οπότε
![\exists \xi \in [\xi_1,\xi_2]: \boxed{f'(\xi)=0} \exists \xi \in [\xi_1,\xi_2]: \boxed{f'(\xi)=0}](/forum/ext/geomar/texintegr/latexrender/pictures/45c429749f0cb544af3914999230f7b5.png)
iii)


Για



Re: Για τους μαθητές της Γ Λυκείου
KARKAR έγραψε:Άσκηση 25 ..... Για τη δις παραγωγίσιμη συνάρτηση,
ισχύουν :.
α) Δείξτε ότι.
β) Δείξτε ότι ηέχει μοναδική ρίζα .
γ) Βρείτε τη μέγιστη τιμή που μπορεί να πάρει η κλίση μιας εφαπτομένης της.
δ) Αν ηπαρουσιάζει μέγιστο για
και σημείο καμπής για
, βρείτε το
εμβαδόν του χωρίου που περικλείουν η, ο άξονας
και οι ευθείες
.
Μια αντιμετώπιση,
α)


Για


Για

Κάνουμε και μια επαλήθευση και είμαστε jet.
β)

Οπότε η
 γνησίως αύξουσα στο
γνησίως αύξουσα στο ![\left(-\infty,0 \right] \left(-\infty,0 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/ebab3376a9700fcd0bd6d09ecd4cd88e.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο  .
.![f( \left[0,+\infty \right))=\left(-\infty,2 \right] f( \left[0,+\infty \right))=\left(-\infty,2 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/c5a790750666f87d2ae98f0cd6d5eb1e.png) και
και ![f( \left(-\infty,0 \right])=\left(1,2 \right] f( \left(-\infty,0 \right])=\left(1,2 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/45abe5b1d26b9f8e1413d1b3bb26ae8d.png)
![0 \notin f( \left(-\infty,0 \right]) 0 \notin f( \left(-\infty,0 \right])](/forum/ext/geomar/texintegr/latexrender/pictures/762b6c1a1a0aee5b176cd997fee0bf3f.png)
ενώ
 και
και  γνησίως μονότονη σε αυτό άρα θα
γνησίως μονότονη σε αυτό άρα θα 
Και μάλιστα εφαρμόζοντας το
 δείχνουμε ότι
δείχνουμε ότι  .
.γ)
Θεωρώ συνάρτηση

Η
 γνησίως αύξουσα στο
γνησίως αύξουσα στο ![(-\infty,-1] (-\infty,-1]](/forum/ext/geomar/texintegr/latexrender/pictures/7868576f01d6787f4e7c63c6d1bde23c.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο 
Άρα παρουσιάζει μέγιστο στο
 το
το  που είναι η ζητούμενη τιμή.
που είναι η ζητούμενη τιμή.δ)
![\displaystyle{\forall x\in (-\infty,0]: f(x)\in (1,2] \Rightarrow f(x)>0} \displaystyle{\forall x\in (-\infty,0]: f(x)\in (1,2] \Rightarrow f(x)>0}](/forum/ext/geomar/texintegr/latexrender/pictures/d4b9fca5955ace5e664f0d4c958b2189.png)
![\displaystyle{\Rightarrow E(\Omega )=\int_{-1}^{0}(-xe^x +e^x +1)dx=\left[-xe^x \right]_{-1}^0 +2\left[e^x \right]_{-1}^0 +\left[x \right]_{-1}^0=3-\frac{3}{e}} \displaystyle{\Rightarrow E(\Omega )=\int_{-1}^{0}(-xe^x +e^x +1)dx=\left[-xe^x \right]_{-1}^0 +2\left[e^x \right]_{-1}^0 +\left[x \right]_{-1}^0=3-\frac{3}{e}}](/forum/ext/geomar/texintegr/latexrender/pictures/1f23babbd2981ff55757b9a38658746e.png)
Re: Για τους μαθητές της Γ Λυκείου
ΑΣΚΗΣΗ 26
Θεωρούμε την και τρεις φορές παραγωγίσιμη συνάρτηση
και τρεις φορές παραγωγίσιμη συνάρτηση  , για την οποία ισχύουν:
, για την οποία ισχύουν:
![\displaystyle \bullet f\left ( 6f(x)-x^{2}f''(x) \right )=\left [ 6f'(x)-2xf''(x)-x^{2}f^{(3)}(x) \right ]\cdot f'\left ( 6f(x)-x^{2}f''(x) \right ) \displaystyle \bullet f\left ( 6f(x)-x^{2}f''(x) \right )=\left [ 6f'(x)-2xf''(x)-x^{2}f^{(3)}(x) \right ]\cdot f'\left ( 6f(x)-x^{2}f''(x) \right )](/forum/ext/geomar/texintegr/latexrender/pictures/632c3aeef282027e6f80d0ddafba435e.png) , για κάθε
, για κάθε  .
.

A. Να δείξετε ότι ,
,  .
.
B. Να βρείτε το εμβαδόν του χωρίου, που περικλείεται από τη και την ευθεία
και την ευθεία  , με
, με  .
.
Γ. Να βρείτε το πλήθος των πραγματικών ριζών της εξίσωσης .
.
Δ. Έστω τα σημεία ,
,  και
και  . Να δείξετε ότι υπάρχουν ακριβώς δύο
. Να δείξετε ότι υπάρχουν ακριβώς δύο  ώστε τα παραπάνω σημεία να είναι συνευθειακά.
ώστε τα παραπάνω σημεία να είναι συνευθειακά.
Ε. Να βρείτε τα ώστε
ώστε  .
.
Φιλικά,
Μάριος
Θεωρούμε την
 και τρεις φορές παραγωγίσιμη συνάρτηση
και τρεις φορές παραγωγίσιμη συνάρτηση  , για την οποία ισχύουν:
, για την οποία ισχύουν:![\displaystyle \bullet f\left ( 6f(x)-x^{2}f''(x) \right )=\left [ 6f'(x)-2xf''(x)-x^{2}f^{(3)}(x) \right ]\cdot f'\left ( 6f(x)-x^{2}f''(x) \right ) \displaystyle \bullet f\left ( 6f(x)-x^{2}f''(x) \right )=\left [ 6f'(x)-2xf''(x)-x^{2}f^{(3)}(x) \right ]\cdot f'\left ( 6f(x)-x^{2}f''(x) \right )](/forum/ext/geomar/texintegr/latexrender/pictures/632c3aeef282027e6f80d0ddafba435e.png) , για κάθε
, για κάθε  .
.

A. Να δείξετε ότι
 ,
,  .
.B. Να βρείτε το εμβαδόν του χωρίου, που περικλείεται από τη
 και την ευθεία
και την ευθεία  , με
, με  .
.Γ. Να βρείτε το πλήθος των πραγματικών ριζών της εξίσωσης
 .
.Δ. Έστω τα σημεία
 ,
,  και
και  . Να δείξετε ότι υπάρχουν ακριβώς δύο
. Να δείξετε ότι υπάρχουν ακριβώς δύο  ώστε τα παραπάνω σημεία να είναι συνευθειακά.
ώστε τα παραπάνω σημεία να είναι συνευθειακά.Ε. Να βρείτε τα
 ώστε
ώστε  .
.Φιλικά,
Μάριος
Είναι αυταπάτη ότι η νεότητα είναι ευτυχισμένη, μια αυταπάτη αυτών που την έχουν χάσει. W. Somerset Maugham
- Λάμπρος Μπαλός
- Δημοσιεύσεις: 984
- Εγγραφή: Τρί Αύγ 13, 2013 12:21 pm
- Τοποθεσία: Τρίκαλα
Re: Για τους μαθητές της Γ Λυκείου
Αφορμής δοθείσης από μια παρατήρηση του Χρήστου Ντάβα.Λάμπρος Μπαλός έγραψε:ΑΣΚΗΣΗ 24 (προσωπική πηγή : Μαθηματικά Γ Λυκείου Θετικής και Τεχνολογικής Κατ/σης, Δημήτριος Κατσαρός, Ελληνοεκδοτική)
Θεωρούμε μία συνάρτησηπου έχει πεδίο ορισμού το
όπου και είναι δύο φορές παραγωγίσιμη.
i) Αν υποθέσουμε ότι, να βρείτε τις τιμές
και
.
ii) Αν υποθέσουμε ότι για τους πραγματικούς, με
, οι
είναι ομόσημοι και ισχύει
, να αποδείξετε ότι υπάρχει ένα τουλάχιστον
τέτοιο, ώστε
iii) Αν υποθέσουμε ότι για τηνισχύει
και
, να αποδείξετε ότι υπάρχει
τέτοιο, ώστε
για κάθε
.
Ας λύσουμε τα δύο πρώτα ερωτήματα γνωρίζοντας ότι η
 είναι μία φορά παραγωγίσιμη και όχι δύο. Πιστεύω για τους μαθητές έχουν αξία!
είναι μία φορά παραγωγίσιμη και όχι δύο. Πιστεύω για τους μαθητές έχουν αξία!Χρήστο σε ευχαριστώ!
Λάμπρος Μπαλός
lamprosbalos81@gmail.com
lamprosbalos81@gmail.com
- Tolaso J Kos
- Δημοσιεύσεις: 5225
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Για τους μαθητές της Γ Λυκείου
Επαναφορά. Αν και την ιδέα μάλλον την έχω ξανά βάλει. Δε πειράζει.Tolaso J Kos έγραψε:Άσκηση 16 (από περιοδικό)
Έστωη οποία ορίζεται ως εξής:
. Να δείξετε ότι είναι συνεχής στο
και να υπολογίσετε το εμβαδόν του χωρίου
που περικλείεται της
, του άξονα
και των ευθειών
.
Είχε και άλλα ερωτήματα (όπως κυρτότητα, σύνολο τιμών κτλ) αλλά δε τα προσθέτω αφού είναι αρκετά γνωστά ως "μεθοδολογίες" και αρκετά χρονοβόρα στο γράψιμο.
Η φαντασία είναι σημαντικότερη από τη γνώση !


Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες






