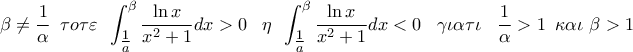Σελίδα 1 από 1
Γενικό θέμα , αλλά με δυσκολίες !
Δημοσιεύτηκε: Κυρ Μάιος 01, 2011 1:34 pm
από Μπάμπης Στεργίου
Καμιά φορά χωρίς τα υποερωτήματα,τα πράγματα γίνονται δύσκολα !!!
Μια παραγωγίσιμη συνάρτηση

με
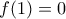
έχει την ιδιότητα :

.
α) Να αποδείξετε ότι
 β)
β) Να υπολογίσετε το ολοκλήρωμα
 γ)
γ) Αν
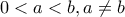
και
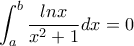
, να αποδειχθεί ότι

και

Μπάμπης
Re: Γενικό θέμα , αλλά με δυσκολίες !
Δημοσιεύτηκε: Κυρ Μάιος 01, 2011 2:47 pm
από hsiodos
Μπάμπη καλό μεσημέρι , μια αντιμετώπιση
α) Για κάθε x > 0 έχουμε:
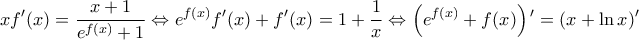
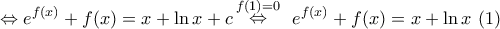
Θεωρούμε την συνάρτηση
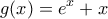
που είναι ορισμένη στο R και 1-1 (εύκολο)
Για κάθε x > 0 έχουμε:
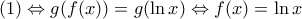
β) Θέτουμε

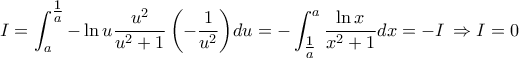
γ)
![\displaystyle{
{\rm A}\nu \,\,0 < \alpha < \beta \le 1\,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\,\,\, < 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \le 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]\,} \displaystyle{
{\rm A}\nu \,\,0 < \alpha < \beta \le 1\,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\,\,\, < 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \le 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]\,}](/forum/ext/geomar/texintegr/latexrender/pictures/85550d793a9658ef93655e55c381d6cd.png)
(το ίσον ισχύει μόνο αν x = β =1)
![\displaystyle{
{\rm A}\nu \,\,\,1 \le \alpha < \beta \,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\, > 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \ge 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]} \displaystyle{
{\rm A}\nu \,\,\,1 \le \alpha < \beta \,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\, > 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \ge 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/bce08551c1aa34b81edc54c7be576c8b.png)
(το ίσον ισχύει μόνο αν x = α =1)
Επομένως 0 < α < 1 < β
Τώρα

αφού αν
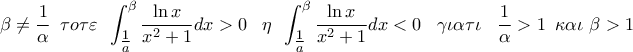
Γιώργος
Re: Γενικό θέμα , αλλά με δυσκολίες !
Δημοσιεύτηκε: Κυρ Μάιος 01, 2011 5:36 pm
από chris_gatos
Υπήρχε και --->
εδώ με μία πολύ ωραία
επεξήγηση του Μιχάλη.
Re: Γενικό θέμα , αλλά με δυσκολίες !
Δημοσιεύτηκε: Κυρ Μάιος 01, 2011 10:09 pm
από Μπάμπης Στεργίου
chris_gatos έγραψε:Υπήρχε και --->
εδώ με μία πολύ ωραία
επεξήγηση του Μιχάλη.
Χρήστο, ευχαριστώ !
Είχα διαβάσει και γω όλη τη σχετική αλληλογραφία και δε μπορούσα να βρω το σύνδεσμο.
Αλλά και παλιότερα το είχαμε ξανακουβεντιάσει, αλλά πάλι δεν το βρίσκω, αν και πριν από έναπερίπου μήνα έπεσα πάνω του κατά τύχη.
Αν τύχει καμιά φορά και το βρεις, στείλε τον.
Μπάμπης
 με
με 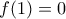 έχει την ιδιότητα :
έχει την ιδιότητα : .
.

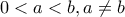 και
και 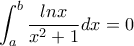 , να αποδειχθεί ότι
, να αποδειχθεί ότι  και
και 
 με
με 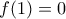 έχει την ιδιότητα :
έχει την ιδιότητα : .
.

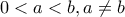 και
και 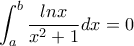 , να αποδειχθεί ότι
, να αποδειχθεί ότι  και
και 
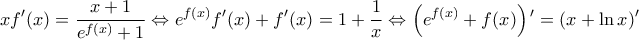
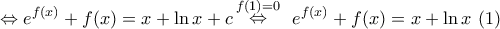
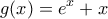 που είναι ορισμένη στο R και 1-1 (εύκολο)
που είναι ορισμένη στο R και 1-1 (εύκολο)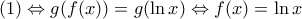

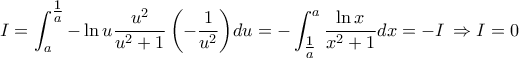
![\displaystyle{
{\rm A}\nu \,\,0 < \alpha < \beta \le 1\,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\,\,\, < 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \le 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]\,} \displaystyle{
{\rm A}\nu \,\,0 < \alpha < \beta \le 1\,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\,\,\, < 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \le 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]\,}](/forum/ext/geomar/texintegr/latexrender/pictures/85550d793a9658ef93655e55c381d6cd.png) (το ίσον ισχύει μόνο αν x = β =1)
(το ίσον ισχύει μόνο αν x = β =1)![\displaystyle{
{\rm A}\nu \,\,\,1 \le \alpha < \beta \,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\, > 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \ge 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]} \displaystyle{
{\rm A}\nu \,\,\,1 \le \alpha < \beta \,\,\,\tau o\tau \varepsilon \,\,\,\int_\alpha ^\beta {\frac{{\ln x}}{{x^2 + 1}}dx\, > 0\,\,\,\alpha \phi o\upsilon \,\,} \frac{{\ln x}}{{x^2 + 1}} \ge 0\,\,\,\gamma \iota \alpha \,\,\,\kappa \alpha \theta \varepsilon \,\,x \in \left[ {a,\beta } \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/bce08551c1aa34b81edc54c7be576c8b.png) (το ίσον ισχύει μόνο αν x = α =1)
(το ίσον ισχύει μόνο αν x = α =1)