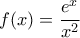 .
.- Να μελετηθεί η
 ως προς τη μονοτονία και τα ακρότατα.
ως προς τη μονοτονία και τα ακρότατα. - Αν
 το εμβαδόν του χωρίου που περικλείεται της
το εμβαδόν του χωρίου που περικλείεται της 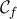 , του άξονα
, του άξονα  και των ευθειών
και των ευθειών  ,
,  τότε να δειχθεί ότι
τότε να δειχθεί ότι 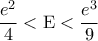
Συντονιστής: R BORIS
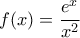 .
. ως προς τη μονοτονία και τα ακρότατα.
ως προς τη μονοτονία και τα ακρότατα. το εμβαδόν του χωρίου που περικλείεται της
το εμβαδόν του χωρίου που περικλείεται της  , του άξονα
, του άξονα  και των ευθειών
και των ευθειών  ,
,  τότε να δειχθεί ότι
τότε να δειχθεί ότι 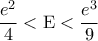

i.Tolaso J Kos έγραψε: ↑Παρ Οκτ 01, 2021 10:48 amΔίδεται η συνάρτηση.
- Να μελετηθεί η
ως προς τη μονοτονία και τα ακρότατα.
- Αν
το εμβαδόν του χωρίου που περικλείεται της
, του άξονα
και των ευθειών
,
τότε να δειχθεί ότι

 είναι γνησίως αύξουσα σε καθένα από τα διαστήματα
είναι γνησίως αύξουσα σε καθένα από τα διαστήματα  και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![(0,2]. (0,2].](/forum/ext/geomar/texintegr/latexrender/pictures/cb34ddfc5d1c9ae48e6f576576ac5f14.png)
 παρουσιάζει τοπικό ελάχιστο ίσο με
παρουσιάζει τοπικό ελάχιστο ίσο με 
 και το ζητούμενο έπεται.
και το ζητούμενο έπεται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες