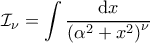 όπου
όπου  . Να δειχθεί ότι:
. Να δειχθεί ότι:
Συντονιστής: R BORIS
Μη αναγνωσμένη δημοσίευση από Tolaso J Kos » Κυρ Ιούλ 04, 2021 12:17 pm
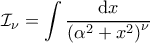 όπου
όπου  . Να δειχθεί ότι:
. Να δειχθεί ότι:

Μη αναγνωσμένη δημοσίευση από Mihalis_Lambrou » Κυρ Ιούλ 04, 2021 2:55 pm
Με κατά παράγοντες έχουμε


 (γραμμική και απλή).
(γραμμική και απλή).Επιστροφή σε “ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off