Η ιδέα είναι τα ολοκληρώματα να μην είναι ρουτίνας αλλά να μην φτάνουμε στο άλλο άκρο των
ολοκληρωμάτων που εμφανίζονται σε διαγωνισμούς για φοιτητές.
Πρέπει να είναι προσιτά με γνώσεις Λυκείου, τουλάχιστον όπως ήταν η ύλη λίγα χρόνια νωρίτερα πριν
καταργηθούν όσα καταργήθηκαν (τα οποία έπαψα να παρακολουθώ στις λεπτομέρειες γιατί δεν βγάζω άκρη. Και δεν τα κατανοώ.)
Απαγορεύονται ασκήσεις που απαιτούν συναρτήσεις
 , δυναμοσειρές και λοιπά.
, δυναμοσειρές και λοιπά.
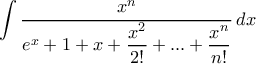
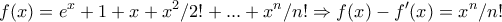
 το ζητούμενο ολοκλήρωμα
το ζητούμενο ολοκλήρωμα
 όπου
όπου  .
. τότε
τότε 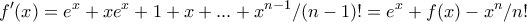


![\displaystyle{ I_n= \int_{0}^{x}{e^{-t}t^ndt} = \left [ -e^{-t}t^n \right ]_0^x+n\int_{0}^{x}{e^{-t}t^{n-1}dt = -e^{-x}x^n+ nI_{n-1}} \displaystyle{ I_n= \int_{0}^{x}{e^{-t}t^ndt} = \left [ -e^{-t}t^n \right ]_0^x+n\int_{0}^{x}{e^{-t}t^{n-1}dt = -e^{-x}x^n+ nI_{n-1}}](/forum/ext/geomar/texintegr/latexrender/pictures/c8a108925af473130f93d5d3d1b30e8b.png)
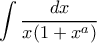 , όπου
, όπου  και
και 





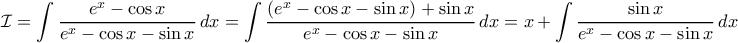
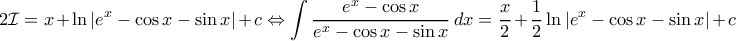


 , δοκιμάζουμε αν ο αριθμητής γράφεται στην μορφή
, δοκιμάζουμε αν ο αριθμητής γράφεται στην μορφή  για σταθερές
για σταθερές  .
. 
 .
. , οπότε
, οπότε  . Με άλλα λόγια
. Με άλλα λόγια 
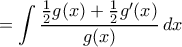
 , όπου
, όπου  φυσικός.
φυσικός. το ολοκλήρωμα. Τότε,
το ολοκλήρωμα. Τότε,

 και δε ξέρω το γιατί;
και δε ξέρω το γιατί;
 .
.
![\displaystyle{\begin{aligned}
\int_{\pi/3}^{2\pi/3} \frac{\mathrm{d}x}{\sin x} &= \int_{\pi/3}^{2\pi/3} \frac{\sin x}{\sin^2 x}\, \mathrm{d}x \\
&=\int_{\pi/3}^{2\pi/3} \frac{\sin x}{1-\cos^2 x}\, \mathrm{d}x \\
&\!\!\!\!\!\!\overset{u=\cos x}{=\!=\!=\!=\!=\!} \int_{-1/2}^{1/2} \frac{\mathrm{d}u}{1-u^2} \\
&=\frac{1}{2}\int_{-1/2}^{1/2}\left ( \frac{1}{u+1}-\frac{1}{u-1} \right ) \, \mathrm{d}u \\
&= \frac{1}{2} \left [ \ln \left | u+1 \right | - \ln \left | u-1 \right | \right ]_{-1/2}^{1/2}\\
&=\frac{\ln 9}{2}\\
&= \ln \sqrt{9}\\
&= \ln 3
\end{aligned}} \displaystyle{\begin{aligned}
\int_{\pi/3}^{2\pi/3} \frac{\mathrm{d}x}{\sin x} &= \int_{\pi/3}^{2\pi/3} \frac{\sin x}{\sin^2 x}\, \mathrm{d}x \\
&=\int_{\pi/3}^{2\pi/3} \frac{\sin x}{1-\cos^2 x}\, \mathrm{d}x \\
&\!\!\!\!\!\!\overset{u=\cos x}{=\!=\!=\!=\!=\!} \int_{-1/2}^{1/2} \frac{\mathrm{d}u}{1-u^2} \\
&=\frac{1}{2}\int_{-1/2}^{1/2}\left ( \frac{1}{u+1}-\frac{1}{u-1} \right ) \, \mathrm{d}u \\
&= \frac{1}{2} \left [ \ln \left | u+1 \right | - \ln \left | u-1 \right | \right ]_{-1/2}^{1/2}\\
&=\frac{\ln 9}{2}\\
&= \ln \sqrt{9}\\
&= \ln 3
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/bae958a0ed0661c708bdac51c8f3a3ee.png)
 .
.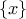 είναι το κλασματικό μέρος του
είναι το κλασματικό μέρος του  . Επιτρέπεται να χρησιμοποιήσετε αυτά που βρήκε ο Τόλης στο αμέσως προηγούμενο ποστ.
. Επιτρέπεται να χρησιμοποιήσετε αυτά που βρήκε ο Τόλης στο αμέσως προηγούμενο ποστ.