.Tolaso J Kos έγραψε: ↑Δευ Ιούλ 13, 2020 10:39 pmΈκανα compile κάποια από τα πρόβλημα ( μόνο εκφωνήσεις ) που βρίσκονται στο thread εδώ.
Ευχαριστούμε.
Επίσης για την πάλαι ποτέ
έχουμε την λύση
Τελικά το ολοκήρωμα αυτό μπορεί να βγει με πολλούς τρόπους (τουλάχιστον τρεις). Ένας είναι: Με την αλλαγή μεταβλητήςTolaso J Kos έγραψε: ↑Τετ Δεκ 18, 2019 2:34 pm
Κάνουμε την αλλαγή μεταβλητήςοπότε έχουμε, αν
το ολοκλήρωμα τότε:

 , οπότε
, οπότε  έχουμε
έχουμε  , το οποίο σύμφωνα με την Άσκηση
, το οποίο σύμφωνα με την Άσκηση  (βλέπε ποστ
(βλέπε ποστ  ) ισούται με
) ισούται με 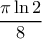 .
.

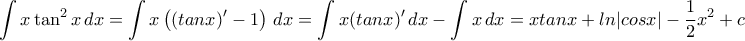
![\displaystyle{\int \dfrac {d x }{x+ \sqrt [3] x} \displaystyle{\int \dfrac {d x }{x+ \sqrt [3] x}](/forum/ext/geomar/texintegr/latexrender/pictures/4d8c3fa08dab094cf74a3fd5887a817d.png)
![\displaystyle{\begin{aligned}
\int \frac{\mathrm{d}x}{x+ \sqrt[3]{x}} &\overset{x=y^3}{=\! =\! =\! =\! =\!} \int \frac{3y^2}{y^3+y}\, \mathrm{d}y \\
&= \int \frac{3y^2}{y \left ( y^2+1 \right )} \, \mathrm{d}y \\
&= \int \frac{3y}{y^2+1} \, \mathrm{d}y\\
&=\frac{3}{2} \int \frac{\left ( y^2+1 \right )'}{y^2+1} \, \mathrm{d}y \\
&= \frac{3 \ln \left ( y^2+1 \right )}{2} \\
&= \frac{3 \ln \left ( \sqrt[3]{x^2} + 1 \right )}{2} + c \; , \; c \in \mathbb{R}
\end{aligned}} \displaystyle{\begin{aligned}
\int \frac{\mathrm{d}x}{x+ \sqrt[3]{x}} &\overset{x=y^3}{=\! =\! =\! =\! =\!} \int \frac{3y^2}{y^3+y}\, \mathrm{d}y \\
&= \int \frac{3y^2}{y \left ( y^2+1 \right )} \, \mathrm{d}y \\
&= \int \frac{3y}{y^2+1} \, \mathrm{d}y\\
&=\frac{3}{2} \int \frac{\left ( y^2+1 \right )'}{y^2+1} \, \mathrm{d}y \\
&= \frac{3 \ln \left ( y^2+1 \right )}{2} \\
&= \frac{3 \ln \left ( \sqrt[3]{x^2} + 1 \right )}{2} + c \; , \; c \in \mathbb{R}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/c9aeadff6e25066133adb54bd4d5dcaa.png)

![\displaystyle{\int \dfrac {d x }{\sqrt x+ \sqrt [3] x} \displaystyle{\int \dfrac {d x }{\sqrt x+ \sqrt [3] x}](/forum/ext/geomar/texintegr/latexrender/pictures/92269a63e7fbd19e1e163a99e5e19b05.png)
![\displaystyle{\begin{aligned}
\int \frac{\mathrm{d}x}{\sqrt{x} + \sqrt[3]{x}} &\overset{x=y^6}{=\! =\! =\! =\!} \int \frac{6y^5}{y^3 + y^2} \, \mathrm{d}y \\
&= \int \frac{6 y^5}{y^2 \left ( y + 1 \right )} \, \mathrm{d}y \\
&= \int \frac{6y^3}{y+1} \, \mathrm{d}y \\
&= 6 \int \left ( y^2 - y - \frac{1}{y+1} + 1 \right ) \, \mathrm{d}y \\
&= 2y^3 - 3y^2 - \ln (y+1) + 6y \\
&= 2 \sqrt{x} - 3 \sqrt[3]{x} - 6 \ln \left ( \sqrt[6]{x} + 1 \right ) + 6 \sqrt[6]{x} + c \; , \; c \in \mathbb{R}
\end{aligned}} \displaystyle{\begin{aligned}
\int \frac{\mathrm{d}x}{\sqrt{x} + \sqrt[3]{x}} &\overset{x=y^6}{=\! =\! =\! =\!} \int \frac{6y^5}{y^3 + y^2} \, \mathrm{d}y \\
&= \int \frac{6 y^5}{y^2 \left ( y + 1 \right )} \, \mathrm{d}y \\
&= \int \frac{6y^3}{y+1} \, \mathrm{d}y \\
&= 6 \int \left ( y^2 - y - \frac{1}{y+1} + 1 \right ) \, \mathrm{d}y \\
&= 2y^3 - 3y^2 - \ln (y+1) + 6y \\
&= 2 \sqrt{x} - 3 \sqrt[3]{x} - 6 \ln \left ( \sqrt[6]{x} + 1 \right ) + 6 \sqrt[6]{x} + c \; , \; c \in \mathbb{R}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/e7144203cd4fa773c7320a63eac798c2.png)
 .
. .
.  τον παρονομαστή. Ήδη είδαμε ότι ο αριθμητής είναι
τον παρονομαστή. Ήδη είδαμε ότι ο αριθμητής είναι  συν αυτό που μόλις έγραψα. Εύκολα τώρα βλέπουμε ότι, τελικά, ο αριθμητής ισούται με
συν αυτό που μόλις έγραψα. Εύκολα τώρα βλέπουμε ότι, τελικά, ο αριθμητής ισούται με  (εύκολο συγκρίνοντας συντελεστές). Δηλαδή θέλουμε να ολοκληρώσουμε την
(εύκολο συγκρίνοντας συντελεστές). Δηλαδή θέλουμε να ολοκληρώσουμε την  , που είναι άμεση. Δεν χρειάζεται να πληκτρολογήσω την μεγάλη παράσταση.
, που είναι άμεση. Δεν χρειάζεται να πληκτρολογήσω την μεγάλη παράσταση.


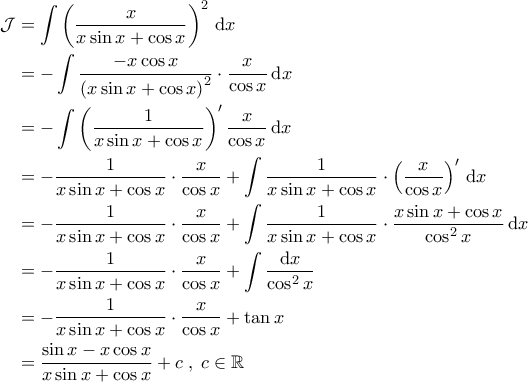
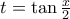 .
.
 , η οποία καθιστά την συνάρτηση συνεχή και το σύνολο τιμών της .
, η οποία καθιστά την συνάρτηση συνεχή και το σύνολο τιμών της . , για τον οποίο ισχύει :
, για τον οποίο ισχύει :  .
.
 (έκανα l' Hospital ή αλλιώς διαίρεσα αριθμητή και παρονομαστή δια
(έκανα l' Hospital ή αλλιώς διαίρεσα αριθμητή και παρονομαστή δια  ). Ο άλλος τρόπος είναι από το ανάπτυγμα
). Ο άλλος τρόπος είναι από το ανάπτυγμα  που είναι ήδη συνεχής, με τιμή
που είναι ήδη συνεχής, με τιμή  στο
στο  .
.  . Αν λοιπόν αυτό είναι ίσο με
. Αν λοιπόν αυτό είναι ίσο με  . Το μικρότερο θετικό τέτοιο
. Το μικρότερο θετικό τέτοιο  , δηλαδή
, δηλαδή 
 , επομένως
, επομένως  :
: 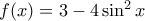 , απ' όπου προκύπτει άμεσα και το σύνολο
, απ' όπου προκύπτει άμεσα και το σύνολο ![[-1 , 3] [-1 , 3]](/forum/ext/geomar/texintegr/latexrender/pictures/6f0916000f0564088904f5fb31be5424.png) , τιμές που παίρνει στο
, τιμές που παίρνει στο 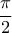 ...
...

 .
.
 είναι ειδική περίπτωση αυτής εδώ, με
είναι ειδική περίπτωση αυτής εδώ, με  . Αργότερα θα αναρτήσω μία ακόμα ποιο ουσιαστική γενίκευση που ξεκαθαρίζει το "τι τρέχει".
. Αργότερα θα αναρτήσω μία ακόμα ποιο ουσιαστική γενίκευση που ξεκαθαρίζει το "τι τρέχει".