Αφού το έπιασα , ας το τελειώσω κιόλας...Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 16, 2019 8:52 pmΣυμπλήρωμα της προηγούμενης:
Άσκηση 8β
Να υπολογισθεί το ολοκλήρωμα.
Εδώείναι το κλασματικό μέρος του
. Επιτρέπεται να χρησιμοποιήσετε αυτά που βρήκε ο Τόλης στο αμέσως προηγούμενο ποστ.
Λήμμα 1: Ισχύει ότι
 .
. Απόδειξη:
![\displaystyle{\begin{aligned}
\int_{\pi/3}^{2} \frac{\mathrm{d}x}{\sin x} &= \int_{\pi/3}^{2}\frac{\sin x}{\sin^2 x} \, \mathrm{d}x \\
&= \int_{\pi/3}^{2} \frac{\sin x}{1-\cos^2 x} \,\mathrm{d}x \ \\
&\!\!\!\!\!\overset{u=\cos x}{=\! =\! =\! =\!} -\int_{1/2}^{\cos 2} \frac{\mathrm{d}u}{1-u^2} \\
&= \int_{\cos 2}^{1/2} \frac{\mathrm{d}u}{1-u^2}\\
&= \frac{1}{2} \left [ \ln \left | u+1 \right | - \ln \left | u-1 \right | \right ]_{\cos 2}^{1/2} \\
&=\frac{1}{2} \left [ \ln \frac{3}{2} - \ln \frac{1}{2} - \ln \left | 1+\cos 2 \right | + \ln \left | \cos 2 -1 \right |\right ] \\
&= \frac{\ln 3}{2} + \frac{1}{2}\ln \left | \frac{\cos 2-1}{ 1+\cos 2} \right |\\
&= \frac{\ln 3}{2} + \frac{1}{2}\ln \left | -\tan^2 1 \right | \\
&=\frac{\ln 3}{2} + \ln \tan 1
\end{aligned}} \displaystyle{\begin{aligned}
\int_{\pi/3}^{2} \frac{\mathrm{d}x}{\sin x} &= \int_{\pi/3}^{2}\frac{\sin x}{\sin^2 x} \, \mathrm{d}x \\
&= \int_{\pi/3}^{2} \frac{\sin x}{1-\cos^2 x} \,\mathrm{d}x \ \\
&\!\!\!\!\!\overset{u=\cos x}{=\! =\! =\! =\!} -\int_{1/2}^{\cos 2} \frac{\mathrm{d}u}{1-u^2} \\
&= \int_{\cos 2}^{1/2} \frac{\mathrm{d}u}{1-u^2}\\
&= \frac{1}{2} \left [ \ln \left | u+1 \right | - \ln \left | u-1 \right | \right ]_{\cos 2}^{1/2} \\
&=\frac{1}{2} \left [ \ln \frac{3}{2} - \ln \frac{1}{2} - \ln \left | 1+\cos 2 \right | + \ln \left | \cos 2 -1 \right |\right ] \\
&= \frac{\ln 3}{2} + \frac{1}{2}\ln \left | \frac{\cos 2-1}{ 1+\cos 2} \right |\\
&= \frac{\ln 3}{2} + \frac{1}{2}\ln \left | -\tan^2 1 \right | \\
&=\frac{\ln 3}{2} + \ln \tan 1
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/10ad26dbac2c3452c657f158a8adcfc6.png)
Λήμμα 2: Ισχύει ότι
 .
. Απόδειξη: Έπεται από το γεγονός ότι:

Οπότε για το αρχικό ολοκλήρωμα έχουμε,

Επόμενη άσκηση παρακαλώ.


 .
. το ζητούμενο ολοκλήρωμα. Τότε:
το ζητούμενο ολοκλήρωμα. Τότε: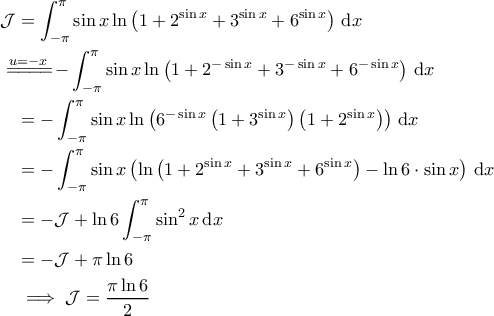

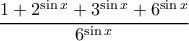 , και λοιπά.
, και λοιπά.
 γνωστό. Και λοιπά.
γνωστό. Και λοιπά.
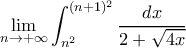



![\lim_{n\rightarrow +\infty }\int_{n^2}^{(n+1)^2}\dfrac{1}{2+\sqrt{4x}}dx=\lim_{n\rightarrow +\infty }[\sqrt{x}-ln(1+\sqrt{x})]_{_{n^2}} ^{(n+1)^2}
=\lim_{n\rightarrow +\infty }(1-ln(n+2)+ln(n+1))= \lim_{n\rightarrow +\infty }[1-ln(\dfrac{n+2}{n+1})]=\lim_{n\rightarrow +\infty }[1-ln(1+\dfrac{1}{n+1})]=1-ln1=1 \lim_{n\rightarrow +\infty }\int_{n^2}^{(n+1)^2}\dfrac{1}{2+\sqrt{4x}}dx=\lim_{n\rightarrow +\infty }[\sqrt{x}-ln(1+\sqrt{x})]_{_{n^2}} ^{(n+1)^2}
=\lim_{n\rightarrow +\infty }(1-ln(n+2)+ln(n+1))= \lim_{n\rightarrow +\infty }[1-ln(\dfrac{n+2}{n+1})]=\lim_{n\rightarrow +\infty }[1-ln(1+\dfrac{1}{n+1})]=1-ln1=1](/forum/ext/geomar/texintegr/latexrender/pictures/8121372dac7f20bd9cc74bc42c8a7601.png)
 , οπότε
, οπότε 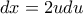 και έχουμε:
και έχουμε:  .
.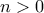 βρίσκουμε:
βρίσκουμε:  , οπότε
, οπότε  .
.


 . Βρείτε εκείνη την παράγουσα
. Βρείτε εκείνη την παράγουσα  της
της 
 είναι
είναι  . Ποια είναι τα κοινά σημεία των
. Ποια είναι τα κοινά σημεία των  ;
;

 οπότε έχουμε, αν
οπότε έχουμε, αν 
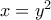 και με κατά παράγοντες έχουμε
και με κατά παράγοντες έχουμε 
 . Για τα κοινά σημεία θέλουμε
. Για τα κοινά σημεία θέλουμε  , ισοδύναμα
, ισοδύναμα  . Λύνοντας, την
. Λύνοντας, την  η θετική ρίζα είναι
η θετική ρίζα είναι  , οπότε
, οπότε  .
.
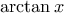 είναι εκτός σχολικής ύλης. Την τοποθετώ μόνο και μόνο γιατί είναι το δίδυμο αδελφάκι της Άσκησης 12. Το μόνο που χρειάζεται να ξέρεις για την
είναι εκτός σχολικής ύλης. Την τοποθετώ μόνο και μόνο γιατί είναι το δίδυμο αδελφάκι της Άσκησης 12. Το μόνο που χρειάζεται να ξέρεις για την  είναι ότι
είναι ότι 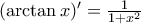 .
.![\displaystyle{\begin{aligned}
\int_{0}^{1}\frac{\arctan x}{1+x}\, \mathrm{d}x &= \left [ \ln(x+1) \arctan x \right ]_0^1 - \int_{0}^{1} \frac{\ln(1+x)}{1+x^2}\, \mathrm{d}x\\
&=\frac{\pi \ln 2}{4} - \int_{0}^{1}\frac{\ln(1+x)}{1+x^2}\, \mathrm{d}x \\
&=\frac{\pi \ln 2}{4}- \frac{\pi \ln 2}{8} \\
&= \frac{\pi \ln 2}{8}
\end{aligned}} \displaystyle{\begin{aligned}
\int_{0}^{1}\frac{\arctan x}{1+x}\, \mathrm{d}x &= \left [ \ln(x+1) \arctan x \right ]_0^1 - \int_{0}^{1} \frac{\ln(1+x)}{1+x^2}\, \mathrm{d}x\\
&=\frac{\pi \ln 2}{4} - \int_{0}^{1}\frac{\ln(1+x)}{1+x^2}\, \mathrm{d}x \\
&=\frac{\pi \ln 2}{4}- \frac{\pi \ln 2}{8} \\
&= \frac{\pi \ln 2}{8}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/1a32d167727f3a6091aff7194af1e418.png)