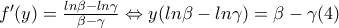Θα ήθελα μια επιβεβαίωση στα παρακάτω ολοκληρώματα.στην επανάληψη μου λύνω απο ένα άλλο βοηθητικό κ' έχω βρει αλλά αποτελέσματα σε σχέση με αυτά που δείχνει πίσω στις λύσεις .

Το οποίο έβγαλα ως αποτέλεσμα :
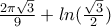

Το οποίο το έβαλα ,
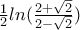

Όπου βγάζω το ίδιο αποτέλεσμα με το προηγούμενο ολοκλήρωμα
Και στα 3 βγάζω διαφορετικό αποτέλεσμα από το βοηθητικό
Θα ήθελα επίσης να μου λύσει και ποιος και μου την γράψει όσο πιο καλά και κατανοητά μπορεί είναι από το ίδιο βοηθητικό και δεν καταλαβαίνω ούτε την λύση που δίνει πίσω , είναι στην ασκησιολογια του θμτ .Θέτει γ= α+β/2 και δεν καταλαβαίνω πως προκύπτουν αυτά που γράφει
Να δείξετε ότι υπάρχουν
 . τέτοια ώστε
. τέτοια ώστε 
Καταλάβαινω ότι το mathematica δεν είναι λυσάρι απλός πλησιάζει ο καιρός για τις εξετάσεις και θα ήθελα να ξεμπερδευω με κάποια πράγματα
Ευχαριστώ εκ των προτέρων για όποιον βρει χρόνο να με βοηθήσει


 Με
Με  .
.
 Είναι το ίδιο.
Είναι το ίδιο.
 να είναι
να είναι  αφού
αφού 
 τότε
τότε 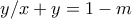 με
με 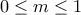 αφού
αφού 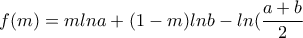 τότε
τότε 
 εχει ρίζα στο
εχει ρίζα στο  συνεπώς ισχύει το ζητούμενο
συνεπώς ισχύει το ζητούμενο τότε
τότε  τότε
τότε  που παίρνουμε από τον Bolzano
που παίρνουμε από τον Bolzano 
 τέτοια ώστε
τέτοια ώστε 




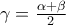 οποτε
οποτε 




![[\alpha ,\gamma ] [\alpha ,\gamma ]](/forum/ext/geomar/texintegr/latexrender/pictures/34db1f721e79d259415f8cfbcb95ad94.png) κ στο
κ στο ![[\gamma,\beta] [\gamma,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/f137e1925d78892a809d5f9a7b37dba4.png)