 παραγωγίσιμη στο
παραγωγίσιμη στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) με
με  για κάθε
για κάθε 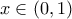 να δείξετε ότι ισχύει:
να δείξετε ότι ισχύει:
Να ερμηνευτεί γεωμετρικά το αποτέλεσμα.
Συντονιστής: R BORIS
 παραγωγίσιμη στο
παραγωγίσιμη στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) με
με  για κάθε
για κάθε 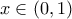 να δείξετε ότι ισχύει:
να δείξετε ότι ισχύει:
...μια γρήγορη αντιμετώπιση...Λάμπρος Κατσάπας έγραψε: ↑Τετ Απρ 04, 2018 8:29 amΓια κάθε συνάρτησηπαραγωγίσιμη στο
με
για κάθε
να δείξετε ότι ισχύει:

Να ερμηνευτεί γεωμετρικά το αποτέλεσμα.
 οπότε
οπότε  (1)και
(1)και  (2)
(2) 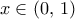 υπάρχουν
υπάρχουν  ώστε
ώστε  και
και 
 με την ισότητες να ισχύουν για
με την ισότητες να ισχύουν για 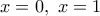 απ όπου
απ όπου  και
και 

 (1)
(1) ![-x+f(0)\le f(x)\le x+f(0),\,\,x\in [0,\,1] -x+f(0)\le f(x)\le x+f(0),\,\,x\in [0,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/9bd9dd8a59d9f675fe0d98c512dc280b.png) προκύπτει ότι
προκύπτει ότι  ισοδύναμα
ισοδύναμα  (2)
(2) 

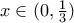 υπάρχει
υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε .
. υπάρχει
υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε .
. υπάρχει
υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες