Ισότητα και εμβαδόν

#1

Χρόνια πολλά σε όλους

Να αποδείξετε ότι : $\displaystyle \int\limits_{0}^{1}{{{e}^{-{{x}^{2}}}}}dx+\int\limits_{1}^{1/e}{\sqrt{\ln \left( \frac{1}{x} \right)}dx=\frac{1}{e}}$
Δώστε και μια γεωμετρική ερμηνεία και ένα σχήμα .

#2

exdx έγραψε: ↑
Τρί Ιαν 02, 2018 10:30 am
Χρόνια πολλά σε όλους

Να αποδείξετε ότι : $\displaystyle \int\limits_{0}^{1}{{{e}^{-{{x}^{2}}}}}dx+\int\limits_{1}^{1/e}{\sqrt{\ln \left( \frac{1}{x} \right)}dx=\frac{1}{e}}$
Δώστε και μια γεωμετρική ερμηνεία και ένα σχήμα .

...Καλημέρα

και καλή χρονιά σε όλους

Θεωρώντας την συνάρτηση $f(x)={{e}^{-{{x}^{2}}}},\,\,x\in [0,\,1]$ αυτή είναι παραγωγίσιμη με

${f}'(x)=-2x{{e}^{-{{x}^{2}}}}<,\,\,x\in (0,\,1)$ άρα γνήσια φθίνουσα στο $[0,\,1]$ , επομένως και '1-1'

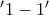άρα αντιστρέψιμη με

${{f}^{-1}}:f([0,\,1])\to [0,\,1]$ και $f([0,\,1])=[f(1),\,f(0)]=[\frac{1}{e},\,1]$ έτσι ${{f}^{-1}}:[\frac{1}{e},\,1])\to [0,\,1]$

και τύπο που προκύπτει από την επίλυση της εξίσωσης $f(x)=y\Leftrightarrow {{e}^{-{{x}^{2}}}}=y,\,\,x\in [0,\,1]$ και $y\in [\frac{1}{e},\,1]$

που ισοδύναμα έχουμε $\ln {{e}^{-{{x}^{2}}}}=\ln y\Leftrightarrow -{{x}^{2}}=\ln y\Leftrightarrow {{x}^{2}}=-\ln y\Leftrightarrow$

${{x}^{2}}=\ln {{y}^{-1}}\Leftrightarrow x=\sqrt{\ln \frac{1}{y}}={{f}^{-1}}(y)$

${{f}^{-1}}(x)=\sqrt{\ln \frac{1}{x}},\,\,\,x\in [\frac{1}{e},\,1]$ και τότε το ζητούμενο γίνεται $\int\limits_{0}^{1}{f(x)}dx+\int\limits_{f(0)}^{f(1)}{{{f}^{-1}}(x)dx=\frac{1}{e}}$ (1)

Τώρα αν ${{f}^{-1}}(x)=u\Leftrightarrow x=f(u)$ και dx={f}'(u)du

με $x=f(1)\to u=1,\,\,\,x=f(0)\to u=0$ έχουμε

$\int\limits_{f(0)}^{f(1)}{{{f}^{-1}}(x)dx=\int\limits_{0}^{1}{u{f}'(u)du=\left[ uf(u) \right]_{0}^{1}-}}\int\limits_{0}^{1}{f(u)du}\Leftrightarrow$
$\displaystyle \int\limits_{0}^{1}{f(u)du}+\int\limits_{f(0)}^{f(1)}{{{f}^{-1}}(x)dx=f(1)}=\frac{1}{e}$ που είναι αυτό που θέλαμε...

...έτοιμο και το σχήμα..

: ΙΣΟΤΗΤΑ ΜΕ ΕΜΒΑΔΟ.jpg (22.19 KiB) Προβλήθηκε 846 φορές

Τώρα σύμφωνα με το σχήμα το άθροισμα $\int\limits_{0}^{1}{f(x)}dx+\int\limits_{f(0)}^{f(1)}{{{f}^{-1}}(x)dx=}\int\limits_{0}^{1}{f(x)}dx-\int\limits_{f(1)}^{f(0)}{{{f}^{-1}}(x)dx}$

δηλαδή είναι το εμβαδό του χωρίου μεταξύ της ${{C}_{f}},\,\,{x}'x,\,x=0,\,\,x=1$ δηλαδή του χωρίου ABOZ

μείον το εμβαδό του χωρίου

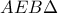μεταξύ της ${{C}_{{{f}^{-1}}}},\,\,{x}'x,\,x=\frac{1}{e},\,\,x=1$ δηλαδή του χωρίου $AEB\Delta$ που λόγω συμμετρίας ως προς την y=x

είναι ίσο με το εμβαδό του χωρίου ΑΓΖ που δίνει το εμβαδό του ορθογωνίου $AB{\mathrm O}\Gamma$

που είναι ίσο με $({\mathrm O}\Beta )({\mathrm O}\Gamma )=1\,\frac{1}{e}=\frac{1}{e}$

Φιλικά και Μαθηματικά
Βασίλης

Ισότητα και εμβαδόν

Ισότητα και εμβαδόν

Re: Ισότητα και εμβαδόν

Μέλη σε σύνδεση