
Με αφορμή το Γ4_2017
Συντονιστής: R BORIS
-
Grosrouvre
- Δημοσιεύσεις: 296
- Εγγραφή: Τρί Ιούλ 15, 2014 11:37 pm
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13298
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Με αφορμή το Γ4_2017
Αλλιώς. Έστω ![\displaystyle{f(x) = \frac{{\sin x}}{x},x \in \left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}. \displaystyle{f(x) = \frac{{\sin x}}{x},x \in \left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}.](/forum/ext/geomar/texintegr/latexrender/pictures/0f4e2b9f32d5e7777c7917aebfff3e56.png) Είναι
Είναι 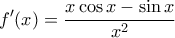
Θέτω και είναι
και είναι  άρα η
άρα η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]} \displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ca9d4beefae596c9073fc5b1462e5b03.png)
απ' όπου εύκολα προκύπτει ότι στο ίδιο διάστημα, οπότε και η
στο ίδιο διάστημα, οπότε και η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]} \displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ca9d4beefae596c9073fc5b1462e5b03.png)

![\displaystyle{f(x) = \frac{{\sin x}}{x},x \in \left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}. \displaystyle{f(x) = \frac{{\sin x}}{x},x \in \left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}.](/forum/ext/geomar/texintegr/latexrender/pictures/0f4e2b9f32d5e7777c7917aebfff3e56.png) Είναι
Είναι 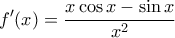
Θέτω
 και είναι
και είναι  άρα η
άρα η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]} \displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ca9d4beefae596c9073fc5b1462e5b03.png)
απ' όπου εύκολα προκύπτει ότι
 στο ίδιο διάστημα, οπότε και η
στο ίδιο διάστημα, οπότε και η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![\displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]} \displaystyle{\left[ {\frac{\pi }{4},\frac{\pi }{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/ca9d4beefae596c9073fc5b1462e5b03.png)

Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες

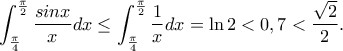
 δείτε, π.χ.
δείτε, π.χ. 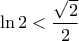 προκύπτει και από την
προκύπτει και από την  για
για 